船舶推进轴系冲击建模和仿真研究

2012-01-22，，，

船海工程 2012年2期

，，，

(中国舰船研究设计中心，武汉 430064)

船舶推进轴系包括主机输出端推力轴承与螺旋桨之间的传动轴以及轴系附属设备。船舶轴系设备冲击响应是指轴系及附属设备的冲击强度、刚度问题，即冲击作为一种动载荷对推进轴系及轴系附属设备材料的破坏，主要涉及材料刚度失效(大变形)和强度失效(材料进入塑性屈服阶段或断裂)两种形式。推进轴系的抗冲击能力直接关系到船舶动力系统的生存能力，但由于推进轴系结构尺寸大，附属设备多，几乎无法完成实船冲击实验，根据船舶建造规范-冲击安全性要求，对于不能做冲击试验或爆炸试验的冲击安全A和B级的设备应该进行冲击计算，冲击计算要验证设备本身和设备支撑位置(基座、局部甲板和舱壁、动力的输入部位等)承受冲击的能力。所以本文采用有限元法，建立船舶推进轴系冲击模型，使用加速度为冲击输入条件下，完成推进轴系抗冲击仿真计算研究，为推进轴系抗冲击计算提供一种计算思路[1]。

1 推进轴系有限元建模

为保证推进轴系有限元分析的准确性，在建模时将轴系及附属设备均按实际结构进行建模，另一方面为节约有限元仿真计算时间，需要对于局部结构进行有效的简化。

其中轴系基本参数为轴系长度约65 m；中间轴段直径约410 mm；螺旋桨轴直径约510 mm；轴段材料屈服极限580 MPa；螺旋桨简化为均质圆盘，其质量约12 000 kg。

根据实船情况，对轴系及其附属设备模型简化如下。

1)简化模型中倒角、孔、键槽以及阶梯过渡部位。

2)简化推力轴承、中间轴承等外连的油管路、水管路和质量较轻的端盖等。

3)简化紧固件采用螺栓孔内部所有节点刚性连接的处理方式。

4)简化轴承轴瓦与轴颈的连接处理，轴颈-轴瓦之间的非线性“接触”关系以线性连接关系替代，另外由于冲击作用时间较短，所以又认为接触之前的油膜阻尼力耗功可以忽略，忽略油膜力的作用，假设轴颈和轴瓦为一种纯接触关系，两者之间的间隙通过ANSYS 软件接触计算模块功能调整为零。

5)简化推力轴承推力块与平衡块、平衡块与套环之间连接的“接触”模型，“推进轴-推力块-平衡块-套环”子系统采用“接触”连接模型。

有限元模型网格划分采用六面体单元和四面体单元相结合，使得有限元分析具有较高的精度和较少的单元和节点总数；在结构复杂的零件上使用四面体网格进行划分，但是为了保证有限元仿真计算的准确性，应将细化网格单元比例控制在一定范围内。有限元网格尺寸和质量的划分情况如下。

平均单元尺寸为20 mm，最小尺寸5 mm，实体单元采用solid45单元，弹簧单元采用combin14单元，接触单元contact173和target170。

单元采用六面体结构，四面体单元数≤6%，除结构外，不允许有两个以上的四面体单元连在一起。不能出现奇数节点孔，孔周围尽量不出现三角形单元。推进轴系有限元模型及边界处理见图1～3。

图1 轴承轴瓦与轴颈线性连接方式

图2 轴段有限元模型

图3 螺旋桨轴有限元模型

2 冲击计算边界输入

冲击仿真计算是“固定基础”的运动(冲击激发)导致系统的响应，对于推进轴系来说，冲击响应计算首先得确定其“固定基础”，即所有与设备相连但没有被包含该设备冲击动力学模型部分的部件与该设备的分界界面，所有界面的刚性连接即为“固定基础”，由于整个推进轴系为一个位置跨度大的系统，所以，固定基础每一处激励均相等的基本假设不适合推进轴系，所以本文将整个推进轴系沿轴向分成几个部分，从而将推进轴系冲击计算转换为分段冲击计算。

(1)

(2)

(3)

令y(t)=x(t)-u，则有

(4)

(5)

(6)

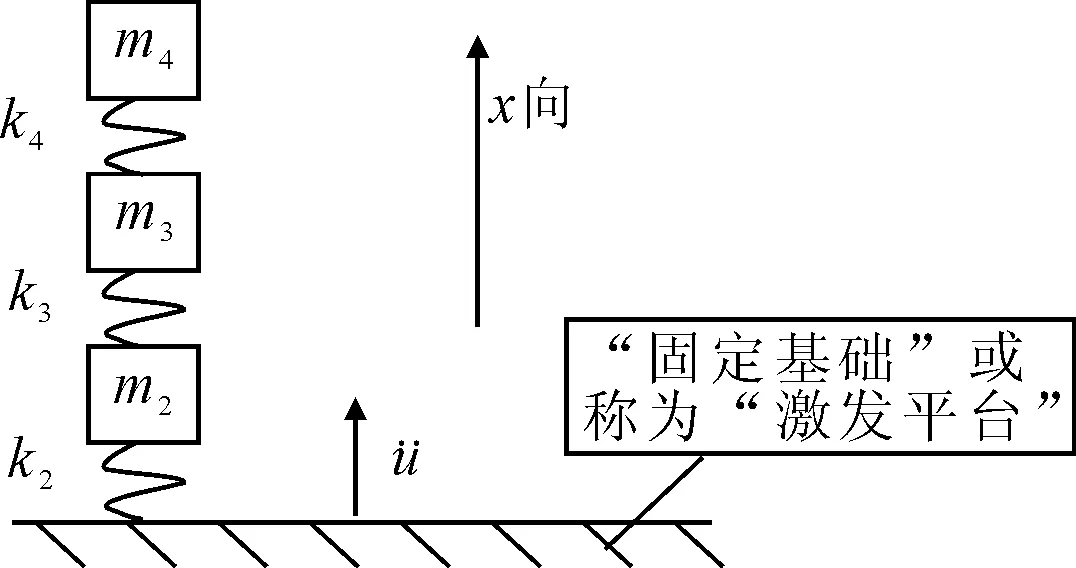
图4 三质量系统基础冲击模型

从基础冲击激励下系统的动力学方程可以看出，基础加速度冲击激励实际上等效于施加在各质量点上。求解以上公式即可得到各质量点的位移、速度和加速度响应时间历程。而系统应力即弹簧弹性力为k2y2、k3(y3-y2)、k4(y3-y4)。基础加速度运动激励实际上是施加在系统各质量点上，而系统在界面与“激发平台”固接。进而延伸到有限元离散系统中， ANSYS软件进行瞬态响应计算时，基础加速度运动冲击激励施加在“Global”单元即所有单元体上，而系统在“固定基础”处六个自由度全约束[2]。

根据冲击标准BV0430，选冲击设计输入激励选择组合双三角波加速度时间历程曲线，见图5。