潜艇肋骨初挠度计算研究

(海军驻渤海造船厂军事代表室，辽宁 葫芦岛 125004)

潜艇的耐压船体是保证潜艇和人员安全的关键部件，因而耐压船体的设计与制造受到人们的特别关注与重视。耐压船体的肋骨又是保证耐压船体结构强度与稳定的关键部件。肋骨初挠度对耐压船体结构的稳定性影响很大，故各国对肋骨初挠度都有很严格的控制。一般都不是直接控制肋骨的初挠度的测量值，而对肋骨初挠度的计算值进行控制。我国现行潜艇设计规范(以下简称《规范》)，也是对肋骨初挠度的计算值进行控制。尽管规范对肋骨初挠度的计算规定了一套计算方法，但在实施计算过程中还会遇到一些问题。例如当肋骨的某个测点被液舱或基座遮挡，无法测量需要沿圆周移位时带来的误差会多少？计算出来的拟合圆能否再平移？当可拆板的板缝不在测点上，而该处的变形又比较大时如何计算板缝处的初挠度等。搜索国内研究文献未见相关的报道。

本文主要对潜艇肋骨初挠度的换算方法进行研究，研究在测点的间距不等时或增多测点时如何对肋骨初挠度进行正确的换算[1-3]。

1 规范对肋骨初挠度换算的方法

1.1 肋骨的实际形状与理想圆的径向偏差

《规范》认为在以测量中心为坐标原点的坐标系中，肋骨的实际形状可以用函数R(α)表示，与肋骨实际形状最接近的理想圆可用函数R0(α)表示。肋骨的实际形状与理想圆的径向差可用函数W(α)表示。如果理想圆的圆心与坐标原点的距离与理想圆的半径相比非常小，则函数R0(α)的方程可表示为

R0(α)=R+asinα+bcosα

(1)

式中：R——理想圆的半径；

a——理想圆的圆心与坐标原点的距离向y轴的投影值；

b——理想圆的圆心与坐标原点的距离向x轴的投影值;

α——某测量点与x轴的夹角。

肋骨的实际形状与理想圆的径向差可表示为

W(α)=R(α)-R-asinα-bcosα

(2)

1.2 与肋骨实际形状最接近的理想圆的确定

《规范》认为与肋骨实际形状最接近的理想圆可借助数学上的最小二乘法原理来确定。肋骨实际形状相对于任何一个圆的偏差平方和是不一样的，某一个满足偏差平方和为最小的圆就是与肋骨实际形状最接近的理想圆。由于肋骨圆周上有无数的点，所以要计算每一点的偏差平方和就必须用到积分，用数学公式表示为

(3)

由式(2)可见，对一特定的肋骨形状R(α)为已知值，待定的变量为R、a及b，对各待定变量求偏导后等于零可得

(4)

(5)

(6)

《规范》采用表格计算法来最后求得肋骨径向偏差，在表格计算中规定了每个测点的正弦与余弦值，故测点的位置是固定的，不能左右移动，否则有些积分就不会为零，有些公共项就不能从积分中提出，总之会对理想圆的确定产生一些误差，另外如果测点数增加，则计算表格必须作相应修改。在实际使用中会经常遇到增加测点或测点间距不均匀的事件，这时原有的计算表格就不再适用了。

2 本文对肋骨初挠度换算的方法

由于《规范》对肋骨初挠度的换算方法提出的时间较早，那时计算机还没有普及，所以采用表格计算方法，带有一定的限制条件。现在计算机已大大普及，所以完全可以不用表格计算方法。还是从最小二乘法原理出发，直接计算每一个测点的偏差平方和，再求该平方和最小值。即使每个测点间的距离不相等也无关紧要，也不受测点多少的限制及测量区域的限制。例如可以先设定一个理想圆的圆心位置及理想圆的半径，根据测点的坐标位置及理想圆圆心的坐标位置求出测点到理想圆圆心的距离再减去理想圆的半径就得到该测点的偏差，以此类推可计算出所有测点的偏差平方和。用步长来调整理想圆圆心的位置及半径的大小求该偏差平方和的最小值。即使用最简单的循环语句的算法也用不了多少时间就可确定理想圆圆心的位置及半径。每个测点的偏差可写成

(7)

式中：αi——每个测点与x轴的夹角。

所有测点偏差平方和可写成

(8)

当最小偏差平方和的理想圆圆心的坐标位置及半径求出后，再代入式(7)就可求得每个测点的偏差。

3 本文换算方法与规范表格计算的算例对比

3.1 均布32点肋骨测点算例

设某潜艇耐压体的半径为3 800 mm，采用32点均布肋骨测点，根据肋骨圆周初始测量值分别采用规范表格计算及本文方法求肋骨径向偏差。计算结果见表1、图1。从表1、图1的计算结果可以看出理想圆的坐标位置完全一样，理想圆的半径略有微小差别，各测点的径向偏差也非常接近，几乎完全重合。

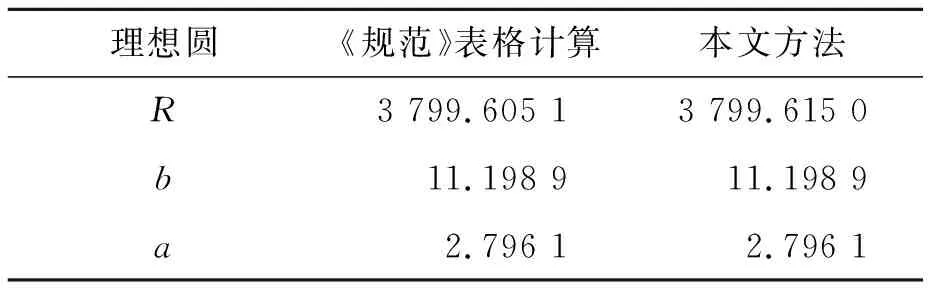
表1 两种方法之理想圆比较 mm

图1 两种方法之肋骨偏差值比较

3.2 不等间距32点肋骨测点算例

设某潜艇耐压体的半径为3 800 mm，采用32点肋骨测点，其中有个别测点与正常测点位置有偏移(2点与1点的夹角为9.77°，3点与2点的夹角为12.73°，30点与29点的夹角为12.73°、31点与30点的夹角为9.77°，其余测点间的夹角为11.25°)，肋骨圆周初始测量值与上例一样，分别采用规范表格计算及本文方法求肋骨径向偏差。《规范》方法1是不计测点2、3及30、31的位置偏移，计算中按均布看待，相当于将测点移位。《规范》方法2是考虑测点2、3及30、31的位置偏移，在计算表格中用测点的实际位置的角度值代入，但不修改表格计算方法。计算结果见表2、图2。从表2的计算结果可以看出《规范》方法1与本文方法的理想圆坐标位置完全一样，《规范》方法2与本文方法的理想圆坐标位置略有差别，从图2的计算结果可以看出《规范》方法1、《规范》方法2与本文方法的肋骨径向偏差重合度较好，个别点略有差别，例如最大偏差值都在测点20，但值不同，其中以本文方法的值最大为12.437 8，规范方法1的值最小为12.427 5，规范方法2的值为12.428 2。测点位置偏移不超过测点距离的1/3时，其误差在工程误差之内，可以接受。

表2 三种方法之理想圆比较 mm

图2 三种方法之肋骨偏差值比较

3.3 有可拆板时肋骨测点算例

设某潜艇耐压体的肋骨半径为3 800 mm，采用32点肋骨测点，在测点2、3之间及测点31、32之间有可拆板缝。该肋骨剖面见图3。

图3 肋骨有可拆板时测点图

有的单位对该肋骨偏差计算时还是采用规范的表格，但是增加了测点，同时将新增测点的sinα、cosα值代入表格，其它公式保持不变。这种方法的错误之处在于：①测点距离不均布，最小距离与最大距离相差较大，在求积分时不能提取角度的公共项；②测点的数量改变后对计算公式中的系数应作相应修改。本文称上述方法为方法1。方法2采用32点标准测点计算出理想圆后再根据可拆板缝左右的点2.1、2.2、31.1、31.2的测量值代入式(2)求出板缝左右点的偏差值。方法3采用本文方法计算36个测点的理想圆，再求每一测点的偏差。计算结果见表3、图4。从表3、图4的计算结果可以看出方法1与后两种方法的理想圆坐标值及半径值及测点的偏差都有一些较

大的差别。本文认为后两种方法都是正确的换算方法，虽然36点方法可直接得出板缝区的偏差，但从全船肋骨使用相同测点求出理想圆的角度出发，本文推荐采用32点计算法。

表3 有可拆板时3种方法之理想圆比较 mm

图4 有可拆板时3种方法之偏差值比较

4 结束语

1)本文方法与《规范》表格计算都是基于同一原理对测点的初挠度换算，两者的结果几乎完全一致，说明本文方法可以作为与规范表格计算并存的肋骨初挠度换算方法，本文方法与规范表格计算相比具有计算方法简单、计算结果正确、不受测点数量限制及测点距离是否均布的限制，当测点数量改变时或测点距离不均布时不用修改计算公式及计算方法，无论是整圆测点或非整圆测点都可用本文方法进行测点的初挠度换算；

2)当测点位置偏移不超过测点距离的1/3时，其误差在工程误差之内，可以接受；

3)对于拟合圆能否再平移问题，由于拟合圆平移后不能满足偏差平方和为最小，故拟合圆不能人为移动。

[1] 许缉平.潜艇强度[M].北京：国防工业出版社，1980.

[2] 张 菊,赵永东,张炳喜,等.耐压壳非圆度偏差检测研究[J].船舶工程,2005,27(4)：16-18.

[3] 李 忠,郭日修,贺小型.具有初始挠度的环肋圆柱壳在静水外压作用下的应力分析[J].中国造船,1987,28(2)：63-71.