艉轴承等效支点位置对轴系回旋振动的影响

(海军工程大学 科研部，武汉 4300333)

伴随着船舶大型化及推进功率的不断提高，推进系统倾向布置多轴系，增大舷外托架支承和艉管轴承间距等方式，结果使得轴系，尤其是高速船舶轴系的回旋振动固有频率降低，导致作用在螺旋桨上流体的频率有可能接近其回旋振动的固有频率，产生共振。因此探讨艉轴不同支承方式及其等效支点位置对轴系回旋振动的影响，对于优化轴系设计，防止推进轴系共振具有理论意义和工程应用价值[1]。

轴系回旋振动是由于轴系转动部件的不平衡以及螺旋桨在不均匀流场中所产生的交变弯矩引起的周期性弯曲现象。对于民用商船，螺旋桨转速通常较低(100～200 r/min)，而回旋振动的一阶固有频率较高(500～600 r/min以上)，在工作范围内一般不会出现共振问题，但对于舰艇推进轴系(尤其是高速船舶轴系)，则有可能发生[2]。

轴系回旋振动与艉轴承支点位置有关，各国船级社一般都是按照经验值加以确定[3]。实践表明，在轴系校中和回旋振动计算时，同种材料的轴系支点位置的变化范围常不一致，为此，ABS制定了艉轴承单点和双点支承规范，推荐采用两点支承，但两点的计算结果必须符合单点支承计算结果[4]。文献[5]运用传递矩阵研究船舶艉轴承刚性多支承问题对各轴承支反力分布的影响。文献[6]应用有限元方法对比研究了艉轴承单点和双点支承下轴系的振动特性，得到两点支承有更高的回旋振动固有频率。

目前，在分析回旋振动特性时，很少考虑艉轴承支点位置变动对各轴承受力状况及轴系回旋振动的影响，没有提出合适的轴承等效支点位置的确定方法。

本文以高速客船推进轴系为研究对象，将艉轴承支承分为单点支承、多点支承、分布支承及接触支承等四种方式，应用有限元方法，分别对轴系进行回旋振动建模，求取不同支承方式的轴承支反力、等效支点位置，以及回旋振动模态，探索支点位置对回旋振动的影响。

1 高速客船推进轴系组成

高速客船轴系主要由螺旋桨、艉轴、后艉轴承、中间艉轴承、前艉轴承和推力轴承等组成。后艉轴承、中间艉轴承为托架安装方式；推力轴承安装在主机内，没有推力轴。从螺旋桨艉端至曲轴倒数第一个主轴承，全长共8.146 9 m，见图1所示。后艉轴承、中间艉轴承、前艉轴承采用橡胶材料，结构尺寸见图2。轴承及轴颈材料属性见表1。该高速船推进轴系的相关数据如下。

主机型号： CUMMINS KAT50-M2

主机额定功率：1 398 kW

主机额定转速：1 950 r/min

螺旋桨桨叶数：5

螺旋桨额定转速：642 r/min

螺旋桨直径D：1.3 m

艉轴轴径：140 mm

图1 高速船舶轴系示意(单位：m)

图2 后艉托架轴实际尺寸

表1 轴承及轴颈材料属性

艉轴承材料：橡胶轴承

艉轴承长径比：4∶1

螺旋桨空气中质量m′：349.0 kg

螺旋桨附水质量m：410.5 kg

螺旋桨极转动惯量(附水)：33.8 kg·m2

螺旋桨径向转动惯量(附水)：20.8 kg·m2

螺旋桨附连水质量系数为1.18，极转动惯量附连水系数为1.30，径向转动惯量附连水系数为1.60。

2 艉轴承支承方式

在计算回旋振动时，应考虑轴承支点方式的影响，如单点支承、两点支承、分布支承、接触支承。一般常用单点支承。

1)单点支承。按有关规定，轴系回旋振动计算时，橡胶轴承的支点位置离该轴承后端面为(1/3～1/2)Lb,式中：Lb为后艉轴承轴衬长度。这种单点支承位置的选取是一般凭经验，但争议颇多。

3)分布支承。分布支承方式考虑了轴承单元对轴段单元的弯矩效果，从矩阵角度看，类似于分布质量。分布式支承

(1)

式中：kxx——轴向单位长度刚度。

4)接触支承。选取面-面接触类型进行艉轴承的实体接触分析，能较好地模拟轴颈与轴承的实际接触情况。

3 艉轴承实体模型

图3为轴系与艉轴承有限元模型。

图3 轴系与艉轴承有限元分析模型

艉轴与艉轴承相配合段为实体单元，其他轴段采用梁单元。实体只有3个平动自由度，梁单元具有3个平动和3个转动自由度。梁与实体连接处出现的自由度不统一，采用多点约束(MPC)处理单元，解决了不同单元载荷传递及变形不协调问题。

4 不同支承方式的轴承静态支点

4.1 等效支点的确定

通过不同支承方式的轴承受力分布,确定等效支点位置，及其对回旋振动模态的影响规律，从而确定不同支承方式的合理性。

1)两点支承及分布支承。两点支承及分布支承的等效支点位置计算方法相同，两点支承及分布支承都是将艉轴架轴承沿轴向简化为多个点支承，并将每个支点(包括等效支点)的支反力分别对艉轴承后端面取矩，得出等效支点位置。

X=∑(Fi·Xi)/∑Fi

(2)

式中：Fi——第i个支点的支反力；

X——等效支点距艉轴架轴承后端面距离；

Xi——第i个支点距艉轴架轴承后端面距离。

2)接触支承。等效支点位置X的确定，是将每个单元的接触压力垂向分力与相应单元的面积和单元形心的相应坐标相乘，然后除以相应单元的垂向接触力与该单元形心相应坐标的乘积，即

X=∑(Pi·Ai·Xi)/∑(Pi·Ai)

(3)

式中：Pi——单元接触应力的垂向分量；

Ai——单元面积；

Xi——形心坐标。

通过以上计算得到静态等效支点位置。

①两点支承等效支点位置Xd=0.378Lb；

②分布支承等效支点位置Xf=0.390 8Lb；

③接触方式的等效支点位置X=0.395Lb。

上述3种支承的等效支点位置均在船级社规定的(1/3～1/2)Lb范围内。

4.2 轴承支反力对比

4个轴承的单点支承的支反力可以从模型中直接提取，其余支承方式除后艉轴承外，其它3个轴承(弹性支点支承)支反力也可以直接提取，但后艉轴承的支反力须对所有接触节点的支承反力进行求和，结果见表2。

表2 支承反力比较

由表2可见，单点支承的轴承支反力与其它3种支承方式存在差别，而其它3种支承方式间相差较小。主要原因是单点支承将轴承刚度集中于一点，而其余3种方式支点多，不同程度地改变了轴承和整个轴系的刚度分布状况，从而引起轴承支反力的变化。

4.3 不同回旋速度下等效支点的变化规律

以艉轴转速为300、600、1 200 r/min为例，探讨不同回旋速度下后艉轴承等效支点变化的规律，见图4。

图4 不同支承方式与不同回旋转速的支点变化

图4表明，在不同支承方式下，支承点位置变化趋势基本一致。在低回旋速度(300 r/min)时，两点支承、分布支承及接触支承的等效支点位置接近正弦变化趋势。但随着回旋转速的提高，等效支点位置波动较大，如接触方式的等效支点位置相对静态时的0.395Lb，变化较大。

5 不同支承方式的模态分析

从运动学角度分析艉轴承刚度的分布对轴系回旋振动的影响。

假设后艉轴承刚度Kxx=2×108N/m不变情况下，不同支承方式的回旋振动模态固有频率见表3。

由表3可知，不同的支承方式对该轴系回旋振动的高阶固有频率影响较小。与二阶固有频率

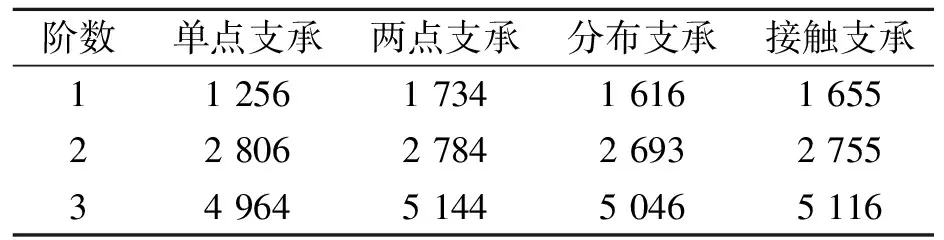
表3 不同支承方式的模态固有频率 1/min-1

对比，单点支承与其它支承的误差为0.8%～4.0%，三阶固有频率误差为1.7%～3.0%；对一阶频率影响较大，误差为28%～38%。这些与螺旋桨的重力悬臂作用有关。

表4为不同支承方式的轴系一阶各振动类型的固有频率。

表4 不同支承方式的一阶固有频率 1/min-1

由表4可见，应用等效支点计算的一阶各振动类型的固有频率均小于单点支承，误差为10%。

6 结论

1)3种支承的等效支点位置(两点支承Xd=0.378Lb，分布支承Xf=0.390 8Lb，接触支承X=0.395Lb)，均在船级社规定的(1/3～1/2)Lb范围内。

2)在低回旋速度时，两点支承、分布支承及接触支承的等效支点位置接近正弦变化，但随着回旋转速的提高，等效支点位置波动较大。

[1] 鲁 胜.艉轴承支承点位置对轴系回旋振动的影响研究[D].武汉：武汉理工大学，2012.

[2] 陈国钓，曾凡明.现在舰船轮机工程[M].长沙：国防科技大学出版社[M].2000.

[3] 周春良，刘占生，郑洪涛.轴承支承长度及间距对船舶轴系振动特性影响[J].船舶工程，2007，29(5)：16-18.

[4] American Bureau of Shipping.Marine Engineering Systems Department.Shaft alignment optimization software users manual & theoretical background[S].New York：American Bureau of Shipping，2006.

[5] 魏海军，王宏志.船舶轴系校中多支承问题的研究[J].船舶力学，2001(5)：49-54.

[6] MURAWAKI Lech.Shaft line whirling vibrations： effects of numerical assumptions on analysis results [J].Marine Technology，2005，42(2)：53-60.