一种斑马型压电俘能器的有限元分析

吴 昊，李开宇

(南京航空航天大学自动化学院，江苏南京 210016)

一种斑马型压电俘能器的有限元分析

吴 昊，李开宇

(南京航空航天大学自动化学院，江苏南京 210016)

提出了一种新型的俘能结构，其是利用压电效应并应用于微机电(MEMS)领域的设计。通常有效的能量捕获装置包括:悬臂梁类型的金属基层及与之粘结的较薄压电层，从而引起谐振响应。越短的悬臂梁其谐振频率越大，因此在微机电领域中，由于较小的结构使得悬臂梁难以形成共振。文中针对此问题提出了一种可以降低自身谐振频率的新型几何结构。对这种斑马型几何结构，利用Ansys仿真软件求解得出其在微机电领域内也可以接近发生共振。

微机电;悬臂梁;谐振频率;有限元分析

悬臂梁型能量捕获装置利用金属基片与压电层粘结，当装置的谐振频率与周围环境频率一致时可产生最大的输出电压，同时也使得压电材料的应力最大化。由于现有MEMS振动能量捕获装置的悬臂梁较短，使其谐振频率较大，这也是限制MEMS振动能量捕获装置发展的一个瓶颈。

近年来关于无线传感网络及以能量获取为主题的文献较多，关于文献的回顾在［1－3］。关注的是结构的机械性及如何降低其谐振频率到有效值。文献［4～5］较好的阐述了机电之间的耦合，在此不作赘述。Lu et al.［6］首先设计了 MEMS的捕能器，其梁的厚度是长度的1/10，但梁的谐振频率达3 kHz。梁的变形越大，得到的能量越多。因此，梁应尽量在谐振频率处。周围环境的频率一般在1～100 Hz之间，对于一个谐振频率达千赫级的结构来说，周围的环境都不足以使其振动。不恰当的厚度长度比导致了谐振频率较大的结果［7－8］，郑青龙使用了两个梁的结构，一个在顶端，另一个和其上下有一定距离，用以支撑质量块。这种结构既轻又坚韧，但谐振频率却达10 kHz。

Fang et al.是第一个试图利用较低厚度长度比(1/100)梁的人。其有效降低了谐振频率(600 Hz)文献［9～10］显示了此领域的发展趋势，得到的谐振频率有 460 Hz，100 Hz，971 Hz，180 Hz，256 Hz等。但在其些场合还不能达到要求，对换能器的总体设计的提高还是必需的。由于在MEMS内的空间限制，悬臂梁不可能太长。为此，有人提出了一种螺旋式的梁［11］，但是它的电极设置较复杂，实用性较低。为设计出低频的装置，提出了一种斑马型结构，如图1所示。文中优点是通过斑马型压电俘能器的设计，有效减小了应用于MEMS中压电结构的谐振频率，并通过有限元分析证明了其优势。

1 装置规格及斑马型结构的边界条件

1.1 斑马型结构的规格

如图1所示，这是两个平整的斑马型结构，分别由三根梁和十根梁组成，其尾端固定形成悬臂梁结构。支撑结构的平面被称为主平面。在主平面上结构可发生位移，并可由少量直梁及连接长方形块建立数学模型。每个梁的末端相连，且均可弯曲和扭曲。梁与梁的连接处较小，并以刚性连接作模型。每个梁的扭曲都会使下个梁的压电层有脱离主平面的趋势，相关的数学参数包括扭曲角度及刚臂长度。

图1 两种斑马型结构

表1 斑马型结构的规格

表1是斑马型结构的装置规格，每个梁的构造一样，均是有压电层和基层。基层可由硅氧化物制造，可以减少残留应力。在压电层，类似的弯曲可以产生电能。

1.2 斑马型结构的边界条件

整个斑马型结构有着悬臂梁的构造，即一端夹紧一端自由，对夹紧端的关键边界条件有梁的垂直变形，坡度和扭曲角度。

最后，扭曲角的条件方程为

式(1)可写为一个矩阵关系式

X轴向自由端可以为0或l，这取决于梁的数量。下面xend表示自由端的x向，在自由端的自然边界条件方程如下，力矩平衡条件方程为

切变应力平衡方程为 Qn(xend)=±mtip［∂2wn(xend，t)/∂t2］，其中 xend=0 对应正值，xend=l对应负值，可写为

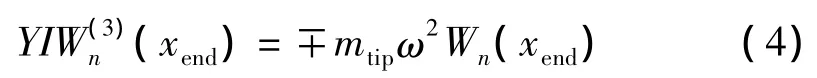
而扭曲平衡条件方程为

式(5)可写为一个矩阵方程

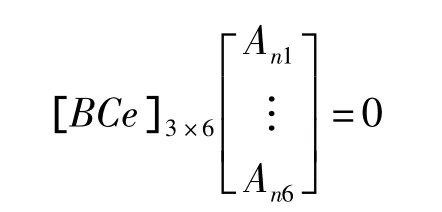
使用此结构除了可以减小谐振频率外，另一个优势是当梁的个数增加时，各自然频率的值变得接近了。对单根悬臂梁来说，其5阶频率值是一阶的70倍，而对于10根梁的结构则为10倍，这样就有助于增加能量获取的带宽。一般说来，在基本振形不是张力引起的情况下，增加质量块可以允许有更多的梁。相反，梁与梁的距离越大，可以有的梁数越少。

在扭曲振形中，梁都是平整的。每个梁的抬升高度与前一个梁都不同，主要是由前一个梁的扭曲造成的。在弯曲振形中，梁不再平整，会有些弯曲而连接处却很平整，这表明梁上的扭曲并不明显。对同样的结构，振形越高，扭曲振形和弯曲振形并存的情况便较明显。而振形对观察边界条件方程方面有较大价值。对所有振形可以确定的是，基于平面的位移W，及其导数，扭转角β在结构固定端的值均为0。而W，dW/dx，β在相邻两个梁尾端的值与其连接处的值相同。梁的弯曲度和弯曲处的坡度值均为0，这是评定是否为自然边界条件的重要前提。

2 斑马型压电结构的有限元分析

2.1 ANSYS有限元的模态分析

模态分析是用来确定结构振动特性的一种技术，振动特性包括自然频率、振形、振形参与系数，重要的是其为所有动力学分析提供了最基本的分析类型。使用模态分析有较多好处，如通过分析可以确定结构的谐振频率，然后根据特定应用场合避免或接近共振，也可以以特定频率进行振动;利用模态分析，可以认识到结构对不同类型的动力载荷是如何响应的;同时有助于在其他动力分析中估算求解控制参数。由于结构的振动特性决定结构对于各种动力载荷的响应情况，所以编程时在准备进行其他动力分析之前首先要进行模态分析。在Ansys中有几种常用的提取模态的方法，包括Block Lanczos法，子空间法，缩减法，PowerDynamics法，不对称法和阻尼法，使用何种模态提取方法主要取决于模型大小和具体的应用场合。

2.2 3种结构的仿真结果

图2为传统悬臂梁结构在模态分析下的振形及谐振频率等，如图2所示，其在0.1 N力载荷下的位移为1.056 cm，而谐振频率为255.522 Hz。

图3为三梁斑马型结构在模态分析下的振形及谐振频率等，由图3可见其在1 N力载荷下的位移为0.725 cm，而谐振频率为165.386 Hz。

在图4中，可以看到10梁斑马型结构的谐振频率是21.589 Hz，由以上仿真结果可以看出，当梁的数量增加相应的谐振频率值也会降低。但由斑马型结构的边界条件方程可知，当梁的数量超过10时，扭曲振形将替代弯曲振形成为第一振形，这将很难捕获到压电材料的最大能量。因为在能量捕获实例中，压电材料的上下层分布有电极。也就是说，能量的获取只在弯曲过程中而不是在扭曲过程中。这里关注的是振动产生的电压，因此应该关注第一弯曲振形中自然频率的改变，而不仅是谐振频率，若不是频率的特殊需要，应尽量使梁的个数＜10。

3 结束语

文中提出了一种新型的MEMS级几何结构，可有效降低了俘能装置的谐振频率，不需要为此增加梁的长度或尺寸，却能够使其与周围环境振动源形成共振。由有限元分析方法可以确定这种拥有低谐振频率微型俘能装置的可行性，这种斑马型结构的应用可以减少一阶弯曲自然频率，使之接近周围环境振动频率的范围。

文中所述分析过程均假定是E－B梁的弯曲与扭曲方式，并设定连接处是刚性的，把重量计入了模型的总体重量。有限元分析相对快速准确，也可用于以后的振动参数分析，参数研究有助于特性曲线的确定。文中的设计和一系列分析有助于设计低频的构件，用于基于MEMS的能量捕获装置，以适应绝大多数的野外环境。参考文献

［1］ANTON S，SODANO H.A review of power harvesting using piezoelectric materials ［J］.Smart Mater.Struct，2007，16(3):191－197.

［2］李邓化，居伟骏.新型压电复合换能器及其应用［M］.北京:科学出版社，2007.

［3］栾桂冬，张金铎，王仁乾.压电换能器和压电换能器阵［M］.北京:北京大学出版社，2005.

［4］ERTURK A，INMAN D.A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters［J］.ASME J.Vibr.Acoust，2008，130(4):41 －43.

［5］ERTURK A，INMAN D.Issues in mathematical modeling of piezoelectric energy harvesters ［J］.Smart Mater.Struct，2008，17(3):65 －81.

［6］LU F，LEE H，LIM S.Modeling and analysis of micro piezoelectric power generators for micro－electromechanical－systems applications［J］.Smart Mater.Struct，2004，13(1):57 －63.

［7］JEONY B，SOOD R，JEONG J H，et al.MEMS power generator with transverse mode thin film PZT［J］.Sens.Actuators，A，2005，122(1):16 －22.

［8］KUEHNE I，MARINKOVIC D，ECKSTEIN G，et al.A new approach for MEMS power generation based on a piezoelectric diaphragm ［J］.Sens.Actuators，A，2008，142(1):292－297.

［9］SHEN D，PARK J，AJITSARIA J，et al.The design，fabrication and evaluation of a MEMS PZT cantilever with an integrated si proof mass for vibration energy harvesting［J］.Journal of Micromech Microeng，2008，18(5):055017.

［10］LIU J Q，FANG H B，XU Z Y，et al.A MEMS － based piezoelectric power generator array for vibration energy harvesting［J］.Microelectron Journal，2008，39(5):802 －806.

［11］CHOI W，JEON Y，JEONG J，et al.Energy harvesting MEMS device based on thin film piezoelectric cantilevers［J］.Journal of Electroceram，2006，17(2 －4):543 －548.

Finite Element Analysis on Zigzag Transducers

WU Hao，LI Kaiyu
(College of Automation，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)

This paper addresses an issue in energy harvesting that has plagued the potential use of harvesting through the piezoelectric effect at the micro-electro-mechanical systems(MEMS)scale.Effective energy harvesting devices typically consist of a cantilever beam substrate coated with a thin layer of piezoceramic material to resonant at the dominant frequency of the ambient vibration.The fundamental natural frequency of a beam increases as its length decreases，so that at the MEMS scale resonance occurs orders of magnitude higher than ambient vibration frequencies，rendering the harvester ineffective.Here，we propose a new geometry for MEMS scale cantilever harvesters with low fundamental frequencies.To this zigzag configuration，we proved it can decrease its resonant to ambient by ANSYS.

MEMS;piezoceramic material;resonance;ansys

TM38

A

1007－7820(2012)08－043－03

2012-01-12

吴昊(1986—)，男，硕士。研究方向:数字信号处理，数字图像处理，无线传感网。李开宇(1969—)，男，博士。研究方向:数字信号处理，数字图像处理，无线传感网。