论振动体电动力学（Ⅳ）——共振场规范变换与对称性<br/>

论振动体电动力学（Ⅳ）——共振场规范变换与对称性

2012-01-16王鼎聪

石油化工高等学校学报 2012年1期

王鼎聪

（中国石油化工股份有限公司抚顺石油化工研究院，辽宁抚顺113001）

晶体可以自发结晶形成，表面光洁，线条笔直，美丽晶莹的外观，这是由晶体具有自范性所决定的［1］。由分子和原子组成的晶体具有高度的规整结构，这表明了分子、原子、甚至核子都具有严格的对称性，即平移不变性和转动不变性以及电荷守恒性［2］。

对称性在物理、化学和晶体中有着重要的应用。对称性分为两大类：一类是时空对称性，另一类是内部对称性［3］。数学做出了很大贡献，群论在数学层面上解释基本粒子的对称性，但是基本粒子对称性本质到底是什么？现在仍然是个迷。历届诺贝尔奖获得者，将物质的对称性与数学进行了关联，取得了很大的成就。1921年，Weyl引入了规范变换，将电磁场与理论定域标度变换下的不变性联系起来，但是这种设想没有成功。在量子力学建立后，Fock，Weyl和Pauli等发现了带电粒子与电磁场作用的量子力学是一种规范不变的理论。这种理论中运动方程在带电粒子波函数的定域位相变换保持不变。位相变换群是内部群，数学上是Abel群，即可交换群。1954年，杨振宁和Mills把规范不变的理论推广到内部对称的非Abel群，即不可交换群［4］。规范场论有两个困难，一是理论与物理现象的联系，二是规范场理论的量子化合重整化方面的问题［5］。后来提出了许多理论，量子色动力学等［6］，但是这些理论主要还是围绕数学来解决问题。物理对称性的本质还是没有得到很好解释。

晶体的宏观均匀性和对称性与原子、分子和质子的运动有何关系？原子的同一性和再生性与对称性有何联系？对称性究竟与物质结构有什么关系？本文以共振场［7］的观点来解释双共振－双进动－谐振［8］产生的基本粒子共振点［9］与对称性的关系。用粒子相互作用的共振场方式来解释基本粒子规范变换，晶体自范性，以及原子、分子、原子核及宏观物体与对称性的关系。

1 实验部分

1.1 实验药品

六水合硝酸镍（质量分数98%），分析纯；九水合硝酸铝，分析纯；尿素，分析纯；聚异丁烯马来酸三乙醇胺酯，自制；去离子水，自制；150HVI（润滑油基础油），工业品。

1.2 所用仪器

JEOL公司生产JEM2100型透射电镜，点分辨率0.23nm，用于观察纳米自组装体颗粒形貌和分散状况以及粒径大小及分布状况。

1.3 纳米粒子的制备

1.3.1 纳米氧化镍和纳米镍制备在搅拌条件下，将950g六水合硝酸镍与184g尿素加热至80℃，加入至同等温度条件下的12.5g聚异丁烯马来酸三乙醇胺酯和37.5g的150HVI油的混合物中，形成超增溶胶团。在120℃密闭反应3h，反应产物水洗3次，120℃干燥，550℃焙烧4h，得到纳米氧化镍［10］。在300℃微反应器中通入H2，纳米氧化镍被氢气还原得到了纳米镍。

1.3.2 纳米氧化铝－氧化镍混合制备在搅拌条件下，将452g九水合硝酸铝，267g六水合硝酸镍与324g尿素加热至80℃，加入至同等温度条件下的12.6g聚异丁烯马来酸三乙醇胺酯和53.8g的150HVI油的混合物中，形成超增溶胶团。在120℃密闭反应3h，反应产物水洗3次，120℃干燥，得到纳米氧化铝－氧化镍。

2 结果与讨论

2.1 共振点规范变换性

定义1：两个带电基本粒子在空间椭圆的相互运动，将产生周期性的电磁辐射相互作用的共振点，共振点具有规范变换性。

共振点的电量是最大值。只有在两个粒子绕各自质心进行圆周运动时，出现的最大电量位置，并具有电磁辐射的频率是倍数关系时才能发生共振效应。电量最大值，对外体现的就是电荷电量。

电子－质子共振点的规范变化的产生是来源于在共振点时，两个不同大小的椭圆运动，将会产生周期性的相对运动。其共振产生的电磁辐射是一指数函数，电子－质子两个粒子产生的电磁场符合内敛性原理的区间是在一很窄的区间内。对于电磁辐射两个指数函数，和，x1和x2是一正弦函数，两个函数的两个粒子只要辐射电磁场，指数函数总能找到一个频率成倍数的一个点，产生的共振效应点就是两个粒子的基本共振点。

当ex1是规范变换时，其产生共振作用的粒子电磁场与频率为倍数关系，即，

对于电磁辐射x1的，产生的场强Fuv在规范变化下不变，

电磁辐射x1相对应共振的电磁辐射x2应满足内敛性原理，是一个相反的场，这个场相应的场强v在规范变化下不变的，

定义2：产生共振点的两个电磁场都是规范变换的，共振点之间跃迁产生的电磁辐射也是规范变换的。

定义3 （共振点规范变换加和性）：任意共振点都是规范变换的，不同规范变换的共振点在一个圆周运动周期内的累加值仍然是规范变换的。

一个原子共振点反演是另一个相同原子的共振点，这两个反演的共振点可以产生内敛性的电磁场，能形成共振态。原子与原子的共振点在一个原子电子轨道运动周期中在任意位置都是唯一的，共振点绕核一周完成一次分子谐振周期。

由于电子在跃迁时，绕核的进动运动一周是分子光谱分子振动跃迁能级，或原子光谱的跃迁能级，即

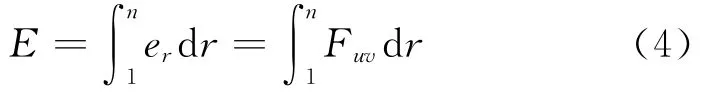
当n不同时，是uv不同的电磁场强F，为了防止混淆，这里用F代表电磁场场强，而E代表电子能量。以区别内敛性原理中电场E＋，E－。

在能量累加的E中，每个共振点电子与质子间的距离都是处于不同位置，两者的电势是不同的，电场不同，磁场也不同，如图1所示。E＋，E－不同，表示电磁场性质是不同的，根据规范理论，相同的电磁场是规范变换，而不同的电磁场是不规范变换的。

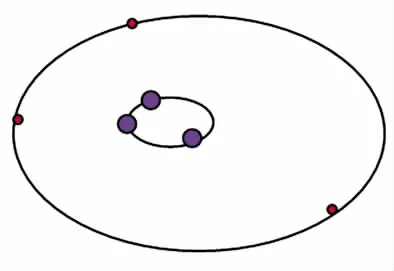
Fig.1 The specification of the resonance point transform schematic图1 不同共振点的规范变换示意图

尽管每个共振点的电磁场之间没有相同的规范变换，但是电子共振点绕核一周的积分，是将不同的规范变换累加成一个规范变换。这个性质表明，规范变换具有加和性。

2.2 共振点内敛性

泡利原理：在一个原子中不可能有两个或两个以上的电子具有完全相同的四个量子数（n，l，ml，ms）。分子轨道理论要求两个电子要采取自旋相反的↓，↑进入同一轨道。标准模型中，产生粒子相互作用的粒子都是费米子，自旋为1／2，并要求两个不同自旋进入同一轨道。

定义4 （共振点内敛性相互作用原理）：电子－质子，质子－质子，电子－电子的共振点相互作用的电磁场一定满足共振场内敛性相互作用原理。

共振场的内敛性原理，明确地提出，任何两个粒子相互作用，一定采取相反场发生作用，两个不同的场发生作用就相当两个不同的量子数。E＋相当于↑，E－相当于↓，↓，↑在共振场中可以表示电场方向相反。

共振相互作用是发生在共振点上，共振点是依据环境的温度和周边的其它粒子状态所决定的。无论处于何等环境，最后的共振点一定是相反场在起作用。

2.3 共振点的对称性—共振点点阵

对称性是客体在经过旋转，反映，反演和平移等操作后不可分辨的性质。共振点的对称性是来源于共振点的质子－质子，电子－质子共振方向不变性，这是一个规范变换，其共振场是具有规范变换性，具有对称性，是U1对称群的数学体现。

定义5：两个相同的粒子，辐射相同时，在内敛性作用下，粒子将保持相反场的共振进动作用，在共振点两个粒子形成共振稳定态的对称操作，满足U1对称群属性的共振点点阵。

如图2所示，在电子－质子的共振点时，电子与质子是具有固定的方向，这个方向性是原子、分子及晶体结构的产生的根本原因，这就是共振点点阵，具有反映、反演性质。

Fig.2 Symmetry lattice structure of the resonance point图2 共振点的对称性点阵结构

共振点点阵是一规范对称，源于电磁场的规范对称。随后产生了原子结构的对称性，分子结构的对称性，共振点的对称操作是分子和原子的对称性产生的根本原因。晶体结晶的点阵，结构基元与共振点的规范变换和对称性是直接相关的。如果承认分子谐振是源于电子与质子的进动，电子与质子之间运动就是固定的，有规律的，电子自旋－公转的耦合波产生的负电中心是时刻与质子自旋－公转的耦合波产生的正电中心形成共振，并保持最近的距离，这个最近距离就是共振点点阵。电子有顺磁性、抗磁性等磁性质，可以断定不同原子达到共振平衡态时，两个原子中共振作用的电子也是成对对称的，这是不同原子的共振点点阵产生共振相互作用的结果。质子－质子的对称性点阵结构，两个粒子产生的共振场符合内敛性原理，质子－电子也符合内敛性原理，也就是符合泡利不相容原理。

U1对称群能够对称操作的物体产生原因主要来源于基本粒子共振点点阵的对称性。物理中成对粒子的对称性，在共振场理论中，就是共振态共振点点阵的对称唯一性及共振点点阵相互作用的反映和反演性。质子的高速自旋和轨道的圆周运动产生的电磁场是具有共振性质的。质子共振点的进动产生点阵固定，表明质子在高速运动时，点阵结构是有规律的。质子之间的高速运动，产生的质子进动与核外的电子作用共同的进动产生了分子光谱，这从大量光谱数据可以得知，共振点点阵确实得到了光谱数据的支持。

2.4 纳米Ni晶体的对称性

图3是用分辨率为0.23nm进行的TEM分析。图3（a）是纳米氢氧化铝和纳米NiO的复合物。80nm直径的棒状体是纳米氢氧化铝，在上面分散着大量的5nm左右纳米NiO。图3（b）中箭头所指的是晶体产生晶格线，是纳米NiO产生的衍射峰。从晶格线来看，晶体是非常对称的结构，原子排列的非常整齐。这就需要原子中的电子是具有固定的取向，电子共振点的对称性是可以满足此要求的。

图3（c）中箭头所指的晶体更加具有自范性，已经形成非常规整的晶体，图3（d）中衍射可以证明此晶体是单晶，这就更加证明了这个晶体是具有非常对称结构，否则，晶体将会出现缺陷，不能形成单晶。高对称的结果是在电子衍射图中，显示一个对称的点阵结构。

Fig.3 TEM of Ni complexes图3 纳米Ni晶体的TEM

3 共振点角动量守恒

3.1 共振点角动量守恒运动

粒子都在自己的惯性轨道运动，轻子绕重子的圆周运动是轻子在等势能面内的惯性运动。

定义6：电子与质子共振点的点阵与质心是在一条直线上，电子的共振点与质子共振点都是在绕质心做圆周或椭圆运动。

质子－质子和电子－质子这两个点阵的相互运动产生了各自的电磁场，这两个电磁场在彼此上进行作用产生了共振点。

对于一个绕定点转动的物体而言，它的角动量等于质量乘以速度，再乘以该物体与定点的距离。可以进一步得出，为质量乘以每秒扇过的面积。

定义7：电子共振点与质子共振点的连线到质心，两个共振点的进动运动在单位时间内所扫过的面积相等。

角动量守恒，这个原理在原子中的电子绕核运动和地球绕太阳运动都是成立的。角动量守恒原理是物理学最基本原理之一。角动量守恒带来的是能量守恒，单位时间内所扫过的面积相等，就是能量守恒。

3.2 惯性圆周运动

牛顿第一定律将匀速直线运动和静止看成是惯性运动。惯性运动的主要特点是能量没有发生变化。那么除了匀速直线运动和静止外，做角动量守恒运动也是一种惯性运动。

定义8：质点在角动量守恒的圆周运动轨道上运动是惯性运动。

共振场是将质点在圆周上的角动量守恒运动、匀速直线运动和静止一样，都是惯性运动。依据就是两者之间能量是守恒的。

例如宇航员在空间站中犹如在地面上一样，空间站就是一个惯性体系，在空间站中水滴可以漂浮在空中，这一切性质都显示了惯性运动的性质。

高速绕核运动的电子和质子形成共振点的点阵后，也是一种惯性体系，这就是晶体能够稳定存在的原因，在一定温度环境下，晶体分子键长和方向都是固定不变的，都显示了电子与质子的惯性关系。

3.3 共振点角动量运动产生的原因

惯性离心力是小物体试图保持直线运动，而大物体对其有一吸引力，产生平衡时，小物体的运行轨迹是一圆周运动。惯性离心力和向心力的本质究竟是什么？牛顿万有引力和广义相对论是没有结论的。

共振场的方向：共振场方向是通量方向与旋度方向的矢量之和方向。共振场的电场与磁场是相等的，通量方向产生向心力与旋度方向产生离心力是相等的。

电子的电场分量与质子的电场分量的通量方向处于平衡态，方向相反，电子是被吸引的。电子的旋度分量方向与质子的旋度分量方向处于平衡态，方向相反，是电子的离心力方向。

由于共振场是电磁场，既有电场性质又有磁场性质，所以其通量不为零，表示A粒子谐振是处于某一时刻t1，电场是不为零的，设E为电场强度，H为磁场强度，同一电磁场的通量不为零：

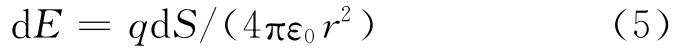
变化电场得到变化磁场，

任意时刻t1总有，

由于内敛型的电场E＋与内敛型的磁场HS能量是相等的。共振场方向是通量方向的电场力与旋度方向磁场力的合力，如图4所示。在弱共振场中，共振场的方向可以分解成电场通量方向的向心力，和磁场旋度方向的离心力，所以通量方向的向心力与旋度方向的离心力是相等的。这也解释了为什么绕核运动物体的向心力与离心力是相等的原因。惯性力在共振场中就是共振场力的一个分力，即沿磁场方向的力。

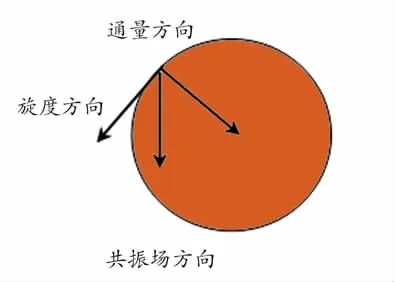
Fig.4 Resonance field direction图4 共振场的方向示意图

定义9：共振点角动量守恒运动是共振点电磁场中电场和磁场方向交替变换产生的运动。

共振点上电场是指向质心，而磁场方向指向水平切线方向。这样，共振点就受到了两个力，向心力和水平方向离心力的合力，这样电子就产生了角动量运动。

4 对称性共振点阵之间的电子跃迁几率

尽管电子本身不做波动性运动，但是电子辐射电磁波是具有波动性的，波函数概率可以解释电子跃迁的几率，而不是电子在某处出现的几率。共振的含义是指电子与质子产生的共振稳定态，将质子运动产生的电磁场能量定位零点能，对电子与质子的不同共振稳定态产生的电磁场进行量子力学处理。电子相对于质子共振场相互作用产生的共振点，其共振点在不同能量能级之间跃迁将满足波动方程。

定义10：粒子波函数的平方归一化是粒子基态和不同的共振激发态的能量几率总和。

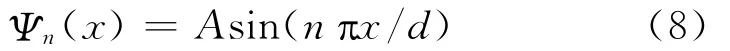
方程的系数A没有确定，利用归一化条件确定A。由于整个肼内空间，各种共振态出现的几率总体是1，所以波函数必须满足归一化条件：

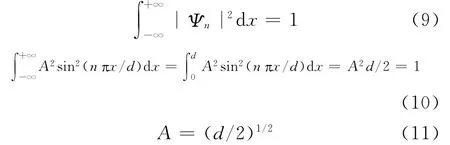
归一化波函数为：

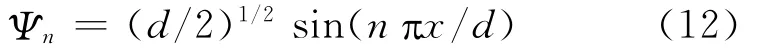
图5中左图是电子共振波长为3个驻波Ψn，电子与质子的不同共振稳定态电磁场。｜Ψn｜2是电磁场的平方，根据麦克斯韦的电动力学，电磁场平方是电磁场的能量密度。

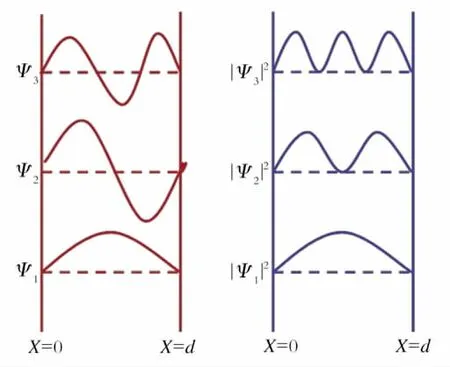
Fig.5 One－dimensional infinite resonance potential well of wave function and probability图5 一维无限共振势阱中波函数及几率

图5中右图是左图电磁场的相应能量密度所占的概率，也就是总能量的百分比，共振场对几率问题将有一个合理解释，就是一个电子共振激发态到另一个共振激发态产生的概率等价于量子力学的电子概率波几率。一个电子从一个激发态的共振点跃迁到另一个激发态的共振点将需要一定的能量，不同的激发态共振点之间需要的能量是不同的，并具有不同的比例，所有能级的能量之和是100%。

5 共振辐射规范变换与对称性

5.1 共振辐射电磁场的规范变换

共振场质心能量平衡原理提出了电子绕核心的运动处于电子与质子的共振态时，能量处于守恒状态时相互作用能与其相距质心的距离成反比。这个原理强调了粒子相互作用形成共振平衡态，粒子符合质心平衡，也就是满足牛顿多质点静力学平衡。

由于共振平衡态时，两个粒子辐射的电磁场是规范变换的，所以两个粒子也是规范变换的。两粒子相互作用辐射是规范变换，与质心分布有很大关系。当粒子从一个共振平衡态跃迁到另一个共振平衡态，如果粒子距离扰动很小，粒子吸收或放出的电磁辐射是规范变换的，这时粒子是在进行对称性变换。如果粒子从一个平衡态跃迁到另一个平衡态，质心平衡发生很大变化，如电子从中子中衰变放射出一个电子，这将会发生非规范电磁场变换，也就会形成非对称能级跃迁，这种情况出现在弱相互作用过程中。

定义11：电子绕核心的运动处于电子与质子的共振态时，能量处于守恒状态时相互作用能与其相距质心的距离成反比。质心平衡产生的电磁场是规范变换的。

规范变换共振辐射电磁场：电磁波的对称性表示，对称的电磁波是一正弦波，第i波的波形与任意第n波形完全相等。非对称性电磁波是任意时间的电磁辐射波形都不相等。设一相邻的单位时间dt所辐射的dλ1≠dλ2，也就是de1≠de2，这种电磁辐射没有特征的电磁波，即没有特征频率。电子的弱相互作用共振场产生的电磁辐射是非对称性电磁波。

当Δr≪r2，也就是电子的跃迁位置的移动几乎使r2没有变化。

质心平衡式：

式（13）可以看出电子由于没有位置的变化，势能不会发生变化，动能也可以在很短时间内从一个能级跃迁到另一个能级。ΔE／Δt产生的电磁场可以控制在时间趋近于零。此时产生的电磁辐射x1，相应的场强¯Fuv是可以保持电磁波的正弦性质，而电磁波是一个正弦性质就是一个规范变换电磁场。

5.2 共振场量子辐射的对称性

定义12：共振点点阵对称性的稳定平衡态共振态之间跃迁产生的电磁辐射，具有规范变换性，是对称性的电磁场。在满足质心平衡条件下，电磁辐射具有规范变换性。

粒子跃迁期间，A粒子辐射的电磁场，在相邻的单位时间dt所辐射的能量是相等的，dt1＝dt2，则

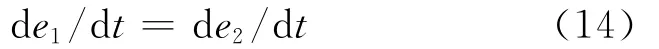
跃迁期间能量处于质心平衡态，由于质心是平衡的，电子跃迁没有发生位置移动，故共振点点阵是时刻可以保持对称形式，所以辐射是规范变换的。

5.3 共振辐射—光子

几百年来一直在争论光到底是波还是粒子。共振场将光子看成是一个能量包。这个能量包具有粒子性—直线性运动，是有无数的更微小的共振点的辐射能之和产生的。

定义13：光子是共振平衡态之间跃迁产生的规范变换的电磁辐射－玻色子，符合双共振－双进动谐振机理，是一个能量包粒子，具有直线性运动属性，波动性是共振点之和产生的能量叠加值显示的属性，是一宏观属性。

这个假设使波粒二象性产生了根本性变化，光子是粒子，而波动性是无数共振点之和产生的。

5.4 惯性力与共振辐射

共振辐射与电子－质子的共振有关，外层电子的任何跃迁实际上都可以关联到电子－质子的质心平衡运动，辐射携带着质心的信息。

任何物质的加速运动都是改变外层电子的电磁场规范变换，即电子的电磁场乘以一个外界施加的力或能量，这将使物质整体电子都要发生电磁场的规范变换，这就要求物质所有原子电磁场规范变换以惯性力形式体现出来。

5.5 共振辐射传播不需要以太

波动性学说，要求光传播必须有介质（以太）。以太的存在是光波动说所必须的。但是如果光的本质不是波动说所描述的那种水波传播方式，以太的存在就没有必要了。这就使光子传递不需要以太之类波的媒介。由于对光的本质认识的不同，将会使相对论的许多根基产生了动摇。

共振场的光是两个共振体之间的共振平衡态产生了跃迁，两个平衡态之间能量差，就是以光辐射形式与外界交换，光辐射是玻色子，没有质量，是以一个周期波包形式向前方直线传播，其波动性就是这个波包的电场磁场交替变化的结果。

6 共振辐射电磁场对称性破缺

6.1 质心平衡的对称性破缺

弱相互作用是什么引起的？用共振场观点，就是粒子在跃迁的过程辐射的能量是非对称的电磁波。电子在以能量加速度的加速过程就是能量非对称的结构。

定义14：两个粒子处于对称性时，m1r1＝m2r2，破缺时，则m1r1≠m2r2。质心平衡差很大的体系是对称性破缺的。任意相同时间dt1＝dt2辐射的de1≠de2，即dλ1≠dλ2，这种电磁波是非规范变换的，对称性破缺的。非对称电磁辐射不能与任何对称性电磁场发生相互作用。

当质心平衡是超级不平衡时，则粒子跃迁期间，能量对称性是破缺的，其微分值都是对称性破缺的。A粒子辐射的电磁场，在相邻的单位时间dt所辐射的能量是不等的，若dt1＝dt2，则

这种电磁辐射没有特征的电磁波，即没有特征频率，是非规范变换的电磁波，这种电磁波就是著名的中微子，是对称性破缺的。

从群论的对称性规则可知，尽管在跃迁区间，辐射能量的微分是非对称性的，但是总的辐射之和电磁波的正弦函数是对称性的，这是由于A粒子从一个对称性的共振平衡态到另一个对称性平衡态之间辐射的能量总和也是对称性的，这是对称性的基本性质所决定的。

而非对称性电磁场是非正弦电磁波，没有规范变换性，是不能被电磁仪器接收的，这种信号不能引起共振效应，而特拉斯发明的电磁交变设备基本都是利用谐振原理发射和吸收信号，即交流电和电磁波都是电磁场的谐振波。

电子辐射出非对称电磁辐射，使能量不守恒。辐射的能量如何使其守恒？可大胆假设非对称电磁辐射守恒方式。

由于电子从中子中跳跃到原子的电子轨道，能量逐渐辐射的结果是任意相邻相同时间间隔的电磁辐射φ在不断的调整其频率与所要去的共振态的频率相等或成倍数，辐射场的频率在逐渐降低，最终达到共振频率：

由于电子相邻无穷小的能量不等，导致任意相邻的能量没有正弦电磁场的对称波形的特性，没有固定的波长，也就是c＝λν中的λ值一直是增加，即：

原子的半径分布在0.053～0.270nm，电子半径约2.8fm，从核内衰变的中子向核外轨道跃迁需要跨越自己半径105～106倍的距离，这是非常遥远的距离，一般衰变的半衰期长达50～60s。除了距离的遥远，这种跃迁还受到电子与质子的质心平衡控制，在达到质心平衡点时，就需要长时间才能到达原子中电子－质子平衡共振态的电子轨道。由于在此期间，电子为了寻找平衡态的位置，其能量一直是降低的，并辐射出任意相邻的φ1和φ2都没有相同特征的非对称性电磁场辐射，来使电子本身的能量达到守恒状态。

这种没有固定波长，波长逐渐增大的非对称电磁能量辐射，是非对称电磁辐射，任意的de1≠de2。这种任意相邻能量不等，也就是宇称都是不守恒的。

由于没有一定的频率，没有固定的能量范围，所以这种非对称电磁辐射，就形成了粒子四大基本力之一的非常神秘的弱相互作用力。

弱相互作用力几乎不与任何物质发生作用，是与其电磁辐射的非对称性有直接关系。这种非对称性的电磁辐射，不能与具有对称性的电磁波发生共振效应。这种对称性破缺的电磁波是没有任何特征频率的非对称电磁波，不可共振的电磁辐射是不会被任何具有对称性电磁波仪器所能探测到的，同时也不会被具有对称性电磁场的所有分子、所有的原子和所有的化合物共振吸收，也就是说，人们所感知的世界都是具有对称性电磁波的，非对称性电磁波是无法被感知。

6.2 非对称性共振辐射——中微子的归宿

定义15：非对称电磁波流入真空中，各种非对称辐射的叠加形成了真空的背景温度场。非对称的温度场可以使费米子凝聚态中的电子发生跃迁，吸收的非对称辐射能转化成原子共振场对称性共振能。

微波背景辐射表面真空中的基础温度场是－3.5K，是各向同性的。按照共振弱相互作用跃迁时，必能辐射非对称性的电磁波，这种非对称电磁波是不能与任何对称性的电磁波进行共振，也就是不能与任何强相互作用粒子进行作用。这个能量将流入真空中，形成了宇宙的背景辐射。按照牛顿的设想，宇宙是无穷无尽的，各个方向辐射的非对称性电磁波应该是相等的。

弱相互作用辐射的非对称电磁波生成的背景辐射，形成了温度场，当有一些处于费米子凝聚态的原子需要温度场能量时，这个能量又转化成对称性的电磁辐射。光速变化的电磁场产生的能量加速度，受到质心平衡和角动量守恒的限制，长距离长时间才能到达平衡态时所产生的加速度定义为弱共振场加速度。考虑距离的因素，在长距离到达共振平衡点过程中，能量将缓慢释放，需要很长的时间，能量变化的加速度很小，这是一个弱加速度，如图6所示。

7 粒子相互作用的共振模型

7.1 原子和分子的共振模型

电子绕核运动过程共振点是受分子、晶体中相邻原子的影响，共振点不断调整，使其符合当时的热力学环境。共振点调整到适宜温度条件，电子发生能级跃迁，在这个能级中某个方向共振点的点阵是能量最低。

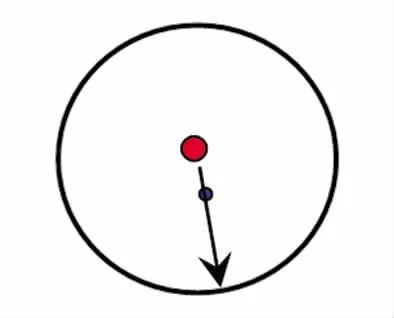
Fig.6 Weakly interacting particle transition图6 弱相互作用粒子跃迁

原子核中的质子呈现点阵结构，与之相对应的电子在原子核外原子轨道也相应的形成了点阵结构。

电子与质子的进动，形成了有规律的电子进动运动，核外的电子与质子一样都呈现出类似于晶体结构的排列方式。电子的对称性，既符合泡利不相容原理，又符合电子进动产生的对称性排列，形成了电子成对性。晶体的对称面电子排列恰好符合磁性质形成了反相，磁显示为中性特点。电子2，8，18的晶体排列方式，都会使磁性质符合物理实在。

按照分子轨道理论解释就是，两个不同自旋的电子进入了相同的轨道，形成的电子云可以相互作用形成分子成键轨道。按照共振场理论解释化学键强烈互相吸引的本质，就是两个电子产生的共振点发生内敛性共振相互作用。

7.2 原子核的共振模型

电子规整性、对称性和电子的进动性，表明质子具有成对的对称性，质子在核内的对称排列最好的方式是原子核具有晶体性排列。原子核具有晶体性排列是一个质子－质子高速绕核心运动总的效果。若质子绕核心运动是进动的，那么原子核形状是椭圆形的，质子－质子绕核心的高速进动，质子与质子形成了对称结构。

质子1绕核运动产生了共振点电磁场φ1，质子2在原子核中是质子1的镜像，绕核运动产生了共振点电磁场φ2。因为质子1与质子2的质量相等，两者共振点的绕核运动是绝对对称的，呈镜像的结构，外层的电子同时也与相应质子做共振进动运动，这样就形成了核内核外都是对称性的镜像结构，如图7所示。两质子的同向运动可以产生相反的电磁场，相反场可以形成具有反演的内敛性共振场，并形成两个质子绕核进动运动。

定义16：原子核呈能量壳层结构分布，每个壳层内核子之间都是共振稳定态。核子从一个共振稳定态跃迁到另一个共振稳定态，并辐射或吸收量子能量。每层核子分布呈晶体结构分布，并呈两两对称分布，每对质子互成反演对称的共振态。

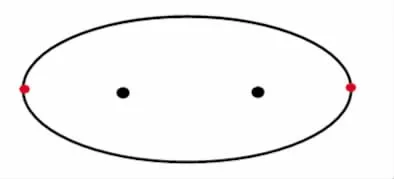
Fig.7 The electron and proton the symmetry precession movement图7 电子与质子对称进动运动

根据以上的假设，可以解释不同元素原子的形成。由于质子和中子是两种不同能量、不同电荷的核子，所以两者之间的共振不是最强的共振态，而相同的质子或中子之间的共振能达到最大能量的共振态。当每一壳层的质子或中子各自填充满相应的晶体结构后，将开始下一能级的填充。按此原理可以做到每一能级的中子和质子互不影响，这样可以利用每一壳层能级填充最多的核子，使核子达到最大的填充密度。

提出相应原子核的共振模型：

（1）核力是核子之间共振作用产生的，核子通过共振可以达到共振相应频率所具有的共振结合能；

（2）核子间共振满足共振隧道效应的共振辐射交集φ1∩φ2→1的强相互作用；

（3）原子核是有层次的，层的能级处于分立的量子态，核能级中各个质子的共振点呈现为晶体壳层结构中的点阵。

（4）每一壳层有质子和中子共振点，分为两个分层，质子共振点在内层形成晶体多面体结构，中子共振点在外层形成晶体多面体结构。在外层完整对称结构的中子稳定共振态起到了平衡质子、完成分立能级的作用，稳定共振态是晶体的高对称结构。

在核结构假设中，最重要的是将质子的运动共振点看成了晶体中的点阵结构，共振点呈点阵结构，由原子核的各个质子形成点阵将会组成晶体结构。

8 玻色子与费米子相互作用

8.1 光子在介质中的折射－强相互作用

光子在溶液中会发生折射作用，这是光子这个能量包与原子中电子－质子的共振场发生了强相互作用，使其运行路线发生了改变，所以光子折射这种使光子直线性运行发生改变，一定是光子已经发生了强相互作用。

8.2 光子在宇宙中能量衰减－弱相互作用

任何两个费米子（或费米子聚集体，即宏观物体）相互作用是靠玻色子传递能量。任何两个粒子都是采取相反场作用。由于宏观物体的距离一般都远远大于其原子半径和分子半径，所以宏观物体都是采取两个粒子辐射的交集趋于零方式进行，这个趋于零的交集，采取了万有引力方式作用，这就是最小的物体（费米子或费米子聚集体）共振相互作用。

由于只有辐射相同频率的粒子才会产生强相互共振作用，所以对于费米子两个粒子辐射的交集趋于零是万有引力。对无质量的玻色子，费米子或费米子聚集体与玻色子的作用将会更小。由于玻色子无质量，两者发生共振作用玻色子没有接受能力，即两个玻色子不会发生相互作用。但是根据共振场的内敛性假设，任何两个相互作用的场都会发生内敛性作用，那么对于光子这个没有质量的玻色子将会存在一个最小的作用，假设这个作用方式是以光子能量衰减方式体现，这个光子最小的衰减程度就是光子与宇宙中所有物体的相互作用衰减常数即哈勃红移常数。共振隧道效应因子P＝1时，表明两个质点没有强相互作用，即φ1∩φ2＝0，没有相同的共振频率，隧道是贯穿的。在这两种相互作用下，宇宙处于两种类型反应：核反应，分子化合分解、原子结合等强相互作用，这些反应导致了宇宙大的变化，超新星等现象，甚至局部大爆炸现象发生。另一类是星体间自然的热力学平衡运动，这是质心平衡运动，形成一个无边无际的巨大热力学平衡体系。相互之间靠光辐射传递能量，使之保持能量平衡状态，保持质心平衡运动状态。

共振隧道效应这个性质，将直接导致任何物体都会有相互作用最低值。同样，在宇宙中到处游荡的光子也不例外，光子也与具有质量的任何物体都会发生最弱的相互作用，将其定义为光子的共振衰变，衰变常数就是哈勃常数。

定义17：单一辐射光的强电磁共振场的辐射波与势垒为零的弱共振场中产生共振相互作用。高能量状态的单一辐射光能量衰减，导致频率红移，红移的规律符合哈勃定律，其光衰减常数与哈勃常数等价。

在宇宙学研究中，哈勃定律成为宇宙膨胀理论的基础。但哈勃定律中的速度和距离均是间接观测得到的量。速度—距离关系和速度—视星等关系，是建立在观测红移—视星等关系观测数据和一些理论假设上。哈勃常数H0定为77km s－1·Mpc－1是大量观测的结果。既然哈勃定律是一个观察的物理事实，其光的红移值是确定的，这是实验事实。

从量子力学得知万有引力与电磁力的比例系数为10－40，从这个系数的巨大差别也可以看出，弱共振场（产生万有引力）相互作用极弱，对称性强共振场（产电磁力）的势垒很高，隧道几率非常低。

单一辐射光的强共振场的电磁辐射波具有势垒。根据共振场势垒假设，势垒再高也具有一定的隧道效应，势阱内的电磁波有一定几率与势阱外相互作用。势垒为零的弱共振场可以与任何物质进行作用，与强共振场势阱内的电磁波也可以有一定相互作用的几率。尽管弱共振场与单一频率电磁辐射相互作用极其微小，毕竟它们之间是可以产生作用的，这就会使在宇宙中传播的光与各种星体产生作用，使光的能量不断降低。根据宇宙观测数据，这里规定弱共振场与单一辐射光的强共振场的电磁辐射波相互作用常数与哈勃常数H0一致。