一种基于二进制编码的最小生成树算法

王防修

(武汉工业学院数学与计算机学院，湖北武汉430023)

许多应用问题都是一个求带权无向连通图［1］的最小生成树［2］问题。例如：要在n个城市之间铺设光缆，主要目标是使这n个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同;另一个目标是使铺设光缆的总费用最低。这就需要找到带权的最小生成树。

在求带权无向连通图的最小生成树时，最经典的算法就是Prim算法和Kruskal算法［3］。这两个算法都是通过求解局部最优达到求解全局最优，即我们通常所说的贪心算法。一般来讲，局部最优解往往不是整体最优解，而是近似最优解。由于最小生成树的特殊性，用贪心算法［4］能够准确地计算出它的全局最优解。然而，无论Prim算法还是Kruskal算法，都只能找到带权无向连通图的一个最小生成树。如果一个带权无向连通图有多个最小生成树，要想找出所有的最小生成树，用 Prim算法或Kruskal算法都是无能为力的。至于所谓用遗传算法求最小生成树，由于该算法是一种近似算法，可能连一个最小生成树都找不到，最好的情形也是只能找到一个最小生成树。因此，能否找到一种在全局范围内寻找所有最小生成树的算法?到目前为止，还没有相关文献作这方面的工作。本文试图用二进制编码的方式来解决这个问题。

1 理论基础

定义1用深度优先法或广度优先法遍历一个无向图，如果所有顶点都能被访问到，则称该图是连通图;否则，称该图是不连通图。

定义2设一个带权无向连通图［5］有n个顶点和m条边，如果删除m-n+1条边后，该剩余图仍然是连通的，则称该剩余图为生成树。

定义3在一个带权无向连通图的所有生成树中，所有边的权值之和最小的生成树是最小生成树。

性质1如果一个带权无向连通图有n个顶点，那么它的生成树只有n-1条边。

证明：如果它有n条边，那么它一定有回路，因此它就不是生成树。另一方面，如果它只有n-2条边，那么这n-2条边最多只能连接n-1个顶点，还有一个顶点没有被连接。

定义4对于一个无向图，如果用字符‘1’表示图中的两个顶点之间存在边，用字符‘0’表示两个顶点间不存在边，则我们称这种用二进制字符串表示的图为对图的二进制编码。

定义5设一个无向连通图有m条边，如果我们用长度为m的二进制字符串表示它的生成树，则称该二进制字符串是对应该生成树的染色体，其中染色体的每一位对应无向图的一条边。

性质2设G是一个含有n个顶点m条边的无向连通图，如果用染色体表示该无向图的生成树，则染色体是长度为m的含有n-m+1个‘1’字符和2m-n-1个‘0’字符的字符串。

定义6如果一个染色体对应带权无向连通图的最小生成树，则称该染色体是最优染色体。

性质3如果找打一个带权无向连通图的最优染色体，则它所对应的最小生成树确定。

2 算法设计

2.1 带权无向连通图的矩阵表示法

设G是一个含有n个顶点m条边的带权无向连通图，则可以用一个n×n阶矩阵表示：

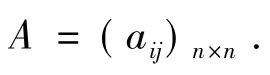
其中

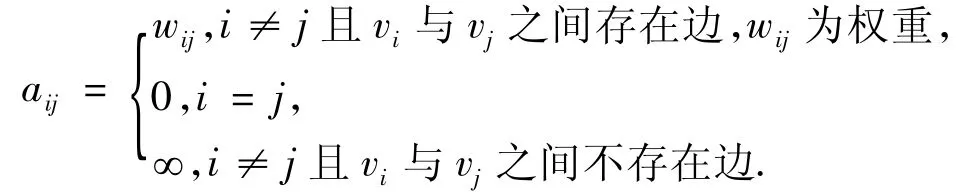
2.2 连通的判断

算法的中心思想就是从带权无向连通图的生成树中找出最小生成树。虽然生成树是从图的m条边中去掉m-n+1条边形成的，但仅仅删除m-n+1边还是不够的，还必须保证删除的剩余图还是连通的，否则就不是生成树。

可以通过使用深度优先法或广度优先法对剩余图进行遍历，如果图的所有结点经过一次遍历都可以搜索到，则该剩余图就是生成树。否则，剩余图一定不是生成树。

因此，通过深度优先法或广度优先法对剩余图进行遍历，可以将带权无向连通图的所有生成树找出来。然后，从生成树集中找出最小生成树就比较自然了。

2.3 对生成树进行二进制编码

由于带权无向连通图有m条边，因此需要用长度为m的二进制字符串即染色体表示该图。当染色体的每一位都是字符‘1’时，该染色体就是表示该带权无向连通图。一方面，带权无向连通图的生成树只有n-1条边，故它所对应的染色体只有n-1个字符‘1’和m-n+1个字符‘0’;另一方面，由n-1个字符‘1’和m-n+1个字符‘0’组成的染色体不一定对应一棵生成树，故需要判断该染色体所对应的剩余图是否连通。

因此，判断一根染色体是否对应一棵生成树，执行步骤：(1)从“00…011…1”(该染色体由左边的m-n+1个‘0’字符和右边的n-1个‘1’字符组成)到“11…100…0”(该染色体由左边的n-1个‘1’字符和右边的m-n+1个‘0’字符组成)的染色体中筛选出只含有n-1个字符‘1’的染色体;(2)从(1)筛选出的染色体中进一步筛选出生成树连通的染色体。

3 算法描述

设G是一个含有n个顶点m条边的带权无向连通图，则生成图G的算法过程如下。

Step1：初始化i=2n-1-1，最优值shortpath=-1，长度为m的二进制字符串 str=“00…0”(m个‘0’字符组成)，以及建立染色体每一位与带权无向连通图的某一边的对应关系。

Step2：将i转化为长度为m的二进制字符串，具体转换过程如下。

(1)执行语句 itoa(i，str1，2)，可以将整数 i转换为二进制字符串。

(2)求出二进制字符串str1的长度，只需执行l=strlen(str1)。

(3)执行 strcpy(str+m-l，str1)，就可以得到 i所对应的染色体str。

Step3：统计染色体str中所含字符‘1’的个数c。如果c≠n-1，则转向step6。

Step4：判断染色体str所对应的图是否连通。如果不连通，则转向step6。

Step5：求 str所对应的生成树的边权之和curpath。如果 curpath＜shortpath，则执行 shortpath=curpath，同时保存该染色体;否则，只保存该染色体。

Step6：执行 i=i+1。

Step7：如果 i≤2m-2m-n+1+1 ，则返回 Step2。

Step8：从保存的生成树染色体中将边权之和等于shortpath的染色体(最优染色体)选择出来。

Step9：输出所有最优染色体所对应的最优生成树。

4 算法测试及比较

4.1 算法实例

例已知如图1所示的带权无向连通图G，求G的最小生成树。

图1 带权无向连通图G

解：由于带权无向连通图G的定点数n=5和边数m=8，因此程序执行算法的过程如下。

Step1：i = 15，shortpath = -1，str=“00000000”，染色体的8个二进制位从左到右依次与边 (v1，v2) 、(v1，v3) 、(v1，v4) 、(v2，v3) 、(v2，v5) 、(v3，v4) 、(v3，v5) 、(v4，v5) 相对应。

Step2：执行语句：itoa(i，str1，2);l=strlen(str1);strcpy(str+m-l，str1);得到i所对应的染色体str。

Step3：如果str所含字符‘1’的个数不等于4，则转向step6。

Step4：如果染色体str所对应的图不连通，则转向step6。

Step5：求str所对应的生成树的4条边的权值之和curpath。如果curpath＜shortpath，则用curpath替换shortpath，同时保存染色体str;否则只保存染色体。

Step6：执行 i=i+1。

Step7：如果 i≤241 ，则返回 Step2。

Step8：从保存的生成树染色体中将4条边权值之和等于 shortpath=14的染色体“01101001”和“11100001”选择出来。

Step9：染色体“01101001”和“11100001”所对应的最优生成树分别如图2，图3所示。

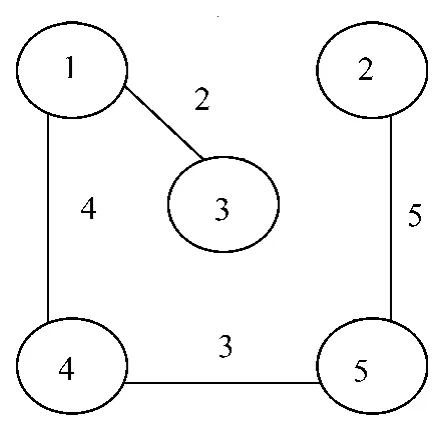
图2 01101001所对应的最小生成树

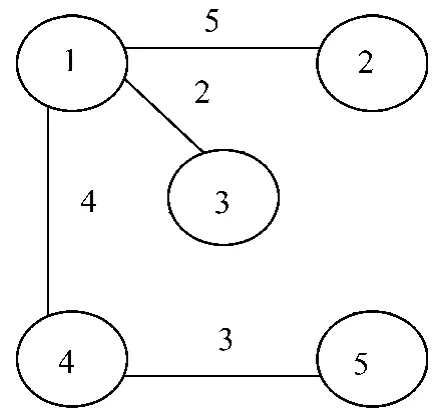
图3 11100001所对应的最小生成树

4.2 算法比较

如果分别用Prim算法和Kruskal算法求解图1的最小生成树，都只能得到如图2所示的一棵最小生成树。因此，当一个带权无向连通图的最小生成树不止一个时，Prim算法和Kruskal算法都无法求出所有的最小生成树，它们永远只能求出其中的一个最优解。

本算法先利用染色体表示各种不同的生成树，然后从所有这些生成树中找出所有最小生成树。因此，本算法通过巧妙地利用二进制编码来达到全局寻优的目的。

Prim算法和Kruskal算法本质上都是通过局部最优达到全局最优，因此寻优的速度快。本算法由于是全局寻优，故寻优的速度比较慢，但它可以找到所有的最优解。

5 结束语

针对Prim算法和Kruskal算法都不能寻找一个带权无向图所有最小生成树的缺点，本文提出了一种从全局范围内寻找一个带权无向图所有最小生成树的二进制编码算法。该算法充分利用深度优先遍历算法和最小生成树的性质，将不满足生成树的染色体淘汰，从而极大地提高了全局范围内的寻优速度。实验表明该算法能够实现全局寻优和找出全部最小生成树，并使寻优效率在整体上得到改善。

［1］ Fred Bucldey，MaryLewinter.图 论 简 明 教 程［M］.北京：清华大学出版社，2005.

［2］ CormenTH，Lleiserxon CE，RivestRL.Introducton to Algorithms［M］.USA：MIT Press，2001.

［3］ 高一凡.《数据结构》算法实现及解析［M］.西安：西安电子科技大学出版社，2002.

［4］ 候识忠.数据结构算法程序集［M］.北京：中国水利水电出版社，2005.

［5］ 刘瓒武.应用图论［M］.长沙：国防科技大学出版社，2006.