免赔额与停止损失保费探研

魏艳华,王丙参,徐长伟

(1.天水师范学院 数学与统计学院,甘肃 天水 741001;2.中原工学院 理学院,河南 郑州 450007)

免赔额是指由保险人和被保险人事先约定，被保险人自行承担损失的一定比例、金额，损失额在规定数额之内，保险人不负责赔偿.免赔额是被保险人自己承担的损失额度，因此免赔额能消除许多小额索赔，损失理赔费用就大为减少，从而可以降低保费，于是免赔额条款在财产、健康和汽车保险中得到广泛使用.再保险是指保险人在原保险合同的基础上，通过签订分保合同，将其承担的部分风险向其他保险人进行分保的行为．对于停止损失再保险，当自留额的均值固定时其自留风险的方差最小，还可以得到更强的结论：任何厌恶风险的决策者都偏好停止损失再保险所对应的自留风险[1-5]．可见对免赔策略及停止损失再保险的研究是非常必要的，鉴于此，本文研究了免赔策略与截断分布之间的关系，并用截断分布刻画停止损失再保险，对停止损失保费的计算做了初步探讨．

1 截断分布与免赔

对于满足P(X>d)>0的给定值d，超损变量(每次赔付r,v)Y≜X-d，若X>d,平均超损函数eX(d)≜EY=E(X-d|X>d)，Y也称为左截断平移变量[5]，左截断是因为d以下的观测都丢弃了，平移是因为指所有的观测量都减去了d，显然其中S(x)=1-F(x)称为生存函数.左删失平移变量(每次损失r.v)Y≜因为没将小于d的值忽略而是定义为0，所以称为左删失，

2 停止损失保费的计算

令k=1可得

设X～N(μ,σ2)，U～N(0,1)，则X=σU+μ，于是E[(X-d)+]=E[σU+μ-d)]=

E[(X-d)+]．

设S～Γ(α,β)，

[(S-d)-(S-d)+][(S-d)+]≡0，

(S-d)k={[(S-d)-(S-d)+]+(S-d)+}k=

利用恒等式对[S-(S-d)+-d]k展开，可以计算出自留损失S-(S-d)+的矩．

设X～LN(μ,σ)2，则X=eY，其中Y～N(μ,σ2)，则

E[(X-d)+]=E[(eσU+μ-d)+]=

如果P(U≥0)=1，EU=μ，则

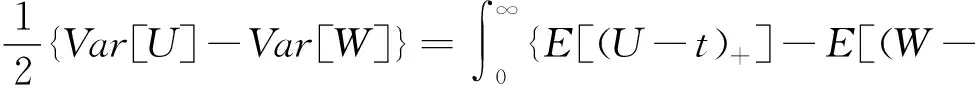
定理1 如果对某固定h>0有P(S=kh)=fk≥0,k=0,1…，对其他所有x有P(S=x)=0，即S是格点的，则给定d=jh，j为非负整数，则有

证明

E[(S-d)+]=∑x>d(x-d)f(x)=

特别有:令d=(j+1)h，则有

E[(S-jh)+]-h[1-F(jh)].

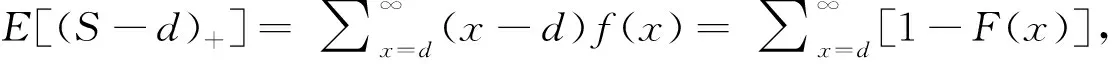
证明由于F(x)=F(a)，所以当a≤x≤b时，

E[(S-a)+]-(d-a)[1-F(a)].

令d=b可得

代入上式可得结论成立.

参考文献：

[1]王丙参,魏艳华,冉延平.停止损失再保险[J]齐齐哈尔大学学报,2009,25(2):76-77.

[2]魏艳华,王丙参,宋立新.合作保险与最佳竞争力[J].重庆文理学院学报,2010,29(2):1-3.

[3]魏艳华,王丙参,徐长伟.停止损失保费的计算与近似[J].天水师范学院学报,2010,30(5):18-20.

[4]纪玉卿,曹玉松.最优成熟再保险决策模型研究[J].数 学的实践与认识,2008.38(15):98-101.

[5]Klugman S A ,Panjer H H.损失模型从数据到决策[M].吴岚,译.北京:人民邮电出版社,2009.

[6]R.卡尔斯.现代精算风险理论[M].唐启鹤,胡太忠,成世学,译.北京:科学出版社,2005.