长距离线路工程投影变形值控制方法分析

李沛鸿，王富麒，刘陶胜

（江西理工大学建筑与测绘工程学院，江西赣州341000）

长距离线路工程投影变形值控制方法分析

李沛鸿，王富麒，刘陶胜

（江西理工大学建筑与测绘工程学院，江西赣州341000）

根据投影变形理论，离坐标原点越远，等距离变形值越大，在长线路工程中，需要充分考虑如何正确选择坐标系统，减少投影变形，提高控制网解算精度.针对某高速公路，介绍了长度投影变形理论，分析线路工程长度变形量与坐标系选择的关系,然后计算出在各种坐标系统下的投影变形值，并对计算结果分析比较，最后提出建立带抵偿高程面的任意带高斯投影坐标系是消除或减少控制网的长度变形更有效的方法.

投影长度变形；坐标系统；抵偿投影

在公路建设中，根据《公路勘测规范》（JTG C10-2007）要求，测区内投影长度变形值不得超过2.5 cm／km.因此，在进行长距离线路工程测量控制网的设计时，应首先分析控制网边缘地区变形量的大小[1-2]，以确定其是否满足规范的要求.而如何依据规范要求，结合工程实际情况，建立合理的控制测量坐标系，是长距离线路工程测量中首要解决的难题.为了满足控制网边长变形精度要求的需要，可通过设计投影面和中央子午线，构建新的坐标系统，达到较大抵偿控制网变形的要求.因此，文中先对投影变形理论进行分析，再结合某高速公路建设项目，讨论了线路工程测量中如何合理选择投影面与投影带，为类似工程提供了一定的参考价值.

1 投影变形与控制

1.1 投影变形理论

控制网观测成果进行平差前需要进行两次投影归化，即先将实测长度归算到参考椭球，再将归算后的成果归算至高斯平面，在两个归算过程中，都存在投影变形，计算过程如下：

（1）地面水平边长归算到归化面（参考椭球面）上的投影变形：

（2）参考椭球面边长投影至高斯投影面有变形：

长度投影变形等于两次投影变形之和：

式（1）至式（3）中，ΔS1：地面基线归算至参考椭球面引起的归算边改正数；S：实地水平边长；Hm：归算边高出归化面的平均高程；R：归算边方向参考椭球弧法截弧的曲率半径；ΔS2：由椭球平面上归算至高斯平面上的距离改正数；S0：投影到椭球平面上的长度；ym：基线边两端点横坐标平均值；Rm：椭球面平均曲率半径.

由上可知，Hm值是跟投影面高程有关，ym值跟测区选用的中央子午线有关，在长距离线路工程中，线路两端跨度较大，端点处横坐标值会比较大[3].当控制网与各边已经确定，综合变形量的大小跟Hm和ym有关.

1.2 控制变形的基本方法

为了控制边长变形量，归算测量结果的参考面的选取有以下3种方法：

（1）要选合适的高程作为参考面，须改变Hm，以抵偿分带投影变形，即抵偿投影面的高斯正形投影.抵偿高程投影面的选择[4－5]：

以国家3°带投影坐标系为例，当测区位于中央子午线一侧时，

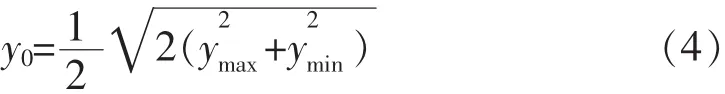
当测区跨越中央子午线时，

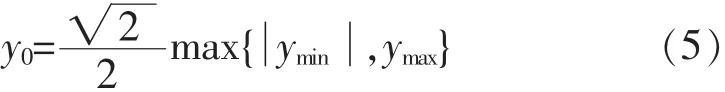
（2）改变ym，适当移动中央子午线，来抵偿由高程面的边长归算到椭球平面上的投影变形，即任意带高斯正形投影，在这种坐标系统下，仍然将边长归算到参考椭球面上,但投影带的中央子午线是选能补偿高程归算引起的长度变形的某一条子午线作为测区的中央子午线.由式（3）得，任意带法只适用于Hm＞0的区域，则任意带中央子午线的选取如下[6-9]：

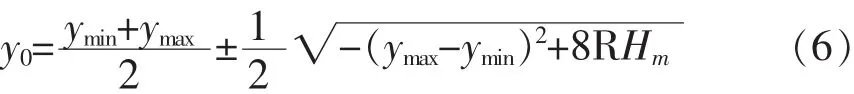
当（ymax-ymin）2≥4RHm，且Hm/R≤1/104，此时平移后中央子午线位于测区内，

（3）综合以上两种方法，同时改变Hm及ym，抵偿两项归算改正变形，即带有高程抵偿面的任意带高斯正形投影.

根据抵偿任意带高斯投影平面坐标系选择[10-12]思想，按最小二乘原理与求函数平均值，在[VSVS]最小前提下选取抵偿面和抵偿点，令ΔS1,1=ΔS1,2=…=ΔS1,n.

于是公式（3）可改为

根据最小二乘法原理

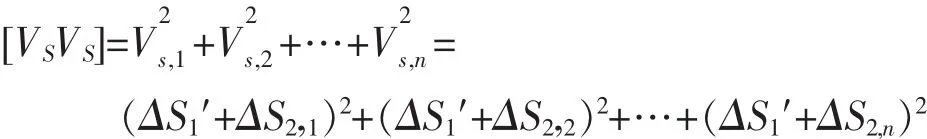
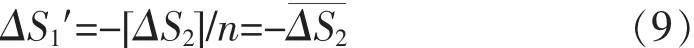
根据定积分中值定理对公式（2）求平均值

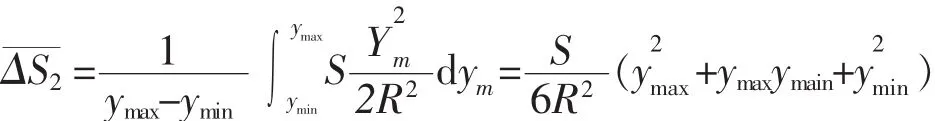
于是

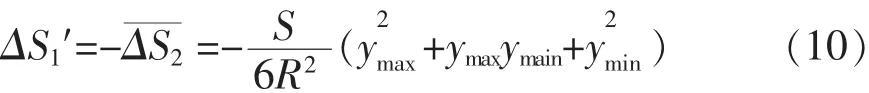
将公式（2）和公式（10）代入公式（3）中,可得长度综合变形

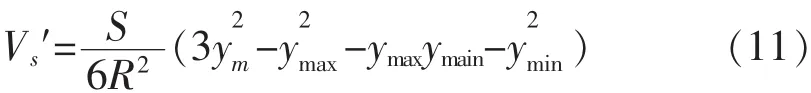
将公式（10）代入中算出抵偿高

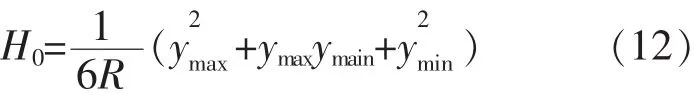
则抵偿高程面的高程Hm’为（Hm-H0）.将公式（10）代入公式（2）中，得

上式中，若ymain与ymax分别为0时，有

2 工程验算实例

2.1 测区概况

某高速公路项目东西跨距较长，海拔较高，测区范围基本位于北纬25°32′到25°47′之间，东经113°24′～114°20′之间，主线全长120 km,在1956年黄海高程系统下，全线高程在300 m至900 m之间，地势起伏大,相对高差最高达550 m,测区相对于参考椭球面的平均高程Hm=552 m.当中央子午线为114°时，y∈（-50，35）km.选择常规坐标系解算结果无法满足工程精度要求，分别利用国家标准分带直角坐标系、带抵偿投影面坐标系、任意带高斯投影坐标系、带抵偿投影面的任意带高斯投影坐标系进行计算分析，获得满足工程需要的最优方案.

2.2 测区坐标系统选择

2.2.1 国家3°带高斯正形投影平面直角坐标系统

若测区控制网直接采用1954年北京坐标系3°分带,则由公式（3）计算，测区内每公里投影长度变形统计见表1（只选取测区部分坐标）.

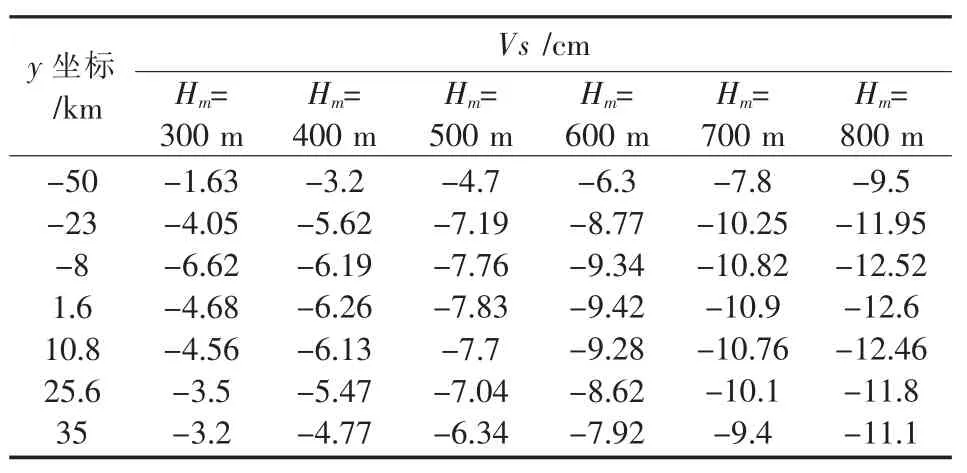
表1 北京54坐标系下测区每公里投影变形统计表

由表1数据可知，测区每公里投影长度变形值在（-12.6 cm，-1.63 cm）之间.大部分区域长度变形远大于2.5 cm，可见该测区不宜直接采用国家3°带高斯正形投影平面直角坐标系.

2.2.2 抵偿投影面的3°带高斯正形投影平面直角坐标系

相应的抵偿高程面为H=552-56=496 m.

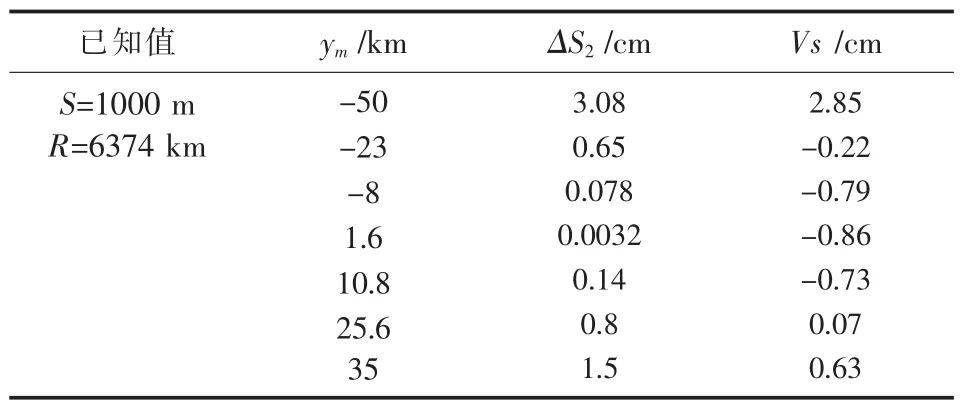
表2 测区每公里投影变形统计表

由表2数据可得，测区每公里投影长度变形值在（-0.86 cm，2.2 cm）之间，能满足规范所规定不超过2.5 cm／km的要求,此坐标系可以满足本项目测量要求.

2.2.3 任意带高斯正形投影平面直角坐标系

根据1.2节，由于（35+55）2=8100≤4 RHm，所以由式（1.6）得，y0=64 km，即测区向东移64 km.

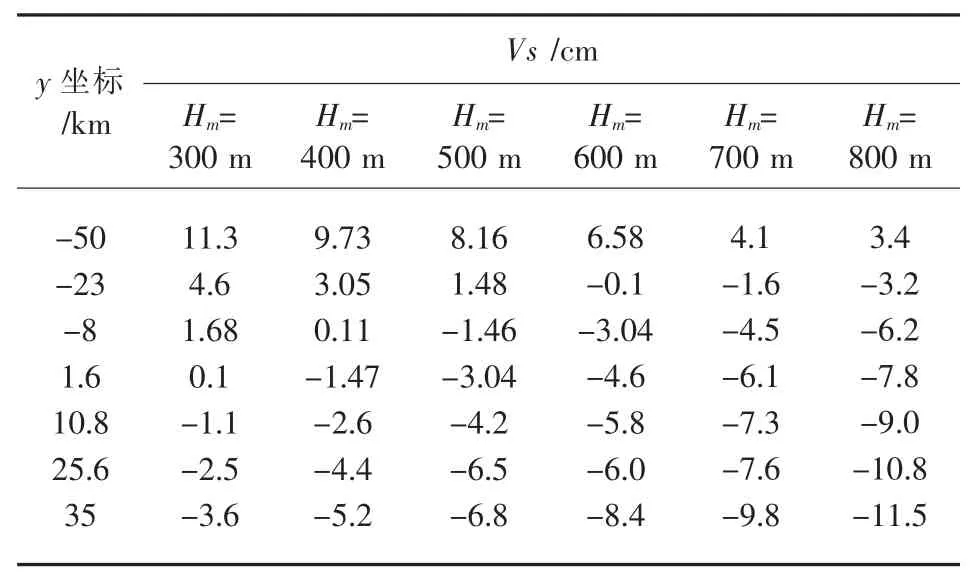
表3 测区每公里投影变形统计表

在表3中，测区每公里投影长度变形值在（-11.5 cm，11.3 cm）之间，绝大部分都不能满足不超过2.5 cm／km的规范要求.因此，任意带高斯正形投影平面直角坐标系并不能满足本项目的测量要求.

2.2.4 抵偿高程面任意带高斯正形投影平面直角坐标系

这种坐标系是2.2.2与2.2.3所述坐标系的综合,既改变投影面又改变了中央子午线的位置，更能有效地实现两种长度变形改正的补偿.设S=1000 m,R=6371 km，由1.2节可得，根据测区数据可得

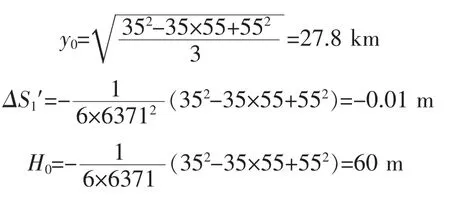
下面表4为采用此坐标系后每公里的投影变形值.

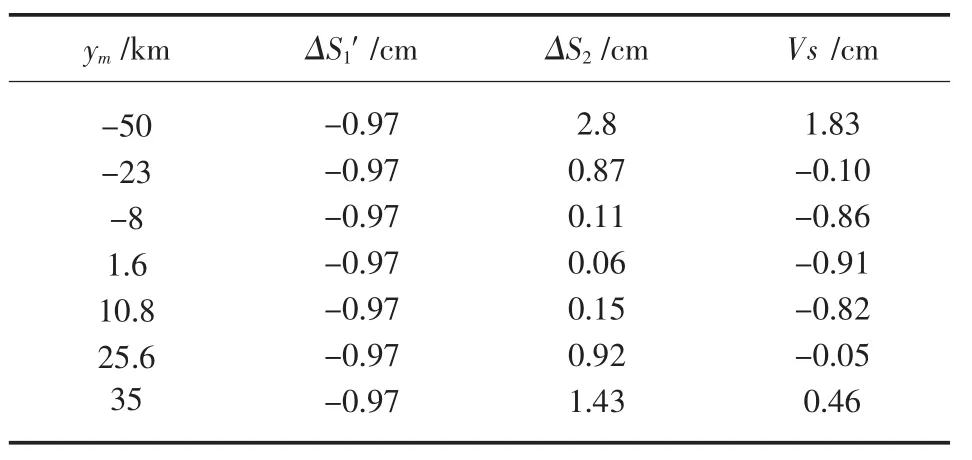
表4 测区每公里投影变形值

由表4知，测区每公里投影长度变形值不大于2.5 cm／km，位于（-0.91 cm,1.83 cm）之间，能满足规范要求，并且比抵偿投影面的3°带高斯正形投影平面直角坐标系更能有效地抵偿测区的长度变形.因此，采用投影抵偿面和改变投影子午线相结合的方法，投影长度变形值可以很好地相互抵消.

3 小结

（1）对于跨距较大且海拔较高地区的线路工程，限制长度变形最有效的办法是：依据线路工程测区范围,选择测区中央位置为投影带中央子午线,并且采用抵偿投影.

（2）长距离线路工程要充分考虑长度投影变形值的影响,设计合理的测量坐标系来消除或减弱其影响,以保证线路工程建设的精度.

[1]孔祥元.控制测量学(下)[M].武汉：武汉大学出版社，2006.

[2]麦春.兰勃特投影在铁路工程独立坐标系设计中的应用[J].高速铁路技术，2011，2(2)：22-24.

[3]刘陶胜，黄声享，罗力，等.基于重心基准的平面坐标转换研究[J].大地测量与地球动力学，2011，31(2)：102-105.

[4]曾宪珪，罗力.GPS控制网加入常规观测值对网精度的影响[J].江西理工大学学报，2006，27(4)：12-14.

[5]范一中.再谈工程投影面的最佳选取问题[J].测绘通报，2003(8)：46-47.

[6]薛晓轩，鲁彩娟，秦闻宇.城市坐标系的选择与抵偿计算[J].测绘与空间地理信息，2010，33(7)：187-189.

[7]俞建康，蒋惠新.长线路测量坐标系建立与GPS的应用[J].现代测绘，2011，34(3)：34-36.

[8]林全胜.工程测量中坐标系的选择思路与方法研究[J].科技资讯，2010(36)：40.

[9]黄崇国.公路测量中坐标系统确定方法的探讨[J].技术与市场，2011，18(8)：165-166.

[10]范一中，赵丽华.任意带高斯正形坐标系的最佳选取问题[J].测绘通报，2000(8)：7-8.

[11]陈顺宝，任建春，亓月，等.抵偿任意带高斯投影平面坐标系选择的研究[J].测绘通报，2005(7)：21-23.

[12]方杨.任意带任意投影面的平面坐标转换方法研究[J].铁道勘察，2011(3)：18-20.

Analysis of deformation control on long-distance projection

LI Pei-hong，WANG Fu-qi，LIU Tao-sheng

(School of Architectural and Surveying&Mapping Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China)

According to the length deformation theory of the projection,the farther away from the coordinate origin,the greater equidistant deformation values.In a long line project,how to properly select the coordinate system is fully considered to reduce the projection distortion and improve the accuracy of the control network solver.For a highway,the relationship between the length deformation of line project and the choice of coordinate system is analyzed,then the projection distortion value in a variety of coordinate systems is calculated,Finally,arbitrary zone Gaussian projection coordinate system with offset elevation surface is built comparatively,all of which could eliminate or reduce the length deformation of the control network effectively,through the analysis of calculation results.

Projection length deformation；coordinate system；compensation projection

P58

A

2012-02-26

江西省教育厅科技资助项目（GJJ11473）

李沛鸿（1964-），男，教授，主要从事测绘科学与技术等方面的研究，E-mail：jxlgdlph@126.com.

2095-3046（2012）03-0034-04