基于单模数多变量二次同余方程组设计的密码体系

严深海

（赣南师范学院数学与计算机科学学院，江西赣州341000）

基于单模数多变量二次同余方程组设计的密码体系

严深海

（赣南师范学院数学与计算机科学学院，江西赣州341000）

研究两类含项的单模数多变量二次同余方程组的求解方法及其在设计密码体系中的应用.针对p≡3 mod 4研究得到了多变量二次密码体系MVQC（Multivariate Quadratic Cryptography），给出了数值算例，算例说明所设计的密码体系是可行的，鉴于交互确认的解密策略，密码体系是安全的.

二次同余；多变量；密码体系；MQ-Schemes

0 引言

设计多变量密码体系的思路是使用特殊的非线性多项式函数组，它的安全性基础是一个已被证明的定理，即求解有限域上的2次以上的多元多项式方程组是一个NPC问题[1].多变量密码体制被许多密码学家认为具有效率高和抗量子计算机攻击的优点[2-3]，是未来量子计算时代密码的备选方案之一，因此备受关注.目前，研究了含xixj而不含项的单模数多变量二次同余方程组的求解方法及依其设计了密码体系的有文献[4、5、6]，研究了含xixjxk而不含、项的单模数多变量三次同余方程组的求解方法及依其设计了密码体系的有文献[5]，文献[7、8、9]研究了含xixjxkxl的单模数多变量四次同余方程组的求解方法及其应用，尚未见含项情形的报道.

文中研究两类含x2i项的单模数多变量二次同余方程组的求解方法及依其设计密码体系，特别是模数p≡3 mod 4时的情形.具体来说，文中研究以下单模数多变量二次同余方程组的求解方法及其在设计密码体系中的应用：

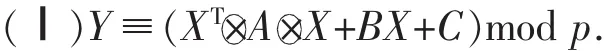
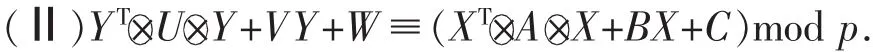
这里，p为素数，X=（x1，x2，…，xn）T，Y=（y1，y2，…，yn）T，xi，yi∈{0，1，…，p-1}，A=（A1，A2，…，An）T，U=（U1，U2，…，Un）T，C=（c1，c2，…，cn）T，W=（w1，w2，…，wn）T，wi，ci∈{0，1，…，p-1}，XTAX=（XTA1X，XTA2X，…，XTAnX）T，YTUY=（YTU1Y，YTU2Y，…，YTUnY）T，其中

特别地，在方程组Ⅰ、Ⅱ中取n=1时，各自对应的方程为

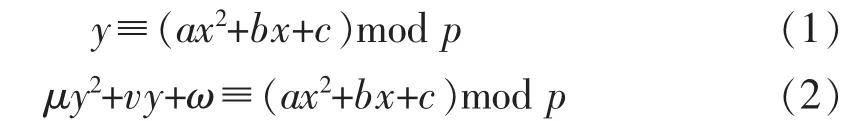
这里，μ，v，ω，a，b，c∈{0，1，…，p-1}.

上述问题属于MQ(Multivariate quadratic)问题，该类问题通常表述为：

f1（x1，x2，…，xm，y1，y2，…，yk）≡0 mod p,…，fn（x1，x2，…，xm，y1，y2，…，yk）≡0 mod p，这里fi（x1，x2，…，xm，y1，y2，…，yk）为以x1，x2，…，xm，y1，y2，…，yk为变量的二次多项式[4].基于这类问题得到的密码体系通常记为MQ—Schemes[4].目前，研究较成熟的是“可线性化的二次问题”：

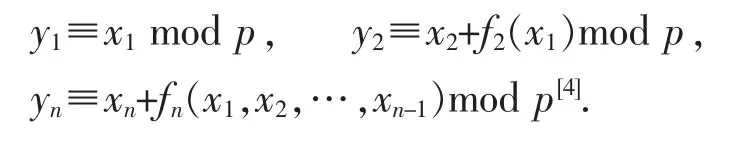
1 方程组I的求解及其在密码体系设计中的应用

本节首先讨论单个方程（1）的求解，然后得到方程组I的求解及其应用.

引理1[10]当a≠0，（a，p）=1，方程（ax2+bx+c）≡0 mod p与（x-x0）（x-x1）≡0 mod p等价时，有解x0和x1.

引理2[10]当a≠0，（a，p）=1，方程（ax2+bx+c）≡0 mod p与Z2≡c0mod p等价，这里，Z=x+（2a）-1b,c0=（b2-4ac）（4a2）-1.

引理3[10]当p≡3 mod 4c0mod p有解，且解的表达式为

于是，基于单个方程y≡（ax2+bx+c）mod p可设计密码体系(简记为MVQC-1)如下：

系统设置：甲方选择整数a，b和c及p≡3 mod 4且传（a，b，c，p）给乙方.

加密：当乙方要传送信息x给甲方时，乙方找出甲方的密钥（a，b，c，p），通过式（1）计算出y*≡（ax2+bx+c）mod p，且传y*给甲方.

解密：当甲方收到乙方传来的信息y*，通过解方程（ax2+bx+c）mod p≡y*，可得到解x0、x1.于是从x0、x1中选定一个确认为乙方送给甲方的信息x*.

再则，研究方程组I知其有以下等价式：

定理1考虑到矩阵A、B的特殊结构，方程Y≡（XTAX+BX+C）mod p等价为：

定理2进一步考虑到Ai的特殊结构，方程Y≡（XTAX+BX+C）mod P等价为：

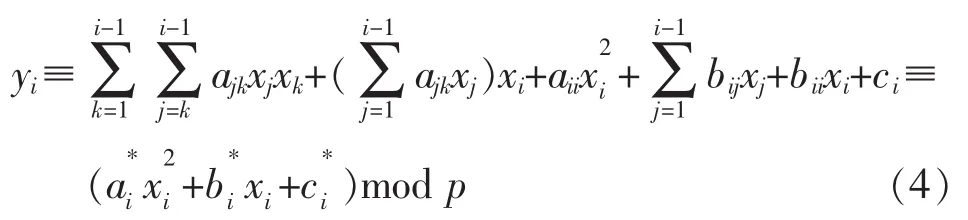
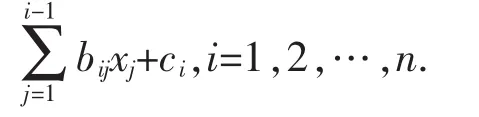
于是，根据方程组I对应的式（3）和（4）可设计密码体系(简记为MVQC-2)如下：

系统设置：甲方选择矩阵Ak（k=1，2，…，n），B和C及p≡3 mod 4，且传送给乙方.

加密：当乙方要传送信息X给甲方时，乙方找出甲方的密钥（Ak，B，C，p），通过式（3）计算出Y*≡（XTAX+BX+C）mod pY*给甲方.

解密：当甲方收到乙方传来的信息Y*，通过式（4）逐次解单元方程：

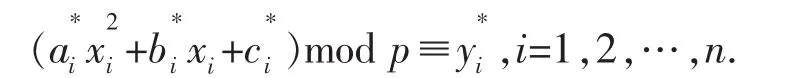
得解xi0和xi1，从而同一密文Y*有与之对应的2n个解Xi=（x1，x1，…，xn）T，这里xi=xi0或xi1.将所有解按字典顺序排列，则解与其序号有唯一对应关系.

唯一明文的确定：

乙方：根据信息Y*，通过式（4）逐次解单元方程：

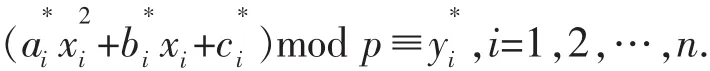
甲方：根据乙方传的数据i，在解Xi的排序方案中找到对应的信息X，得到唯一明文.

2 方程II的求解及其在密码体系设计中的应用

本节首先讨论单个方程（2）的求解，然后得到方程组II的求解及其应用.容易基于单个方程μy2+vy+ω≡（ax2+bx+c）mod p设计密码体系(简记为MVQC-3)如下：

系统设置：设素数p为通信双方预先约定的.当甲乙双方需要通信时，临时建立方程，且甲方选择整数（a，b，c）且传送给乙方；乙方选择整数（μ，v，ω）且传送给甲方.

加密：当乙方要传送x给甲方时，乙方找出甲方传给的数据（a，b，c），计算x*≡（ax2+bx+c）mod p，乙方求解方程μy2+vy+ω≡x*mod p得y0和y1，乙方将y=y0或y1传送给甲方.

解密：当甲方得到乙方传来的数据y时，甲方找出乙方传送的数据（μ，v，ω），计算y*≡（μy2+vy+ω）mod p，且求解方程（ax2+bx+c）≡y*mod p得x0和x1，甲方视x0或x1为乙方要传送给甲方的信息.

再则，研究方程II知其有以下等价式：

定理3考虑到矩阵U，V，A，B的特殊结构，方程II可整理为：

定理4进一步考虑到Ui，Ai的特殊结构，方程（5）可表示为：

这时，

于是根据式（5）（6）可设计密码体系(简记为MVQC-4)如下：

系统设置：设通讯双方有共同约定的大素数p，且p≡3 mod 4.甲方选择矩阵Ai，构造出A，且选择B和C，且传送（A，B，C）于乙方；乙方选择矩阵Ui，构造出U，且选择V和W，且传送（U，V，W）于甲方.

加密：当乙方要传送信息x给甲方时，For i=1，2，…，n，乙方找出甲方传的三元组数据（A，B，C），由式（6）计算n；乙方根据自己选定的（U，V，W）求解方到yi=yi0，yi1；乙方将最多2n个可行解中的任一个传给甲方.

解密：当甲方得到乙方传来的数据Y时，甲方找出乙方传的三元组（U，V，W），由式（6）计算方根据自己选定的（A，B，C），求解方此时2n个解按字典顺序排列，所有解有唯一序号.

唯一明文的确定：

乙方：根据信息Y*，通过式（6）逐次解单元方程：

甲方：根据乙方传的数据i，在解Xi的排序方案中找到对应的信息X，从而得到唯一明文.

3 数值算例

以密码体系MVQC-1、MVQC-4为例，说明文中得到的密码体系是信息冗余、可行、安全：

例1设通讯双方约定素数p=107，试由密码体系MVQC-1实现：乙方将信息x=71传送给甲.

解：系统设置：甲方选择整数（a，b，c）=(86，16，46)且传送给乙方.

加密：乙方欲将信息x=71传送给甲方，则乙方计算出y*≡（ax2+bx+c）mod p≡（86*712+16*71+46）mod 107≡74 mod 107，且将y*传送给甲方.

解密：当甲方得到乙方传来的数据y*时，则甲方由ax2+bx+c≡y*mod p即86x2+16x+46≡74 mod 107可反解出x0=71，x1=103，于是从x0、x1中选定一个确认为乙方送给甲方的信息x.

例2设通讯双方约定素数p=107，试由密码体系MVQC-4实现：乙方将信息X=（66，98，98，64，36）T传送给甲.

解：系统设置：甲方选择矩阵Ak（k=1，2，…，5），B以及向量C如下，并将之传送给乙方；

乙方选择矩阵Uk（k＝1，2，3，4，5）、V及向量W如下，并将之传送给甲方.

加密：乙方欲将信息X=（66，98，98，64，36）T传给甲方时，则乙方：

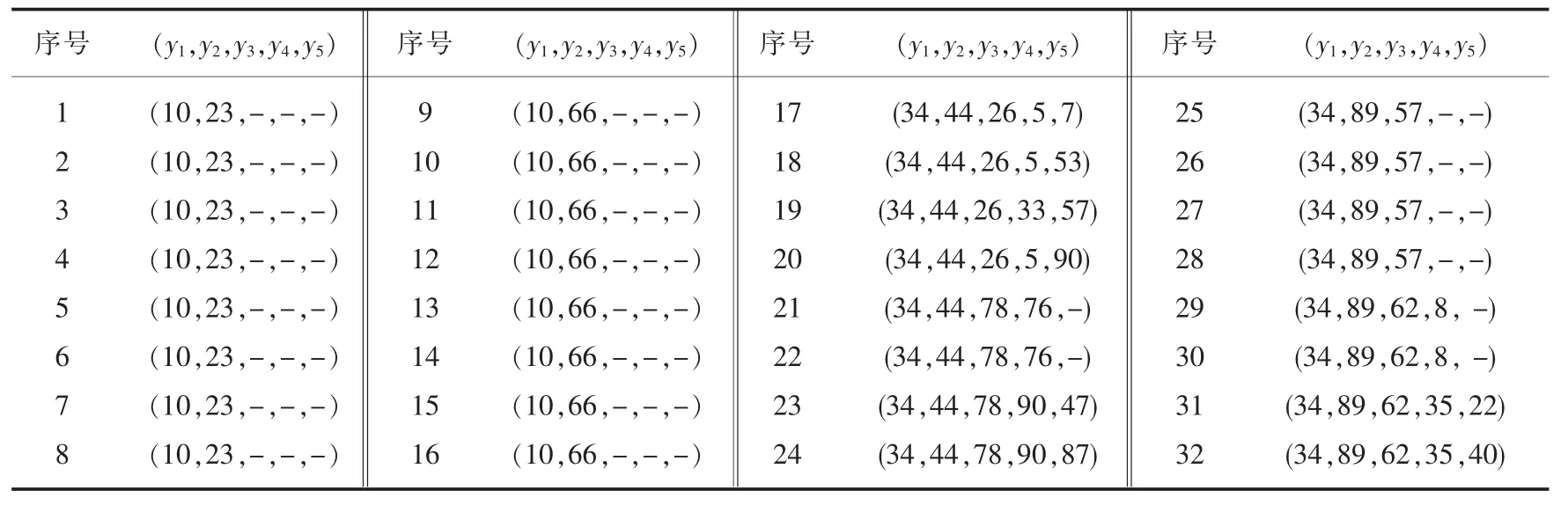
表1 Y所有可能的解（表中“-”标识无解）

1）由X计算出X*≡（XTAX+BX+C）mod P≡（46，42，58，89，101）Tmod 107；

2）再由X*通过方程YTUY+VY+W≡X*mod p解出Y（见表1）；

3）乙方将上表中Y=(34，44，26，5，53)传给甲方.

解密：当甲方得到乙方传来的数据Y（向量）时，则甲方：

1）计算Y*≡（YTUY+VY+W）mod P≡（46，42，58，89，101）Tmod 107；

2）求解方程（XTAX+BX+C）mod P≡Y*得X（见表2）.

唯一明文的确定：

表2 X所有可能的解（表中“-”标识无解）

甲方：根据乙方传的数据i=19，在解的排序方案中找到对应的信息X=（66，39，36，104，32），从而得到唯一明文.

综上所述，文中研究了两类特殊结构的多变量二次同余方程组的求解及其在密码体系设计中的应用.所设计的密码体系采用了一种特殊的矩阵结构和多变量二次同余式，能获得较高安全性.再加上从按字典排序排列的2n个解中，双方在传递信息的同时要临时确定一序号才能得到传送准确的信息，解的多样性，信息的冗余性，也增添了密码体系传送信息的安全性.

[1]DingJ，GowerJE，SchmidtDS.Multivariatepublickey cryptosystems[M].Berlin：Springer-Verlag Press，2006.

[2]Shor P W.Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J].SIAM Journal on Computing，1997，26(5)：1484-1509.

[3]王鑫，刘景美，王海梅.多变量签名模型的改进[J].北京邮电大学学报，2009，32(5)：124-127.

[4]Wang L C，Yang B Y，Hu Y H，et al.A“Medium-Field”multivariate public-key encryption scheme[J].Lecture Notes in Computer Science，2006(3860)：132-149.

[5]Tsutomu Matsumoto，Hideki Imai.Public quadratic polynomialtuples for efficient signature-verification and message-encryption[J].Lecture Notes in Computer Science，1988(330)：419-453.

[6]林殊芳，汤绍春.一类带有冗余信息的Hill密码体系[J].江西理工大学学报，2010，31(3)：60-63.

[7]李文锋.基于RSA和Hill密码体系的文件加密系统的研究和实现[D].赣州：江西理工大学，2007.

[8]王志伟，郑世慧，杨义先，等.改进的Medium-Field多变量公钥加密方案[J].电子科技大学学报，2007，36(6)：1152-1154.

[9]田礼，鲍皖苏.MFE多变量公钥改进方案分析[J].计算机工程，2010，36(18)：155-157.

[10]赖溪松，韩亮，张真诚.计算机密码学及其应用[M].北京：国防工业出版社，2001.

A cryptosystem based on multivariate quadratic equations with single modulus

YAN Shen-hai

(College of Mathematics and Computer Science，Gannan Normal University，Ganzhou 341000，China)

The article studies the solutions to two types of single modulus multivariate quadratic equations including itemand their applications in the designment of cryptosystems.We get the multivariate quadratic cryptosystem(MVQC)by studyingand give some numerical examples.The examples demonstrate MVQC's feasibility.Given decryption strategy with interactive confirmation,MVQC is a secure encryption scheme.

quadratic congruence;multivariate；cryptosystem；MQ-Schemes

TN918.1

A

2012-02-29

江西省科技厅科技支撑计划项目（2009ZDG03600）

严深海（1972-），男，讲师，主要从事算法设计、图像处理等方面的研究，E-mail：gnsyysh@126.com.

2095-3046（2012）03-0076-05