股市指数日间变化与夜间跳跃关系的非参数计量研究

赵钊

(上海交通大学安泰经济与管理学院，上海200240)

股市指数日间变化与夜间跳跃关系的非参数计量研究

赵钊

(上海交通大学安泰经济与管理学院，上海200240)

运用非参数统计分析方法，研究股市指数夜间跳跃与日间变化之间的关系;基于R软件，采用基本统计量、散点图与拟合函数图，对全球范围内7个股票交易市场的每日交易数据进行分析;以上证综合指数为例，通过渐进正态分布和Bootstrap置信带分析，得到夜间跳跃和日间变化拟合度较高的百分比夜间跳跃区间，依据区间内夜间跳跃和日间变化的关系，提出了基于夜间跳跃的股市可获利交易策略。分析认为:夜间跳跃和日间指数变化存在相关关系;在不同的股票市场，其相关关系不同;技术分析对指导股票市场的投资是有效的。

非参数统计;股市指数;置信带;可获利投资策略

在观察股市指数时会发现，股市指数不仅在每天的交易时间内不断地变化(日间变化)，而且每个交易日的开盘指数与上一个交易日的收盘指数之间也有一个差值(夜间跳跃)。股市指数的日间变化和夜间跳跃从不同侧面反映了各个产业、市场的各种金融变化讯息，在本质上有着内在的联系。运用数理统计的方法，研究股市日间变化和夜间跳跃之间的关系，从而提出股市可获利交易策略，具有重要的实际应用意义。

对股票市场的分析，主要分为技术分析和基本分析。技术分析是指研究过去金融市场的资讯，并结合统计分析方法来预测股票价格的趋势与决定投资的策略，分析股市日间变化与夜间跳跃之间的关系进而提出投资策略。技术分析作为最早的投资分析方法，可追溯到19世纪末的道琼斯理论。然而，许多金融经济学家认为技术分析在预测股票价格方面不具有效性，因为他们认为股票价格是随机游动的，投资者利用技术分析无法预测股票价格，如Fama等认为技术分析对股票市场是有效的，即股票价格已充分反映了所有相关的信息，利用技术分析并不能获得超额报酬［1-2］。然而，Brock等以1897年第一个交易日至1986年最后一个交易日道琼斯工业平均指数为研究对象，利用简单技术分析交易规则，如移动平均线法、阻力线法、支撑线法，结果发现技术分析有助于预测道琼斯工业平均指数［3］。自此以后，许多学者探讨技术分析交易规则是否有助于预测各国股票价格［4-6］，研究结果表明，技术分析对股票市场是有效的。

笔者以全球范围内7个股票交易市场从2005年1月1日之后第一个交易日开始至2012年4月25日的每日交易数据为研究对象，运用非参数统计分析方法，研究股市指数夜间跳跃与日间变化之间的关系，并以上证综合指数的分析为例，依据百分比夜间跳跃区间内，夜间跳跃和日间变化的关系，提出了基于夜间跳跃的股市可获利交易策略。

一、非参数回归理论

回归模型分为参数回归模型和非参数回归模型。参数回归模型的回归函数形式都是预先设定的，只是其中的未知参数需要估计，这一类回归模型最大优点是回归结果可以外延，模型的参数一般都有明确的经济意义，当然这一切需要具有很明确的前提条件，即回归模型的假设成立。如果回归模型及参数的假定与实际情况相背离时，推断和预测就会有较大的偏差，拟合效果也会很差，甚至没有什么实际意义。因此，参数回归模型缺乏稳健性。与参数回归模型相反，非参数回归模型的回归函数形式是未经设定的，其形式约束较少，解释变量与被解释变量的分布也很少限制。因此，它具有更大的适应性。

由于股市指数受各方面因素影响，对选取的样本数据不能确定其符合某一种既定分布，不能用传统的参数统计方法进行数据的分析，所以，非参数计量方法更适合对股市指数数据进行处理与分析。

(一)非参数回归函数与真实函数的一致性

一致性是估计量最基本的属性。设有变量X，其中包含数据xi(i=1，2，3，…，n)，X的真实函数为f(x)。取X的一部分数据x1，x2，x3，…，xn进行非参数回归拟合，得到的拟合函数为^f(x)。以下说明当n→+∞时，^f(x)→f(x)，即非参数回归函数与真实函数具有一致性需要满足的条件。

根据文献［7］有:

假设1:观测值x1，x2，x3，…，xn满足独立同分布;

假设2:当n→+∞时，h=hn→0，其中h为带宽，h为n的函数，当n→+∞时，h→0;

假设3:当n→+∞时，nhn→+∞;

假设4:K为Borel可测有界实值函数，Ψ为K的变量，且同时满足:

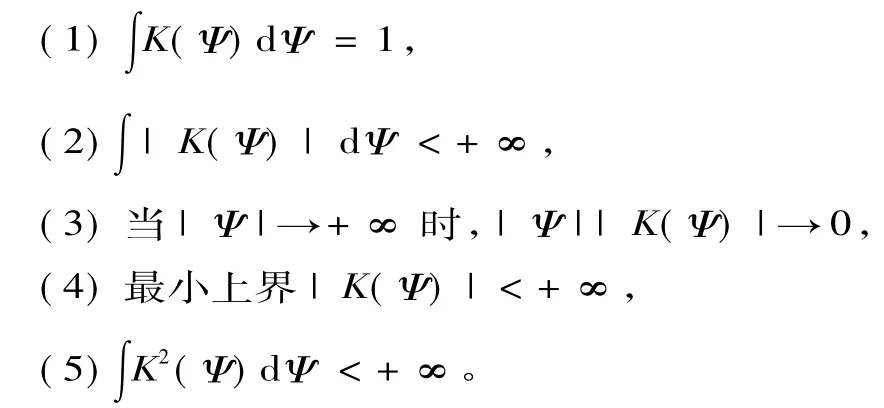
假设5:在任意一点x0，f(x)连续，且∫|f(x)|·dx＜+∞。

在现实操作中，经济数据不可能是独立同分布的，假设1就不成立了。而当所用数据是时间序列数据时，不要求数据独立同分布，假设1也成立。

定理1:当假设1～5满足时，^f(x)与f(x)具有弱式一致性，即当n→+∞时，概率P［|^f(x)－f(x)|＜ε］→1，ε→0。

定理1说明了在数据量足够大时，非参数拟合得到的拟合函数趋向于真实函数。

(二)置信带的构建

1．渐进正态分布方法构建置信带

现在假设有数据(yi，xi)(i=1，2，3，…，n)，变量yi和xi的非参数回归模型为

式中:m(xi)为回归函数;ui为回归函数与真实函数之间的差值，即残差，且ui满足独立同分布。

根据文献［7］有:

假设6:当n→+∞时，h=hn→0，nhn→+∞;

假设7:xi独立同分布且与残差独立;

假设8:同假设4;

假设9:期望E|ui|2+σ＜+∞，且存在σ＞0，使得∫|K(Ψ)|2+σdΨ＜+∞，其中σ为标准差。

2．Bootstrap方法构建置信带

除了渐进正态分布方法，另外还有一种Bootstrap方法可以用来构建置信带，且受到了更多的关注。将数据x1，x2，x3，…，xn重新排序j次，得到j组重新排序的数据，…，用第j组数据做回归，因为数据只是重排，并没有改变，所以拟合函数^fj(x)的期望E［^fj(x)］=^f(x)，再用上面的方法求得的置信带是对应于期望E［^f(x)］(而不是f(x))的置信带。这时直接用真实值和回归值之间的差值，即可求得对应于f(x)的置信带，这就是Bootstrap构建置信带的方法。根据文献［7］的分析，Bootstrap的范围误差比渐进正态分布的要小。

二、数据的处理与分析

(一)基本统计量分析

笔者对全球7个股票市场，即上证综合指数、深圳成分股指数、道琼斯指数、纳斯达克指数、德国指数、日经指数和香港恒生指数，从2005年1月1日之后第一个交易日开始至2012年4月25日的每日交易数据进行分析(数据来源为雅虎金融数据库)。数据包含7个项目，分别为交易日期、开盘价、最高价、最低价、收盘价、成交量和调整后收盘价。

每日开盘价Oi与上一个交易日的收盘价Ci－1和自变量夜间跳跃Pi的关系为

每日调整后收盘价Ci与当日的开盘价Oi和因变量指数变化Ei的关系为

夜间跳跃和日间变化的基本统计量见表1、2。由表1、2可知:夜间跳跃和日间变化的平均值聚集在0附近;根据夜间跳跃和日间变化的标准差分析，深圳成分股指数在这7支指数中是最不稳定的指数，相对而言，上证综合指数在这7支指数中是比较稳定的;香港恒生指数夜间跳跃和日间变化的峰度都小于3，说明其是变化比较平缓的指数。

表1 夜间跳跃基本统计量

(二)非参数回归分析

对7个股票市场的夜间跳跃和日间变化数据，运用Local-Linear非参数回归分析，得到7个股票的数据量、带宽、剩余标准差和判定系数R2(R2表示夜间跳跃和日间变化之间的相关性)，见表3。

由表3可知，带宽从小到大排序为上证综合指数、纳斯达克指数、深圳成分股指数、道琼斯指数、日经指数、香港恒生指数、德国指数，带宽越大，回归函数越平滑，但也越不精确。剩余标准差表示拟合值和真实值之间的差值，其值越小，拟合精度越好。由表3可知:纳斯达克指数拟合精度最好，香港恒生指数最差，上证综合指数的相关性最高，R2=0．351 027。

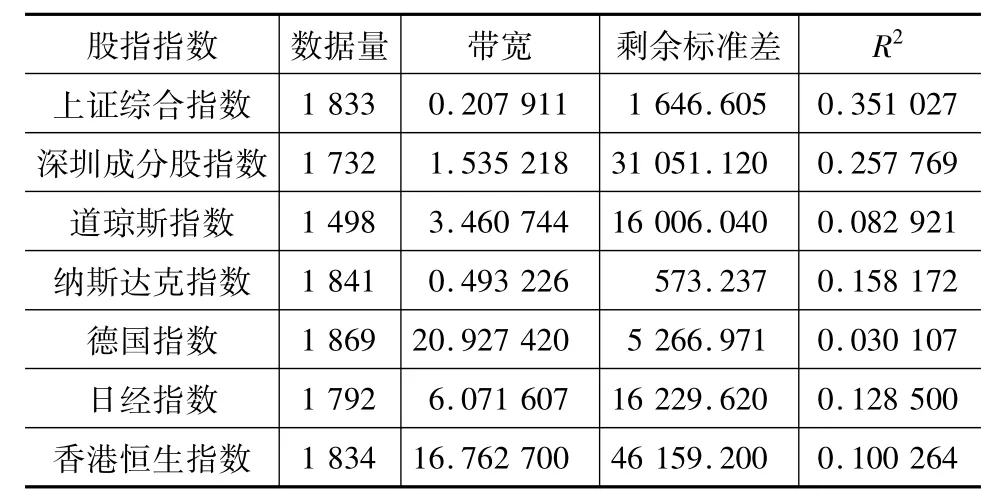
表3 各股市非参数回归数据

1．散点图和拟合函数图

运用R软件［8］，绘制各股票市场夜间跳跃和日间变化的散点图和拟合函数图［9-10］，见图1、2。

7个股市的散点图基本分为3个类型。上证综合指数、道琼斯指数的散点图(图1(a))呈“十”字型，表明在夜间跳跃的特定区间内，夜间跳跃和日间变化的关系较为明显;而日经指数的散点图(图1(b))呈“一”字型，这是由于日本的许多经济政策跟随美国而变动，美国市场上的信息会对日本市场造成影响，在夜间跳跃中已经反映了一些信息，所以在日间指数变化中所反映的信息量就减少了，反映在图上就是扁平状;其余4个股市的散点图呈“球”型，表明夜间跳跃和日间变化的关系不显著，也可看作是市场比较有效。纵观7个股市夜间跳跃和日间变化的拟合函数图，可以看到在夜间跳跃为0的邻域，上证综合指数和道琼斯指数日间变化随夜间跳跃的变化起伏明显，说明夜间跳跃对日间变化影响显著;日经指数日间变化随夜间跳跃变化起伏不大，说明夜间跳跃对日间变化有影响，但影响不显著;其余4个股市，日间变化基本不随夜间跳跃的变化而变化，说明夜间跳跃对日间变化没有影响。夜间跳跃对日间变化的影响区域，不仅反映了拟合函数的带宽，也反映了各个股票市场上2个变量拟合程度较高的区域。

2．置信带

由上述分析可知，上证综合指数夜间跳跃和日间变化关系较为明显，相关性最高(R2=0．351 027)，因此，选择上证综合指数为研究对象，通过置信带(区间)分析，确定夜间跳跃和日间变化拟合度较高的区域。为了便于比较，需要将夜间跳跃和日间变化的值百分比化，即分别用夜间跳跃和日间变化除以当日收盘价再乘以100得到新的变量:百分比夜间跳跃和百分比日间变化，然后用新变量做非参数回归分析。分别用渐进正态分布和Bootstrap方法求置信带，并比较在2种置信带方法下拟合度较高的夜间跳跃区间［11-13］。

按上述思路将股票市场的数据进行处理，处理后的数据如表4所示。

采用渐进正态分布和Bootstrap方法分别计算股票市场置信带，调整百分比夜间跳跃的范围，得到拟合程度较高，即接近日间变化为0的区间的图见图3、4。

图1 夜间跳跃和日间变化的散点图

图2 夜间跳跃和日间变化的拟合函数图

由图3、4可知:百分比日间变化为0时，说明不论百分比夜间跳跃如何变化，都影响不到百分比日间变化，则百分比夜间跳跃与百分比日间变化没有显著关系。在置信带图中，作百分比日间变化为0的直线，凡置信带包含直线百分比日间变化为0的区间，百分比夜间跳跃与百分比日间变化没有显著的关系;反之，置信带没有包含直线百分比日间变化为0的区间，百分比夜间跳跃与百分比日间变化有显著关系［14-15］。

由图3、4还可知:在区间(－3．5，－2．5)、(0．2，1)和区间(－3．2，－2．5)、(0，1)内日间变化与夜间跳跃有显著关系，其交集为(－3．2，－2．5)、(0．2，1)。依此，可以观察每日的夜间跳跃数据，当其处于此区间中时，根据此区间内日间变化与夜间跳跃的关系，决定买入/卖出上证综合指数基金或等价的股票组合，以达到获利目的。当夜间跳跃不在此区间时，不存在基于夜间跳跃的可获利交易策略。

表4 数据百分比化处理

三、结语

运用非参数回归分析方法，对全球7个股票市场夜间跳跃和日间指数变化之间关系进行研究。夜间跳跃和日间指数变化存在相关关系，在不同的股票市场，其相关关系不同。通过渐进正态分布和Bootstrap置信带分析，可获得夜间跳跃和日间变化拟合度较高的百分比夜间跳跃区间，依据区间内夜间跳跃和日间变化的关系，预测股市指数的变化趋势，从而制定基于夜间跳跃的股市可获利交易策略。由此说明，技术分析对指导股票市场的投资是有效的。从理论上来讲，本文研究方法也适用于其他股市和个股的投资。

［1］Fama E F．Efficient capital markets:a review of theory and empirical work［J］．The Journal of Finance，1970，25(2):383-417．

［2］Fama E F，French K．The cross-section of expected stock returns［J］．The Journal of Finance，1992，47(2):427-465．

［3］Brock W，Lakonishok J，LeBaron B．Simple technical trading rules and the stochastic properties of stock returns［J］．The Journal of Finance，1992，47(5):1731-1764．

［4］Bessembinder H，Chan K．The profitability of technical trading rules in the Asian stock markets［J］．Pacific-Basin Finance Journal，1995，3(2):257-284．

［5］Hudson R，Dempsey M，Keasey K．A note on the weak from efficiency of capital markets:the application of simple technical trading rules to UK stock prices from 1935 to 1994［J］．Journal of Banking and Finance，1996，20(6):1121-1132．

［6］Parisi F，Vasquez A．Simple technical trading rules of stock returns:evidence from 1987 to 1998 in Chile［J］．Emerging Markets Review，2000，1(2):152-164．

［7］Pagan A，Ullah A．Nonparametric econometrics［M］．Cambridge:Cambridge University Press，1999．

［8］Hayfield T，Racine J S．Nonparametric econometrics:the np package［J］．Journal of Statistical Software 2008，27(5):1-32．

［9］范依梅．“有效市场假说”综述［J］．集团经济研究，2007(9Z):266．

［10］戴丽娜．非参数技术理论及应用综述［J］．新乡学院学报:自然科学版，2008:25(3):14-17．

［11］张锐力，董彦峰．有效市场假设及其检验方法:文献综述［J］．现代营销:学苑版，2011(8):84-85．

［12］张晨曦，姜姣娇．有效市场假说的理论综述［J］．商业文化，2011(4):372-373．

［13］邓杰，唐国兴．中国股票市场技术交易规则有效性的实证研究［J］．华东经济管理，2009，23(5):135-140．

［14］纪华东．中国股票市场有效性研究综述［J］．市场周刊:理论研究，2011(1):85-86．

［15］张亦春，周颖刚．中国股市弱式有效研究综述［J］．当代财经，2001(8):30-32．

Nonparametric research on the relationship between intraday movement and overnight gap of stock indices

ZHAO Zhao

(Antai School of Economics and Management，Shanghai Jiaotong University，Shanghai 200240，China)

This paper adopts the method of nonparametric statistic analysis to conduct a research on the relationship between the overnight gap and intraday movement of stock indices．The daily trading data of 7 stock markets around the world were processed and analyzed through basic statistic analysis，scattering diagram and the function figure based on R software．The analysis result shows that there is a relationship between overnight gap and intraday movement，and the relation is different with the stock market．Taking Shanghai composite index analysis data as an example，it is found that the percentage gap area as the gap and change fits better by asymptotic and Bootstrap confidence band analysis．And a profitable trading strategy based on stocks overnight gap was proposed according to the relationship between gap and change in the percentage gap interval．This also demonstrates that technical analysis is efficient to guide the stocks investment．

nonparametric statistics;stock market index;confidence band;profitable investment strategy

F830．91

A

1671-6248(2012)03-0054-06

2012-05-15

赵钊(1989-)，男，甘肃兰州人，学生。