刨花楠树高与胸径异速生长的关系
2012-01-08钟全林程栋梁苏永堃徐朝斌
胡 波,钟全林,程栋梁,苏永堃,徐朝斌
(福建师范大学a.地理科学学院;b.湿润亚热带山地生态国家重点实验室培育基地,福建福州 350007)
刨花楠树高与胸径异速生长的关系
胡 波a,b,钟全林a,b,程栋梁a,b,苏永堃a,b,徐朝斌a,b
(福建师范大学a.地理科学学院;b.湿润亚热带山地生态国家重点实验室培育基地,福建福州 350007)
通过幂指数函数的对数模型lg H=a+blgD,分析刨花楠树高H与胸径D,以及与0.25 H,0.5 H,0.75 H处直径(D)之间的关系,a和b为常数.结果表明:在刨花楠不同生长阶段其异速生长指数存在显著差异,异速生长指数随着胸径的增长而减小,而且树高与不同高度处直径之间的异速生长指数随着高度的增加而减小.植物异速生长是当前生态学研究的一个热点问题,而植物树高与胸径的关系又是异速生长研究的一个重点.本研究表明不存在一个普适的植物树高与胸径之间的关系,其指数应当随着植物的生长过程而系统减小.
树高;胸径;异速生长
近年来,随着人们对全球自然环境的认识和研究的日趋深入,人们对森林生态系统,尤其是人工林价值的认识也发生了深刻的变化,最大限度地发挥森林的生态和经济效益并对其进行准确的评估成为森林维护和管理工作者的重要任务之一,也推动了对森林生态系统的研究工作[1].目前对森林资源的研究主要是调查其树高、胸径、郁闭度、年龄、立地条件等,其中胸径、树高是最重要的两项因子,胸径与树高的关系称为树高曲线.
刨花楠(Machilus pauhoi)是一种中性偏阴树种,其多生于海拔800m以下的丘陵,它对光的要求随年龄阶段而异,幼龄期喜欢阴湿环境,生长较缓慢,中龄期喜光,生长迅速[2].它对立地条件的要求较高,喜深厚、疏松、湿润、肥沃土壤.它是一优良常绿阔叶树种,生长快,花大,外型美观,木材纹理较直,略有交织,结构较细,刨面光滑,既可用庭园绿化,又可作为用材树种,用于加工家具及室内装修.木片浸水后有粘液,可用于作化工原料具有较高的经济和观赏价值[3-4].广东、广西、福建、浙江、湖南以及江西省各地匀有分布.因此本文通过分析刨花楠树高与胸径关系,得出较能反应他们真实情况的拟合方程模型,为刨花楠的异速生长研究提供一定的理论依据.
植物的异速生长(allometric scaling)一直是人类研究的一个重点问题,植物的异速生长是描述植物个体大小和其他属性之间的非线性关系,通常以幂指数的形式表示[5-6]:

式中,y是所研究的植物某方面的属性值(如植物的生物量,体积,植物高度等),x是植物的另一个属性值,a和b为常数,b也叫异速生长指数[7].
植物的树干高度(tree height)和胸径(stem diameter)的关系,也属于植物异速生长关系的一种,因此关于树高与胸径的关系也可以用上述函数表示.对该树高与胸径异速生长关系的解释主要涉及三种模型:植物的压力自相似模型(stress selfimilarity),弹力自相似模型(elastic selfsimilarity)和几何自相似模型(geometric selfimilarity).这三种模型均来源于悬挑梁工程设计原理,它们是公认的描述树木机械设计的最佳模型[8].每种模型都在植物树干的高度、直径和质量之间假设一个单一的异速比例关系,这种关系存在于所有等级的树干之间(见表1).这三种模型是根据不同的限制因素提出的,例如,当树的机械设计符合压力相似性模型时,即植物为了最大限度地降低自上而下的风压力对植物生长的影响,树高与胸径的1/2次幂成正比(y=ax1/2)[9];弹性自相似模型认为树木为了防止由于自身质量而造成的扭曲变形,或者说树木为了保持挺拔、直立,较高的树干其树干的粗度也应该较粗,当树的机械设计符合弹性相似性模型时,树高与胸径的2/3次幂成正比(y=ax2/3)[10];当风是树的机械设计的控制因素时(即符合几何自相似性模型),树高会与胸径成正比(y=ax),这几种模型都具有大量的经验数据支持[11],但是植物的异速生长指数不是固定不变的,不同的植物之间异速生长指数不一样,同一种植物在不同的生长阶段其异速生长指数不一样,同一种植物同一生长阶段但是在不同的生长环境下其异速生长指数也是不一样的.到目前为止,已有大量研究表明树木高度与胸径之间的异速生长关系会随树木的发育而改变,在不同物种功能群中异速指数具有很大差异,因此可能不存在一个简单的、普适的植物高度和直径之间的异速关系[12].

表1 三种模型下树高(H)、胸径(D)和质量(M)之间的异速生长指数α的取值[6]Table 1 Values of the index of allometric growth(α)between height(H),diameter(D)and mass(M)in three models
在实际的应用中更多的将异速生长关系函数用对数的形式表示:

虽然方程经过对数转换之后会模糊较大数值之间的差异,同时增加较小数值之间的区别.但在处理非正态分布的数据,如种间比较等情况下,这种转换是非常有用的.因为较小的物种通常具有较大的样本数目,反之,较大的物种则具有较小的样本数目[13].
如果用H表示树高,D表示胸径,那么其表达式可以转化为lg H=a+blgD.a与b为常数,b也叫做异速生长指数,这样就可以用一次函数表示出树高的对数与胸径对数的关系.通过对植物的异速生长指数的确定,可以解释植物在生长过程中的机械设计原则.
1 研究区与研究方法
1.1 研究区概况与数据采集处理
安福县地理位置介于东经114°~114°47′,北纬27°04′~27°36′之间.地势为西北高,东南低,呈自西向东南倾斜走向,地形以低山为主,土壤以红壤、黄红壤为主,显偏酸性.成土母岩以板岩、砂岩为主,土层厚度多40~60cm,质地多团粒结构.该地区属于中亚热带季风湿润气候,其特点是气候温和,雨量充沛,日照充足,四季分明,全年平均气温17.9℃,极端低温-8.3℃,极端高温39.7℃.年平均降雨日为166d,降水量1 516.8 mm,无霜期280d.
本研究资料来源于江西省安福县标准地内242棵刨花楠大个体的树高和胸径,以及239棵刨花楠幼苗的树高和基径,刨花楠幼体的树高范围为0.08~0.40m,基径范围为0.15~0.59cm.将这些数据转化成对数形式得到树高的对数值和胸径的对数值.所选取的242株解析木,其年龄5~53a,胸径5.0~36.9cm,树高4.5~20.4m.10m以下的解析木以1m为一区分段,10m以上以2m为一区分段进行树干解析,测定解析木的带、去皮胸径,材积,各区分段的中央带、去皮直径及树高等.测出刨花楠在0.25 H,0.5 H,0.75 H处的直径,并取他们的对数值.
1.2 研究方法
首先用spss软件对处理后的数据进行线性分析.做出刨花楠大个体,幼苗的树高和胸径关系的散点图,以及0.25 H,0.5 H,0.75 H处的带皮直径的对数值的散点图(刨花楠不同树高处的树高与胸径关系中的树高是指从测量胸径处到树冠顶的距离),然后根据所得各散点图对实验数据进行模型拟合后,得到各方程的待定参数及各回归方程及其方程P值、决定系数R2.以P值评价各方程的显著水平,以决定系数R2大小评价其模型拟合程度大小,R2大说明拟合程度好,模型可靠,反之,R2小,模型则不够可靠.将得到的b值与三种模式的自相似模型的异速生长指数进行对比,判断其符合那一种模型,并比较刨花楠大个体和幼苗的异速生长指数,以及刨花楠大个体不同高处树高与直径异速生长指数的变化并分析其原因.
2 结果与分析
2.1 刨花楠大个体树高与胸径关系
根据刨花楠不同生长阶段的个体进行的分析可知,刨花楠生长的成熟阶段其用异速生长公式表示的树高与胸径关系为:lg H=0.32+0.62 lgD(图1),a=0.32,b=0.62(n=242;95%置信区间(CI):0.56~0.68;R2=0.643;P<0.001)其异速生长指数为0.62(表2).从这一阶段看,它的异速生长指数符合异速生长指数2/3的模型,即弹性自相似性模型,弹性自相似模型认为树木为了抵抗因自身质量造成的扭曲形变,或者说树木为了保持挺拔、直立的形态,较高的树干其胸径也应该较大.

图1 刨花楠大个体树高与胸径关系Fig.1 lRelationship between tree height and diameter at breast of mature Machilus

表2 刨花楠树高与胸径关系模型拟合结果Table 2 Fitting results of the model of relationship between tree height and diameter at breast of Machilus
2.2 刨花楠幼苗体树高与胸径关系
在刨花楠生长的幼体阶段异速生长公式为:lg H=-0.27+0.78lgD(图2),a=-0.27,b=0.78(n=239;0.66~0.91;R2=0.391;P<0.001),其异速指数为0.78(表2).从这一阶段看,它的异速生长指数符合异速生长指数2/3的模型,即弹性自相似性模型.在不同的生长阶段刨花楠的异速生长指数是不一样的,在幼体阶段异速生长指数为0.78,到了大个体阶段异速生长指数为0.62.很明显,异速生长指数随着胸径的增长而降低,表明了植物的异速生长率并不是不变的,它是随植物生长阶段的变化而变化的.从观察到的情况看刨花楠的异速生长指数随着树高和胸径的增长而变小,这种变化体现了刨花楠树高的增长速度与胸径的增长速度相比较是变慢了.

图2 刨花楠幼苗树高与胸径关系Fig.2 Relationship between tree height and diameter at breast of Machilus seedling
为了分析的完整性,本文分析了所有样本的胸径-树高关系.从总体的数据分析情况来看,刨花楠树高与胸径关系为:lg H=-0.15+1.03 lgD(图3),a=-0.15,b=1.03(n=481;95%的置信区间(95%CI):1.02~1.04;R2=0.980;P<0.001),其异速指数为1.03(表3),即刨花楠的树高与胸径关系符合异速生长指数为1的几何自相似模型,几何自相似模型认为风载荷是植物机械设计的控制因子,为了抵抗风力,植物投资最小的生物量在枝条的构建上,树木高度和胸径之间应成等速生长关系,即lgH=a+lgD.在表中lgH=-0.15+1.03lgD的复相关系数达到了0.980,表明了拟合方程具有很高的拟合程度.

图3 刨花楠树高与胸径关系Fig.3 Relationship between Machilus tree height and diameter at breast

表3 刨花楠不同树高处树高与直径异速生长模型拟合结果Table 3 Fitting results of allometric growth model of the tree height and the diameter at different height of
2.3 花楠树高与不同高度处直径的关系
根据散点图及拟合的结果可以得出在刨花楠的0.25 H处的直径与树高的异速生长公式为:H=0.23+0.61lgd(图4),a=0.23,b=0.61(n=242;95%的置信区间(95%CI):0.54~0.67;R2=0.597;P<0.001)故其异速生长指数为0.61(表3).符合异速生长指数为2/3的弹性自相似模型.

图4 刨花楠1/4树高处树高与树径的异速生长关系Fig.4 elationship between tree height and allometric growth of diameter of Machilus(h=1/4 H)
在0.5 H处的直径与树高的异速生长公式为:H=0.12+0.59lgD(图5),a=0.12,b=0.59(n=242;95%的置信区间(95%CI):0.53~0.65;R2=0.598;P<0.001),其异速生长指数为0.59(表3).符合异速生长指数为2/3的弹性自相似模型.

图5 刨花楠1/2树高处树高与直径异速生长关系Fig.5 Relationship between tree height and allometric growth of diameter of Machilus(h=1/2 H)
在0.75 H处的直径与树高的异速生长公式为:H=0.60+0.52lgd(图6),a=0.60,b=0.52(n=242;95%的置信区间(95%CI):0.47~0.59;R2=0.533;P<0.001),异速生长指数为0.52(表3).符合异速生长指数为1/2的压力自相似模型.
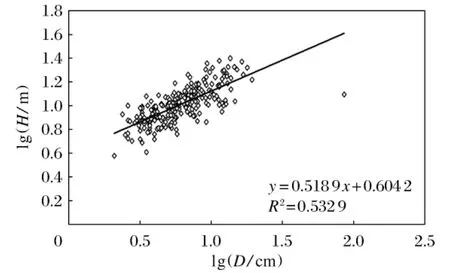
图6 刨花楠3/4树高处树高与直径异速生长关系Fig.6 Relationship between tree height and allometric growth of diameter of Machilus(h=3/4 H)
通过比较刨花楠不同高处0.25 H,0.5 H,0.75 H三处树高与直径的异速生长指数分别为0.61,0.59,0.52,很明显他们的异速生长指数在减小,越往高处其异速生长指数越小,并且从原来的符合弹性自相似模型转变到符合压力自相似模型.
3 讨 论
3.1 刨花楠树高与胸径关系
由表2可以看出,整体上刨花楠树高与胸径之间呈等速生长(即,异速生长指数为1.0),基本符合几何自相似生长模型,但是在刨花楠的不同生长阶段其异速生长指数是不同的,并且在各个阶段他们的异速指数值更接近弹性自相似模型的预测值.在刨花楠的不同生长阶段幼苗期和成熟期,前者的异速指数高于后者.这种差异主要是刨花楠胸径的增长所致.在树木发育的早期,几何自相似模型可能适合描述树高和直径的之间的异速生长关系,但到了树木发育的成熟阶段,弹性自相似模型或应力自相似模型将更适合于描述他们之间的关系.因而,没有哪个模型能够独一无二地解释所有观察到的、反映植物最优机械设计的异速生长模式,即没有统一的模型来描述所有植物的异速生长规律[14].
在刨花楠的不同生长阶段中,异速生长指数更符合弹性自相似性模型,这符合大多数学者提出的2/3模型.有学者根据大量的测量分析研究得出2/3指数模型-弹力自相似性模型是最普遍存在的一种植物机械设计模型.
在刨花楠生长的幼年阶段,由于植物个体较小,生长的环境处在林下相对阴暗潮湿,并且受到外界的干扰不大,所受到风力的影响也较小,在此阶段下的刨花楠要克服的主要是由于自身的重量所引起的影响,因此树高与胸径之间体现出弹性自相似模型的特征,其树高与胸径的异速生长率接近2/3.
到了大个体阶段,刨花楠的胸径达到一定粗度,足以抵抗一定的压力,树高能够较快的增长,树冠幅达到一定高度后使得树冠幅受到的风力大增,向下的风压也随着加大,此时刨花楠的树干生长形式的异速生长率变小,逐渐向几何自相似模型转变.
3.2 刨花楠树高与不同高度上直径的异速生长关系
通过对刨花楠解析木的树高与不同处直径关系的研究得出:它们的异速生长指数随着高度的不同而发生变化,并且它们的异速生长指数不断减小,由符合弹性自相似模型转变为符合压力自相似模型.
分析其原因:可能主要是因为在天然混交林中,幼龄阶段,刨花楠树种处于林冠下层,竞争压力大,为了能使自身生存,这时高度生长速度相对较快[15],其树高与直径的异速生长指数较大;随着年龄的增加,该树种渐渐处于林层上部,竞争压力相对较小,因此高生长速度相对较慢,异速生长指数变小.另外,在生长过程中,异速生长指数还受森林密度改变的影响.刨花楠树高与不同高度直径的异速生长关系随着高度的增长的变化,与刨花楠不同生长阶段的树高与胸径的异速生长指数变化是相符合的.
3.3 不同植物的异速生长关系
笔者参阅了国内学者的相关方面研究论文,将其幂指数方程归纳如表4.表中数据表明有些树种符合三种相似性模型,有些不符合.现将研究结果总结为以下几点:①在有些植物的不同年龄阶段它的异速生长是不同的,例如水杉在其胸径范围为7~20cm时压力相似,在其胸径为20~40cm时不符合三个模型;②有些植物的异速生长符合压力自相似模型,例如海桑树、无瓣海桑、秋茄树等;③植物的异速生长符合弹力自相似模型,例如国槐、马尾松等;④植物的异速生长符合几何自相似模型,例如赤松(药乡)、杉木(武义)等;⑤植物的异速生长与三个模型都不相符,例如海莲树、木荷、赤松(延边)等.这些不同结果的原因归结为以下几点:①植物的种类不同,在不同物种种群中异速指数具有很大差异;②植物生长阶段不同,已有大量研究表明树木高度与胸径之间的异速生长关系会随树木的生长阶段的不同而改变;③植物生长环境不同,植物异速生长的不同与植物生长密度有关,还与植物生长环境有关,比如光照、风力等因素.同时必须指出的是所研究的植物都是在野外自然环境下成长的,在室内人工调节下栽培的植物则不具备此种特性.

表4 国内学者研究异速生长模型拟合结果统计表Table 4 Statistics of the fitting results of allometric growth model studied by domestic scholars
各物种树高和胸径的比例D/H关系各不相同.然而,大多数物种符合(尽管不完全)三种机械设计模式中的一种,以前人类的大量研究表明符合弹性自相似模型的物种是最多的.弗里斯表明,在大部分植物中符合几何自相似性模型的可能会发生在个体发育的早期,而弹性或应力自相似性模型主要是树的成熟阶段.
[1]赵敏,丁慧勇.上海水杉树高与胸径关系模式分析[J].上海师范大学学报:自然科学版,2009,38(5):531-535.
[2]陈国彪.刨花楠的利用与培育技术[J].广西林业科学,2004,33(4):212-213.
[3]钟全林,胡松竹,黄志强,等.刨花楠生长特性及其生态因子影响分析[J].林业科学,2002,38(2):165-168.
[4]钟全林,张振碱,张春华,等.刨花楠生物量及其结构动态分析[J].江西农业大学学报[J].2001,23(4):533-536.
[5]Peters R H.The Ecological Implications of Body Size[M].Cambridge:Cambridge University Press,1983:197-198.
[6]Niklas K J.Size-dependent variations in plant growth rates and the“3/4-power rule”[J].American Journal of Botany,1994,81:134-144.
[7]韩文轩,方精云.幂指数异速生长机制模型综述[J].植物生态学报,2008,32(4):951-960.
[8]Niklas K J.Size-dependent Allometry of Tree Height,Diameter and Trunk-taper[J].Annals of Botany,1995,75:217-227.
[9]Mc Mahon T A,Kronauer R E.Tree structures:deducing the principle of mechanical design[J].Journal of Theoretical Biology.1976,59:443-466.
[10]MeMahon T A.Size and shape in biology[J].Science,1973,179:1201-1204.
[11]King D,Loucks O L.The theory of tree bole and branch fom[J].Radiation and Environmental Biophysics,1978,15:141-172.
[12]Girnish T J.Adaptation to sun vs.shade:a whole-plant perspective[M]∥Osmund CD,Hall DB,van Caemmerer S,eds.Ecology of photosynthesis in sun and shade. Cambridge:Cambridge University Press,1973:63-92.
[13]程栋梁.异速生长关系在生物学中的应用[J].沈阳大学学报,2009,21(6):12-15.
[14]Niklas K J.The scaling of plant height:a comparison among major plant Glades and anatomical grades[J].Annnls of Botany,1993,72:165-172.
[15]钟全林,黄志强,胡松竹,等.刨花楠干形结构分析[J].江西农业大学学报,2002,24(2):232-236.
[16]王佳燕,余雪标,周光益,等.海南东寨港主要红树植物树高与胸径相关关系[J].中国农学通报,2007,23(9):564-568.
[17]郑小贤,刘东兰.基于柱体屈曲理论的树高曲线式和材积式[J].北京林业大学学报,1997,19(1):89-92.
[18]刘敏,张日升,徐贵军,等.辽宁樟子松人工林树木胸径与树高、材积的相关关系[J].防护林科技,2010(1):36-37,41.
[19]高祥斌,刑柱东.聊城市主要行道树国槐胸径与树高关系研究[J].北方园艺,2010(10):128-130.
[20]吕勇.林木树高曲线模型研究[J].中南林学院学报,1997,17(4):86-89.
[21]王利,丰震,白世红,等.麻栎树高与胸径相关关系的研究[J].山东林业科技,2005(4):33-34.
[22]刘敬灶.木荷人工林相对树高曲线模型的研究[J].林业勘察设计,2008(1):18-20.
[23]刘安兴.树高曲线聚类分析研究[J].浙江林学院学报,2001,18(3):228-232.
[24]徐悦,陈昌华,蒋之富,等.天然赤松胸径与树高相关模型的研究[J].林业调查规划,2008,33(3):56-58.
[25]谢哲根,刘安兴,陈学,等.相对树高曲线研究[J].浙江林学院学报,1998,15(1):69-75.
[26]蒋艳,李任波,李玻.云南松树高——胸径生长关系模型[J].内蒙古林业调查没汁,2010,33(1):57-59.
[27]陈新美,张会儒.柞树林树高结构的研究[J].西北林学院学报,2010,25(4):130-134.
[28]王利,李建华,乔勇进,等.药乡林场赤松树高与胸径相关关系的研究[J].山东林业科技,2002(1):9-10.
[29]蒋钦斌.杉松人工林伐区调查设计中树高曲线图的绘制与应用[J].福建林业科技,2007,34(2):72-74,88.
[30]陈建珍,李任波,潘涌智,等.基于Matlab的树高曲线拟合试验及评价[J].林业调查规划,2007,32(3):1-3.
Relationship between Machilus’Height and Allometric Growth of Diameter at Breast
HU Boa,b,ZHONG Quanlinga,b,CHENG Donglianga,b,SU Yongkuna,b,XU Chaobina,b
(a.School of Geography Science;b.State Key Laboratory Breeding Base of Humid Subtropical Mountain Ecology,Fujian Normal University,Fuzhou 350007,China)
The relationships between Machilus'height(H)and diameter at breast(D),and the diameter(D)at 0.25 H,0.5 H,and 0.75 H,are analyzed by logarithmic model of power exponent function:lg H=a+blgD.The results show that,there are significant differences in the index of allometric growth in different growth stages of Machilus.The index of allometric growth between the tree height and the diameter at different height decreases with the growth of the diameter at breast;and decreases with the increase of height of the tree.It is indicated that,there is not a universal relationship between tree height and diameter at breast,the index should be systematically reduced with the growth of plant.
tree height;diameter;allometric growth
Q 94
A
1008-9225(2012)03-0009-06
2012-02-09
国家自然科学基金资助项目(30901151,31170374,31170596);国家农业科技成果转化资金项目(2011GB2C400005);福建省科技厅重点项目(201010004)联合资助.
胡 波(1987-),男,江西萍乡人,福建师范大学硕士研究生;钟全林(1965-),男,江西抚州人,福建师范大学教授,博士,硕士生导师.
王 颖】
