线性矩阵方程的广对称解＊

秦晓伟，刘新国

（中国海洋大学数学科学学院，山东青岛266100）

线性矩阵方程的广对称解＊

秦晓伟，刘新国

（中国海洋大学数学科学学院，山东青岛266100）

研究线性矩阵方程的广对称解，对Bunch，Sun，Tisseur等人的一些已有结果进行推广，并把所得结果用于结构向后误差分析。

线性矩阵方程；广对称矩阵；结构矩阵

线性矩阵方程具有广泛的应用，例如不变子空间的扰动分析［1］、特征空间的向后误差分析［1－2］、特征值反问题、结构向后误差分析［2］、多元统计分析［3］、有限元模型修正［4］等。

已经有大量的关于线性矩阵方程的研究，XB＝C是最简单同时也是最常见的矩阵方程。针对这个矩阵方程，Sun［1］推广Bunch，Demmel，Van Loan［5］的结果，给出了对称（Hermite）解及最小F范数解的显示表达式，并应用于研究特征子空间的结构向后误差。Tisseur［2］把Sun的结果推广到反对称（反Hermite）矩阵，并用于研究结构向后误差分析。

本文研究线性矩阵方程的广对称解。使用Karow，Kressner和Tisseur［6］的纯量积框架定义了广对称矩阵。讨论了线性矩阵方程XB＝C的广对称解，所得结果是Sun及Tisseur有关结果的推广。研究一般的线性矩阵方程的广对称解，所得结果在有限元模型修正方法中有潜在应用。

本文中，K表示实数域R或复数域C，相应地，Km×n表示Rm×n或Cm×n。并用＊表示矩阵转置T（实情形）或共轭转置H（复情形），其他记号是常规的，可参见文献［7］。

1 广对称矩阵

定义1 给定β∈K满足｜β｜＝1，以及P∈Kn×n满足P2＝In，P＊＝P。一个矩阵A∈Kn×n若满足

则称矩阵A为广对称矩阵。

以上定义的广对称矩阵类包含了一些特殊的重要子类，例如：

（1）K＝R，此时β＝±1，P是非奇异正交阵。取P＝In，则得到实对称矩阵类及反对称矩阵类。取P＝［en，…，e1］，这里［e1，…，en］＝In，则得到（关于斜对角线对称的）斜对称矩阵类及斜反对称矩阵类［7］。

（2）K＝C，取β＝±1，P＝In，则分别得到Hermite矩阵类及反Hermite矩阵类。

在Kn上引入纯量积［6］

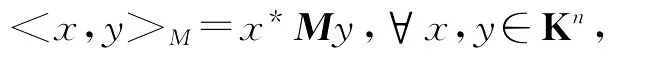
这里M∈Kn×n是某个给定的非奇异矩阵。对于A∈Kn×n，依上述纯量积可以引入A的伴随矩阵A☆如下：

易知

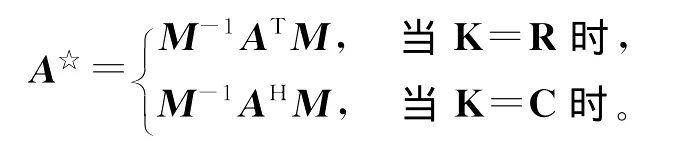
如果A☆＝A，则称A是自伴矩阵；如果A☆＝－A，则称A是反自伴矩阵。Kn×n中全体自伴矩阵构成的集合J为一个Jordan代数；全体反自伴矩阵构成的集合L为一个Lie代数。更详细的讨论见文献［6］。从应用看，一类重要的纯量积＜，＞M为酉对称和正交对称的（unitary and orthosymmetric）情形：M为酉阵，且存在β0∈K，｜β0｜＝1，使得

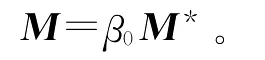
此时，M2＝β0In。因此M的特征值为。由于M为酉阵，因此，存在酉阵Q使得

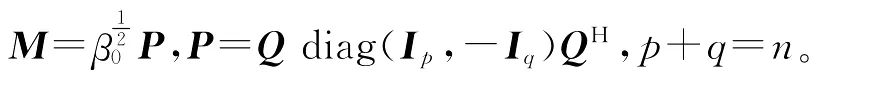
此时对于自伴矩阵A，有

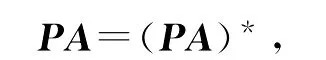
对于反自伴矩阵A，有

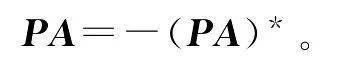
因此，定义1引入的广对称矩阵包含了这2类矩阵。

引理1 对于A∈Kn×n，

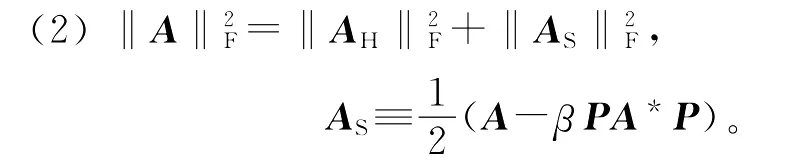
又由于

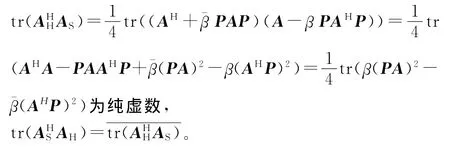
从而

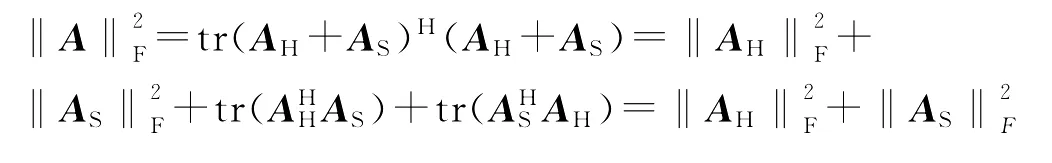
2 矩阵方程XB＝C的广对称解

给定B，C∈Kn×p，考虑线性矩阵方程

令Y＝PX，则方程（2）等价于下述方程

易看出，X是（2）的广对称解的充分必要条件是Y是（3）的解，且

定理1 方程（3）有满足（4）的解的充要条件为

这里PBH＝B＋B。

当（5）满足时，方程（3）满足（4）的解的一般形式为

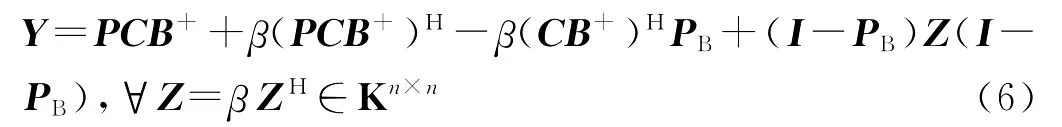
其中，最小F范数解为

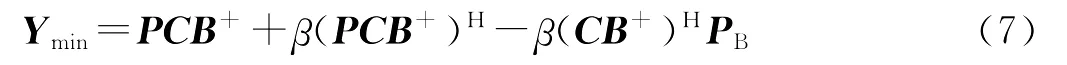
证 设B的奇异值分解为

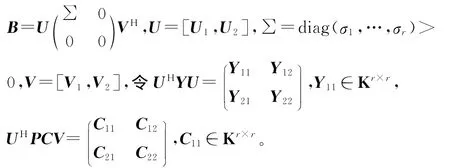
那么方程（3）等价于

易知，（8c）等价于CPBH＝C。令

那么，（3）有满足（4）的解的充要条件为

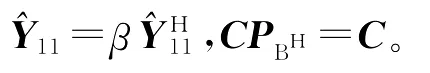
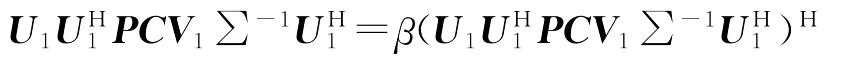
即

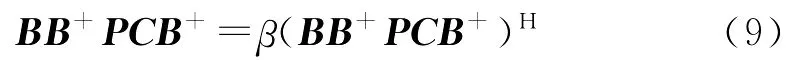
而（9）等价于

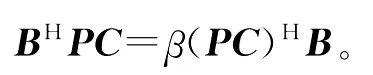
从而，（3）有满足（4）的解的充要条件为（5）。

当（5）满足时，满足（4）的解的一般形式为

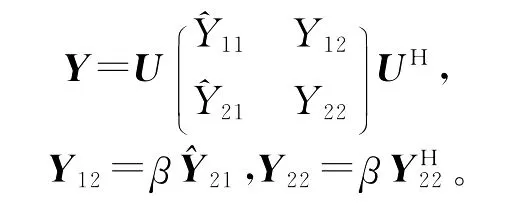
由定理1及Y＝PZ，P－1＝P，直接得出下述结论。

定理2

（1）方程（2）有广对称解的充要条件为

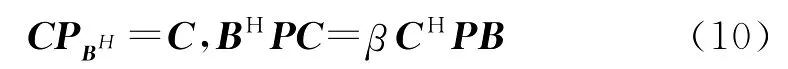
（2）当（10）满足时，（2）的广对称解的一般形式为

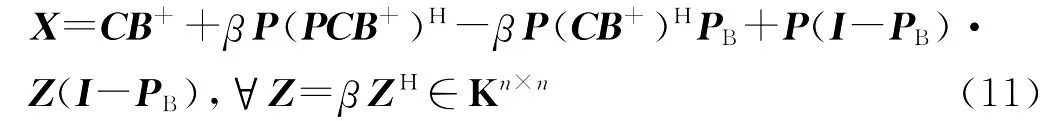
其中最小范数解为

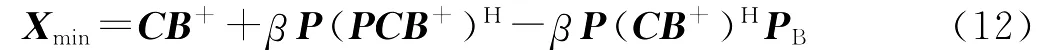
注：取K＝R，则定理2得到Bunch，Demmel和Van Loan［5］的结果。取K＝C，β＝1，得到文献［1］中的引理1.4。取K＝C，β＝－1，得到文献［2］中的引理2.6。

3 一般线性矩阵方程的广对称解

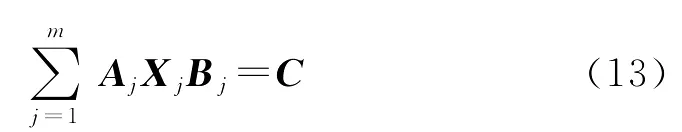
考虑与（13）关联的矩阵方程组：

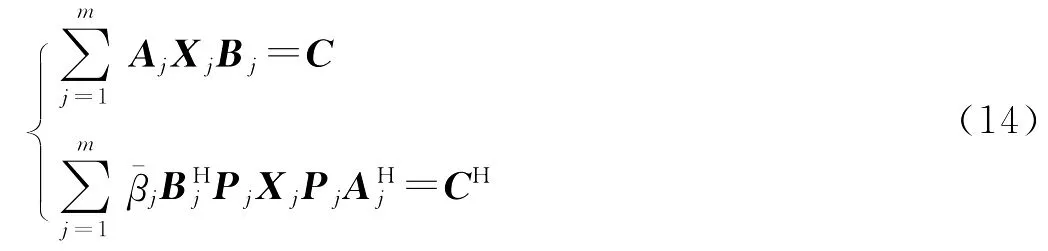
定理3

（1）方程（13）的广对称解必是（14）的解。

（2）若（X1，…，Xm）为（14）的解，则其广对称化

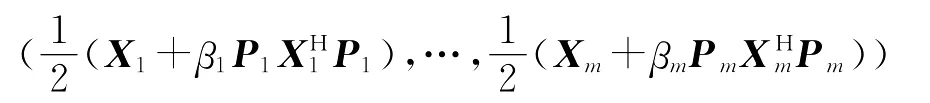
也是（14）的解。

（3）方程组（14）的最小F范数解必是广对称的。

证 直接检验即知结论（1）成立。为证明结论（2），先证

由于（X1，…，Xm）为（14）的解，故有

两式相加，有

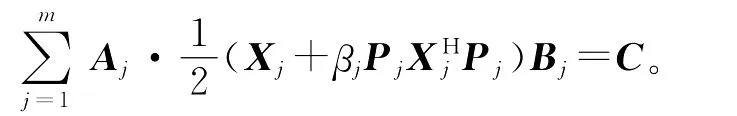
而由

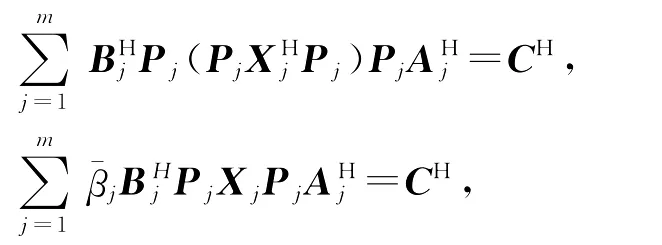
两式相加，得

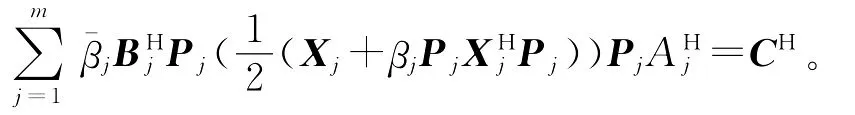
故结论（2）得证。

若（X1，…，Xm）为（14）的最小F范数解，由引理1，有

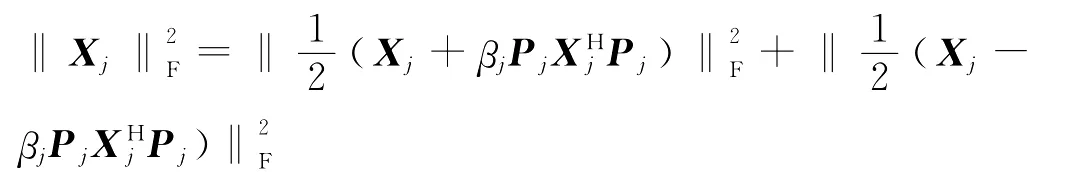
又由结论（2），可知必有

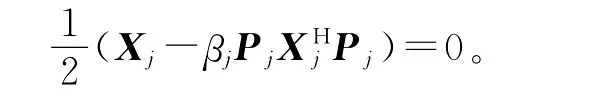
推论1 方程（13）有广对称解的充分必要条件为（14）有解。

命题1 若（14）有解，则其解集合为闭凸集。

定理3及推论1表明，如果（14）有解，则必有最小F范数解，且最小F范数解也是（13）的最小F范数广对称解。这样，就把求（13）的最小F范数广对称解转化为求（14）的最小F范数解。记

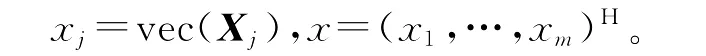
使用拉直运算，（14）改写为

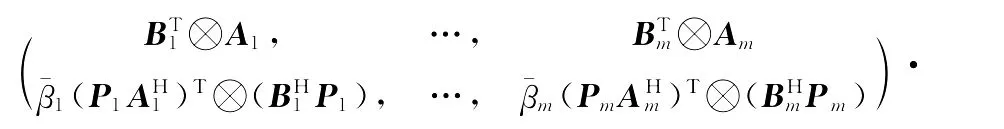
由此可以得到（15）的最小2范数解

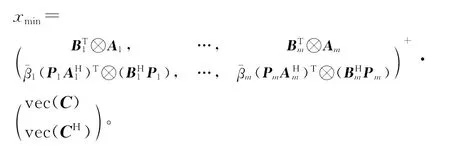
然后，用vec的逆运算，由xmin可以得到（13）的最小F范数广对称解。

以上结果在二次特征值问题的结构向后误差分析［2］中有用，下面对此简要说明。考虑二次特征值问题

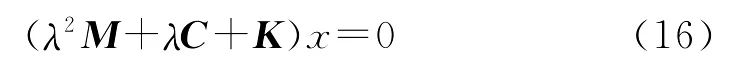
如果数λ及非零向量x满足（16），则称λ为二次矩阵多项式Q（λ）≡λ2M＋λC＋K的一个特征值，x叫对应的特征向量。在震动分析中，一类重要的二次矩阵多项式Q（λ）满足Hermite性：

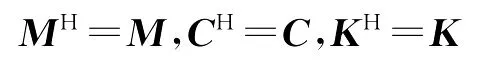
而在旋转系统研究中出现的二次矩阵多项式Q（λ）满足：

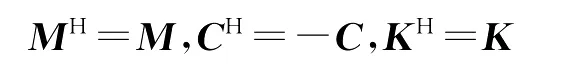
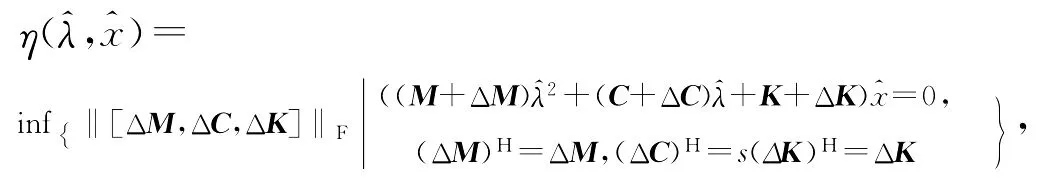
这里s＝±1。

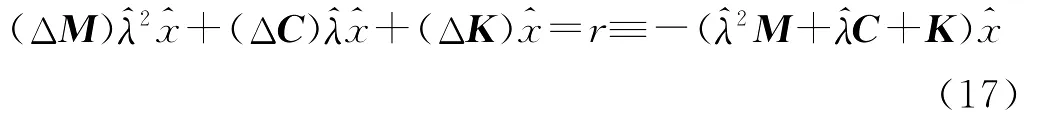
这是方程（13）的特殊情形。令Q0为酉阵，使得为单位阵In的首列，并令

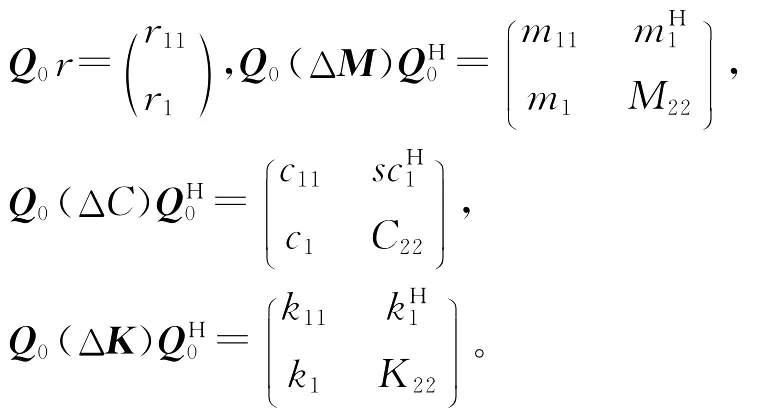
则（17）等价于

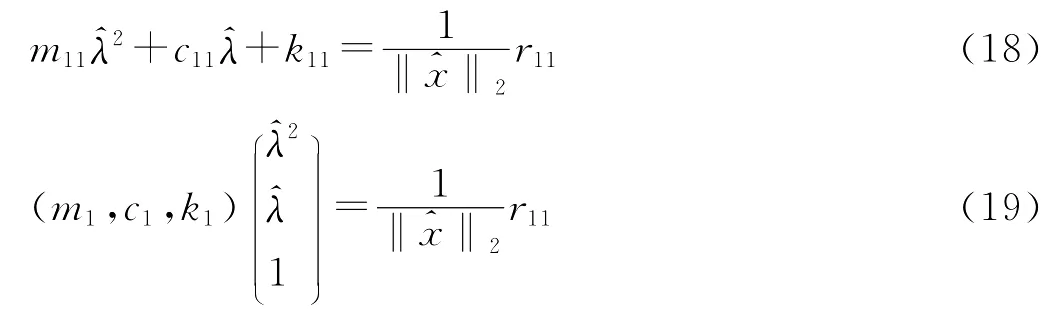
由文献［2］中引理1.3，（19）的最小F范数解为

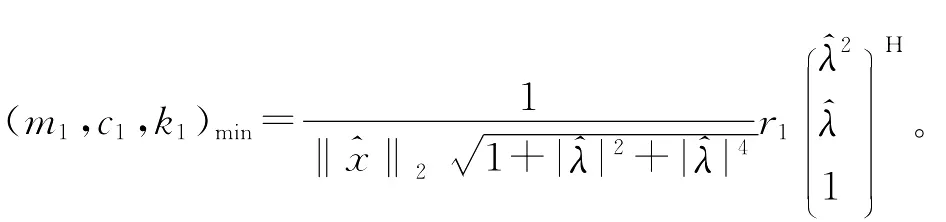
而（18）的最小F范数广对称解由

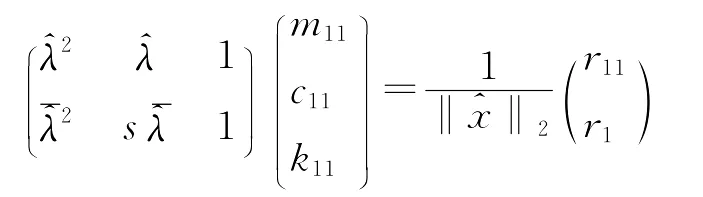
的最小2范数解确定。

［1］ Sun J G.Backward perturbation analysis of certain characteristic subspace［J］.Numer Math，1993，65：357－382.

［2］ Tisseur F.A chart of backward errors for singly and doubly struc－tured eigenvalue problems［J］.SIAM J Matrix Anal Appl，2003，24：877－897.

［3］ Penrose R.On best approximate solutions of linear matrix equations［J］.Proc Cambridge Philos Soc，1956，52：17－19.

［4］ Qian J，Xu S F，Bai F S.Symmetric low－rank corrections to quadratic models［J］.Numer Lin Alg Appl，2009，16：397－403.

［5］ Bunch J R，Demmel J W，Van loan C F.The strong stability of algorithms for solving symmetric linear systems［J］.SIAM J Matrix Anal Appl，1989，10：494－499.

［6］ Karow M，Kressner D，Tisseur F.Structured eigenvalue condition numbers［J］.SIAM J Matrix Anal Appl，2006，28（4）：1052－1068.

［7］ 孙继广.矩阵扰动分析［M］.第二版.北京：科学出版社，2001.

［8］ Recht B，Fazel M，Parrilo P.Guaranteed minimum－rank solutions of linear matrix equations via nuclear norm minimization［J］.SIAM Review，2010，52（3）：471－501.

Generalized Symmetric Solutions of Linear Matrix Equations

QIN Xiao－Wei，LIU Xin－Guo
（School of Mathematical Sciences，Ocean University of China，Qingdao 266100，China）

This paper deals with generalized symmetric solutions of linear matrix equations.Some wellknown results proved by Bunch，Sun，and Tisseur are extended.The results obtained are useful in structured backward error analysis.

linear matrix equation；generalized symmetric matrix；structured matrix

O241.6

A

1672－5174（2012）1－2－173－04

山东省自然科学基金项目（Y2008A07）资助

2011－03－01；

2011－05－09

秦晓伟（1987－），女，硕士生。E－mail：qinxiaowei198782＠163.com

AMS Subject Classification：15A24

责任编辑 朱宝象