基于云模型的不确定性变量半定量化研究
2012-01-07王洪利
王洪利
(西安交通大学 管理学院,西安710004)
0 引言
现实中需要处理的复杂系统问题往往都是定性的、难以量化的,为了弥补定量方法的缺陷,钱学森先生提出了定性与定量相互融合的综合集成方法及其理论体系,综合集成方法的实质就是将专家群体、知识体系、数据与信息体系和计算机体系结合起来,从定性到定量进行综合集成,实现以人的思维、思维成果、人的知识、智慧为主以及各种情报、数据信息集成起来的大成智慧的综合集成[1]。综合集成法为处理难以量化的复杂系统问题提供了理论指导。管理科学的研究对象中包括大量的由无数个体组合而成的无限多样性和复杂性的复杂系统,采用建模仿真的手段来研究复杂系统内在运行机制是复杂系统研究的最主要方法。定性仿真是以定性建模和定性推理为基础的,定性建模理论研究如何建立不完备知识系统的模型,即定性模型。定性推理则是研究如何用这种定性知识模型进行形式化推理,把定性推理应用于系统定性模型上,通过推理来产生和解释系统的行为便是定性仿真。由于系统的复杂性和参数的难以量化,系统过于复杂和知识的不完备[2],复杂系统研究主要采用的是定性仿真。但复杂系统仿真的发展趋势是采用定性定量相融合的仿真,也被称为半定性半定量仿真,微观上分为在定性仿真中使用定量信息的仿真和在定量仿真中使用定性信息的仿真两种[3],复杂系统的特点决定其仿真应以前一种为主。但在当前复杂系统的量性融合仿真中,仿真的可靠性不高,定性与定量相互脱节,不能同时为系统建模和仿真利用。产生这种情况的主要原因在于:复杂系统仿真中,定量信息没有进行有效的定性表示;定性信息和定量信息相互不能有效转化。解决以上问题的关键就是从仿真系统中变量表示这个最根本的基石入手,引入更加有效的定量信息定性表达模型和定性信息与定量信息的互相转化方法。并在此变量表达模型的基础上,研究具有量性融合特征的半定性仿真的定性建模、定性推理的理论和方法。
已有的研究中,为了解决系统仿真中不确定变量的半定量化的问题,提出以下有代表性的不确定性变量的定量化方法:(1)基于区间数的方法[4];(2)模糊数方法[5];(3)概念灰数方法[6]。
参考和借鉴钱学森先生的综合集成思想和方法,本文将在系统仿真中,引入擅长量性转化的云模型作为复杂系统中不确定性变量的表示方法,对复杂系统仿真中不确定性变量的半定量化方法进行分析和研究。
1 云模型及其基本概念
云模型是由中国的著名学者李德毅院士1995年提出的一种定性表达与定量互相转化的模型[7]。从其诞生至今在解决诸如世界著名难题三维倒立摆控制、知识发现与数据挖掘、评价与决策、信息与控制等诸多方面和领域取得了较大的成功应用。
云和云滴[8]:设U是一个用数值表示的定量论域,C是U上的定性概念,若定量值x∈U是定性概念C的一次随机实现,x对C的确定度μ(x)∈[0,1]是有稳定倾向的随机数:μ:U→[0,1] ∀x∈Ux→μ(x),则x在论域U上的分布称为云(Cloud),记为云C(X).每一个x称为一个云滴。如果概念对应的论域是n维空间,那么可以拓广至n维云。
云模型所表达概念的整体特性可以用云的数字特征来反映。云用期望Ex(Expected value)、熵En(Entropy)和超熵He(Hyper entropy)这3个数字特征来整体表征一个概念,多维云模型的整体特征可由多组数字特征表示,期望Ex是云滴在论域空间分布的期望,是最能够代表定性概念的点,或者说是这个概念量化的最典型样本;熵En代表定性概念的可度量粒度,熵越大通常概念越宏观,也是定性概念不确定性的度量,由概念的随机性和模糊性共同决定。一方面En是定性概念随机性的度量,反映了能够代表这个定性概念的云滴的离散程度;另一方面又是定性概念亦此亦彼性的度量,反映了在论域空间可被概念接受的云滴的取值范围;超熵He(Hyper entropy)是熵的不确定性度量,即熵的熵,由熵的随机性和模糊性共同决定。用三个数字特征表示的定性概念的整体特征记做C(Ex,En,He)。
一维正态云模型[9][10]:ArForward(C(Ex,En,He))是一个把定性概念的整体特征变换为定量表示的映射π:C→∏,满足以下条件:
(1)Θ={ti|Norm(En,He)的一次实现i=1..N}
(2)X={xi|xi为Norm(Ex,ti)的一次实现ti∈Θ,i=1..N}
其中,Norm(μ,δ)为期望为μ方差为δ的正态随机变量,N为云滴的个数。
利用正态云,就可以把定性概念C(Ex,En,He)变换为数值表示的云滴集合,实现了概念空间到数值空间的转换。一维正态云可以拓广至n维正态云。其中正态云模型是最重要的一种云模型,李德毅院士已证明了正态云模型的普适性[9]。
2 基于云模型的不确定性变量的半定量化
首先,需要明确一下不确定性变量和定性变量的区别。定性变量是不用数值型来体现的一组变量。比如性别、宗教信仰、客户满意度等等。定性变量表示的并非真有数量上的变化,而只有性质上的差异。这些量还可以分为两种,一种是有序变量,它没有数量关系,只有次序关系,如某教师的工作评价分为优秀、良好、一般等;另一种是名义变量,这种变量既无等级关系,也无数量关系,如颜色(红、黑)、性别(男、女)等。定量变量是可用具体数值来表示的变量,就是通常所说的连续量,如产量、库存、现金、发表论文的数量等,它们是由测量或计数、统计所得到的量,这些变量具有数值特征,称为定量变量。确定性变量是指根据现有的客观条件和人们头脑中的知识和经验可以确定其具体值(定性或定量值)的变量。不确定性变量是指由于系统的复杂性,根据现有的客观条件和人们头脑中的知识和经验无法确定其具体数值,但通过人们的观察、判断和分析可以判断其大致范围的变量。从以上可以看出,不确定性变量可能是定量变量,也可能是定性变量。不确定变量在我们处理复杂系统问题时是普遍存在的一种变量。不确定性变量不是我们对其一无所知的变量,也不是完全透彻清楚了解其具体取值的变量。除此之外,某些定性变量具有“与生俱来”客观的不确定性存在。如对人按年龄划分分为少年、青年、中年、老年等几个阶段,那么一个人16岁,属于少年还是青年呢?人们总是回答属于青年的可能性是多少,同时也没有否定有属于少年的可能性。这种定性划分上中间临界值就客观上存在很大的不确定性。
对于以上描述的不确定性变量的取值的获取,一直是各相关领域研究的关键和难点问题。在复杂系统的仿真中,本文对不确定性变量取值的获取,采取在社会科学和管理科学中的德尔菲、调查、访问、头脑风暴法等科学实用的方法来获取专家的判断。
假设对象集合为O={o1,o2,...,on},对象O的定性变量 集合 为X={x1,x2,...,xn},专 家集 合为E={e1,e2,...,en}。以下分为几种情况来研究群体领域专家的判断值转化为半定量的云模型表示的方法:
(1)假如不同专家给出的判断值是不同的准确值(不是区间)
表1为第k个专家ek对各对象变量的判断值。其中表示第k个专家对j个对象的第i个变量的判断值。
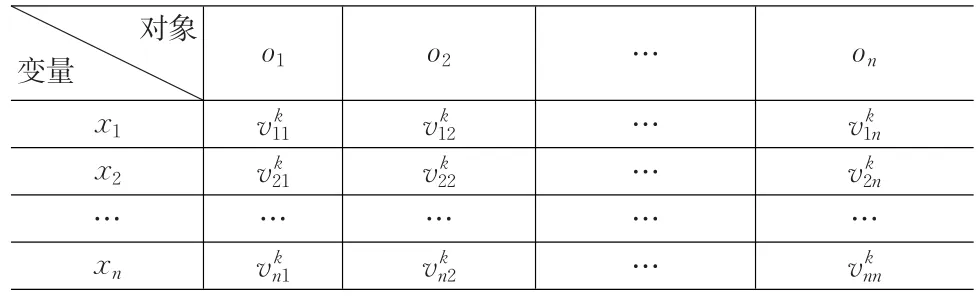
表1 第k个专家ek对各对象变量的判断值
根据表1的数据首先针对单个对象oj的变量xi统计各取值的专家频次(表2)。

表2 对象oj的变量xi的各取值频次统计

表3 变量xi的各取值的专家个数的比例
表3中所给的pi就是该变量取vi的可能性,越多的专家选择此选项,则表示不确定性变量取该值的可能性越大。将pi最大时的vi的取值记为vmax(pi)。
如果表2中vi的个数足够多(即个数多到数据分布符合正态分布规律特征),首先将表2绘制成直方图(横坐标为vi,纵坐标为取该值的专家的个数),采用云模型理论中的方法,创建该不确定性变量取值的云模型。步骤如下:
①根据“复杂问题相信和依靠领域专家”与“少数服从多数”两个基本准则,取群体专家判断所对应的云模型的数字特征中的期望Ex=vmax(pi)。如果存在两个以上的相等的pi,则在一定的水平阈值δ内,选取其中最左边和最右边的两个vi,作为梯形云的左期望和右期望(只有一个pi最大,可看成左期望等于右期望)。
②分别从左期望向左和右期望向右,将熵值从0以较小的步长逐渐增加,直到左右半正态云的函数值与直方图值之差小于误差容许阈值。将左右两个半正态云的熵值记为梯形云的两个熵值Enl、Enr。
可将以上两步过程看成将整个数据集只变换成一个云模型的云变换过程。
④各根据下式计算左右半正态云模型的超熵:
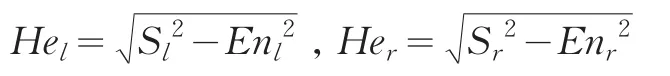
如果表2中vi取值的数量不是足够多,但多于两个,为了最好的拟合数据可使用最小二乘法,计算云的数字特征。如果表2中vi取值的数量少到只有两个。则可以采用几何云的方法来计算云的数字特征[10]。
(2)考虑到大多数专家对某个定性变量量化赋值可能许多不确定性,而且还涉及到个人判断因素,通常很难甚至不能确定地说出是多少,但总能说出“大约是多少”或“在多少到多少之间”,即给出不确定性变量量化的区间值。为此作如下定义:
定义1 设区间有两个区间[a,b],[c,d],如果a<c,b<d,则称区间[a,b]<[c,d]。如果a<c,则称区间[a,b]“左小于”区间[c,d]。如果d>b,则称区间[c,d]“右大于”区间[a,b]。
定义2 如果存在一个实数点x∈[a,b],则称x“点包含于”区间[a,b]。

表4 序列中点包含vi的区间个数

表4 序列中点包含vi的区间个数
取值vi序列中点包含vi的区间个数q′i v1 vk v2 q′1 q′2……q′k

表5 序列中点包含vi的区间个数占全体包含总数的比例
首先将表4绘制成直方图(横坐标为vi,纵坐标为序列中点包含vi的区间个数),采用云模型理论中的方法,创建该不确定性变量取值的云模型。步骤如下:
①根据表5取群体专家判断所对应的云模型的数字特征中的期望。如果存在两个以上的相等的,则在一定的水平阈值δ内,选取其中最左边和最右边的两个vi,作为梯形云的左期望和右期望(只有一个最大,可看成左期望等于右期望)。
②分别从左期望向左和右期望向右,将熵值从0以较小的步长逐渐增加,直到左右半正态云的函数值与直方图值之差小于误差容许阈值。将左右两个半正态云的熵值记为梯形云的两个熵值Enl、Enr。
可将以上两步过程看成将整个数据集只变换成一个云模型的云变换过程。
④各根据下式计算左右半正态云模型的超熵:
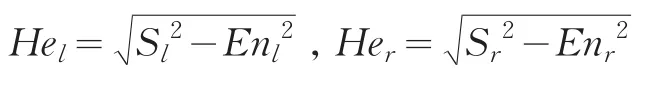
3 结论
本文提出了面向复杂系统定性仿真,从理论和方法上提出了一种基于云模型的不确定性变量的半定量化方法。该方法将充分发挥云模型在定性变量半定量化表示、量性融合与转化方面的优势,为复杂系统中不确定性变量的半定量化提供一种可供借鉴的方法,将可能促进定性与定量仿真的进一步融合。进一步的研究工作包括在应用中验证本文所提出的方法等。
[1]顾基发,王浣尘,唐锡晋.综合集成方法体系与系统学研究[M].北京:科学出版社,2007,(1).
[2]胡斌,肖人彬.复杂系统的定性仿真[J].系统仿真技术,2006,2(1).
[3]陈宗海,段家庆,桂旺盛.智能模拟之定性定量仿真的发展[J].自动化博览,2005,(s1).
[4]Benjamin Kuipers,Daniel Berleant.Using Incomplete Quantitative Knowledge in Qualitative Reasoning[C].AAAI Press.The Seventh Conference on Artificial Intelligent,1988.
[5]Qiang Shen,Roy Leitch.Extending Qualitative Simulation by the Use of Fuzzy Sets[J].IEEE Transaction on Systems,Man,and Cybernetics,1992,22(2).
[6]黄元亮.灰色定性仿真基础研究[D].中国科学技术大学,博士学位论文,2004.
[7]李德毅,孟海军,史雪梅.隶属云和隶属云发生器[J].计算机研究和发展,1995,32(6).
[8]邸凯昌.空间数据发掘与知识发现[M].武汉:武汉大学出版社,2001.
[9]李德毅,刘常昱.论正态云模型的普适性[J].中国工程科学,2004,6(8).
[10]张勇,赵东宁,李德毅.相似云及其度量分析方法[J].信息与控制,2004,33(2).
