线性回归方法在数据挖掘中的应用和改进
2012-01-07邵鸿翔
邵鸿翔
(洛阳理工学院 工程实训中心,河南 洛阳 471023)
0 引言
线性回归是一种古老类型的技术统计,是重要的也是最有用的挖掘工具之一。线性回归能够使挖掘者找到数据中最有价值和最深入的发现,同时,也很容易解释在被发现的关系上发生了什么。
本质上,线性回归是一种探索式、验证性的方式,寻找穿过状态空间的单独一条直线以便使这条直线尽可能地靠近空间中的所有点。当状态空间多于二维时,它不是恰好一条直线。在三维空间中,它是一个面,在多维空间中,它将是二维空间中直线的高纬度模拟。
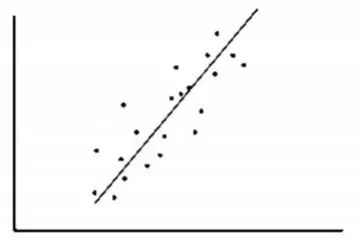
图1 典型的二维线性回归
以二维的状态空间为例,只要数据很好地聚合至少大致接近于一条直线(如图1所示),就可以对数据集合进行解释和预测。因为直线被调整得离所有的点尽可能近,当通过一个已知变量进行预测时,其预测值在状态空间中应当在直线附近。所以,直线上的点所返回的变量值是一个合理值的近似估计值。
1 传统线性回归模型
1.1 一元线性回归模型
在线性回归中,最简单的模型就是一元线性回归。我们对于x取定一组不完全相同的值x1,x2,…,xn,设Y1,Y2,…,Yn分别是在x1,x2,…,xn处对Y的独立观察结果,称(x1,Y1),(x2,Y2),…,(xn,Yn)是一个样本,对应的样本值记为(x1,y1),(x2,y2),…,(xn,yn)。其总体模型可以表示为:

其中,εi是“噪声”变量,是均值为0,标准差为σ的正态分布随机变量。设b0和b1是对β0和β1的估计,由统计学知识不难得出,在xi处对Y的回归估计为:

残差(误差)为:

根据最小二乘法可知,最好的回归直线是选择b0和b1使得总的误差(残差平方和SSR)最小:
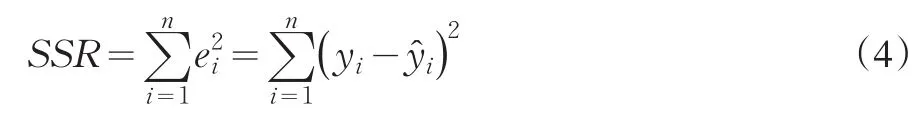
由极值原理可解得:
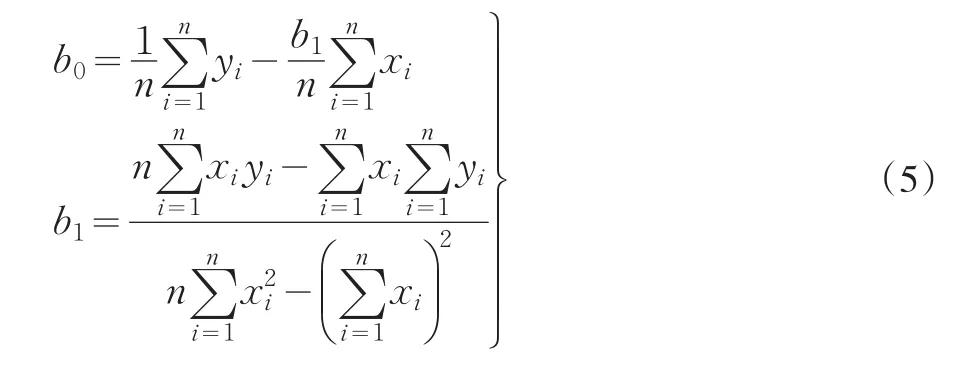
1.2 可转化为线性回归的曲线回归模型
在实际中,常会遇到更为复杂的回归问题,而不仅仅是简单的一元线性回归,但在某些情况下,可以通过适当的变量转换,将其化为一元线性回归来处理。
以下是几种常见的可转化为一元线性回归的模型(其中α,β,σ2是与x无关的未知参数):
将原式两边取对数得:

令 lnY=Y′,lnα=a,β=b,x=x′,lnε=ε′,可转化为一元线性模型:
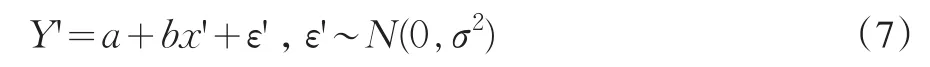
(2)Y=αxβ⋅ε,lnε~N(0,σ2)
将原式两边取对数得:

令lnY=Y′,lnα=a,β=b,lnx=x′,lnε=ε′,可转化为一元线性模型:
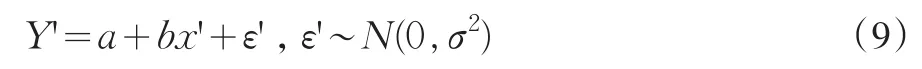
(3)Y=α+βh(x)+ε,ε~N(0,σ2),h(x)是x的已知函数
令α=a,β=b,h(x)=x′,可转化为一元线性模型:
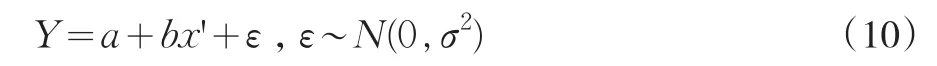
1.3 多元线性回归模型
与一元线性回归模型类似,假设自变量为x1,x2,…,xp(p>1),对应的样本值记为 (x11,x21,…,xp1,y1),(x12,x22,…,xp2,y2),…,(x1n,x2n,…,xpn,yn)。则多元线性回归模型可表示为:
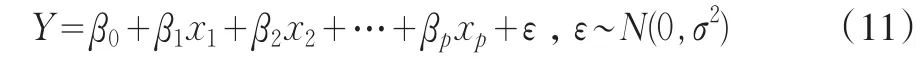
设b0,b1,…,bp是对β0,β1,…,βp的估计,则在xi处对Y的回归估计为:
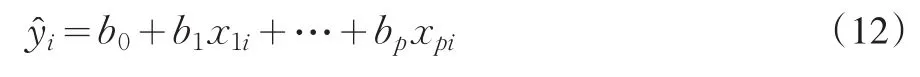
根据最小二乘法和极值原理可得:
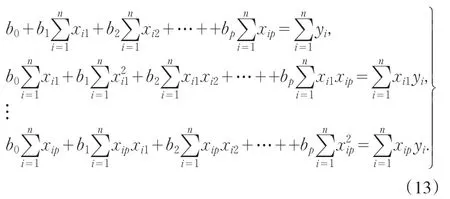
式(13)称为正规方程组,为了求解的方便,可将式写成矩阵的形式,为此,引入矩阵:
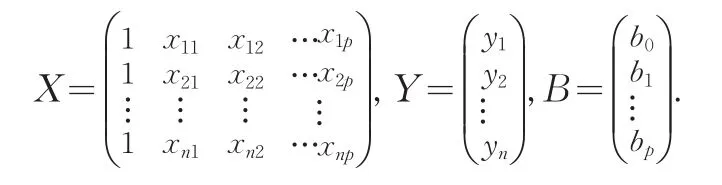
于是式(13)可以写成:

其中,XT为X的转置矩阵。假设(XTX)-1存在,可得:
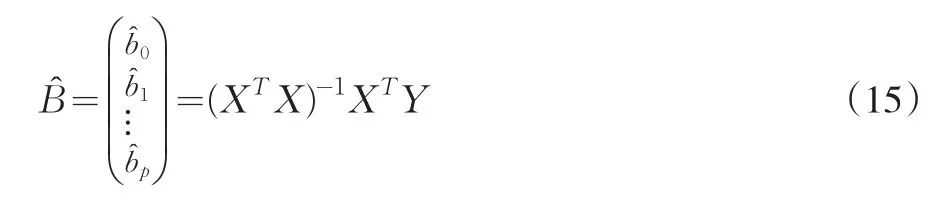
即可得回归方程:
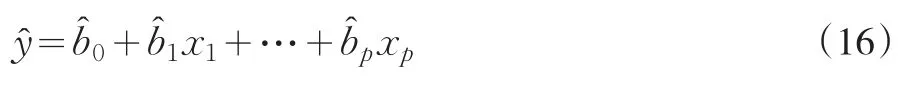
2 线性回归在数据挖掘中的应用
由于线性回归是一种常用的统计技术,并且被普遍的适用于许多领域,因此提供线性回归功能的工具有很多。专业的统计软件SPSS和SAS,数学软件MATLAB,数据库软件SQL Server 2008,办公软件Excel,都可以用来进行线性回归的分析。在此,只介绍比较有代表性的Excel和MATLAB。
2.1 使用Excel进行线性回归
Excel是微软办公套装软件的一个重要的组成部分,它可以进行各种数据的处理、统计分析和辅助决策操作,广泛地应用于管理、统计财经、金融等众多领域。利用Excel进行线性回归的优点是,方便、快捷、直观,挖掘者不需具有编程能力。但是,Excel毕竟不是专业的统计工具,其提供的回归功能仅局限于二维的状态空间,且回归的结果不够精确。
例1表1中的数据为研究某一化学反应过程中,温度x(℃)对产品得率Y(%)的影响,测得数据如下:

表1 温度与产品得率关系表
图2是利用Excel的散点图功能,将表1中的数据显示为散点图,设置“趋势线预测/回归分析类型为线性”,即得出回归方程及相关系数R的平方(R2越趋近于1表明所得回归方程越能准确的描述状态空间)。
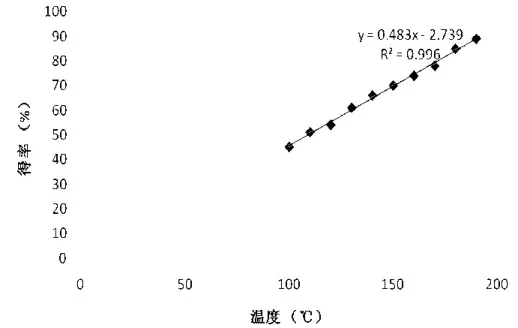
图2 温度与产品得率散点图
在Excel中,除了简单的一元线性回归模型外,还提供了一些其他的一元回归模型(如指数、对数、多项式、幂、移动平均等)。
例2表2是1957年美国旧轿车价格的调查资料,今以x表示轿车的使用年数,Y表示相应的平均价格。

表2 轿车使用年数与平均价格关系表
观测散点图,可知回归曲线大致呈指数形式,因此使用Excel中的指数回归模型求回归方程(如图3)。
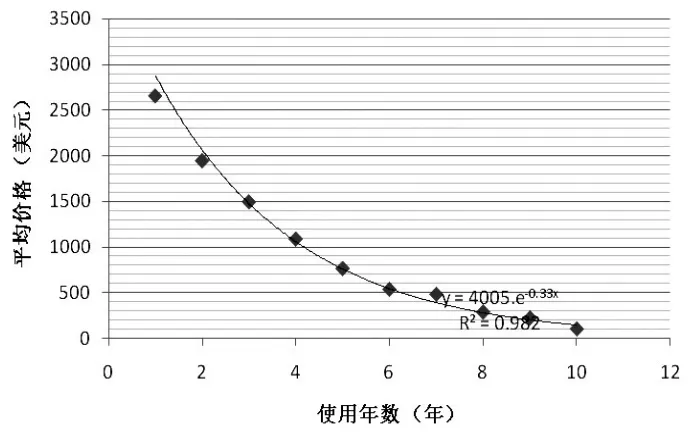
图3 轿车使用年数与平均价格散点图
Excel中所提供的预测/回归模型仅限于二维空间,但是通过使用一些插件可以进行多元线性回归估计,如StatCalc插件。
例3这里用改编自Chaterjee,Hadi和Price在大金融机构中评价管理人员的表现的例子来例示多元线性回归的过程。
表3所示的数据源自一个大金融机构的某个部门的一项对办公室工作人员调查的例子。因变量是对在该机构的管理者领导一个部门的效率的衡量,所有的因变量和自变量都是由25个雇员按照管理者工作的不同方面进行从1到5的分级。作为结果,对于每个变量的最小值为25,最大值为125。这些分级是对在30个部门,每个部门25个雇员的调查问题的回答。分析目的是探索用调查问卷方式预测部门的效率的可行性,从而避免了直接衡量效率的努力。变量是对调查问题的回答,并描述如下:Y,管理的效率衡量;X1,处理雇员的抱怨;X2,不允许有特权;X3,学习新事物的机会;X4,根据表现提拔;X5,对差的表现过于挑剔;X6,推进更好的工作的进度。
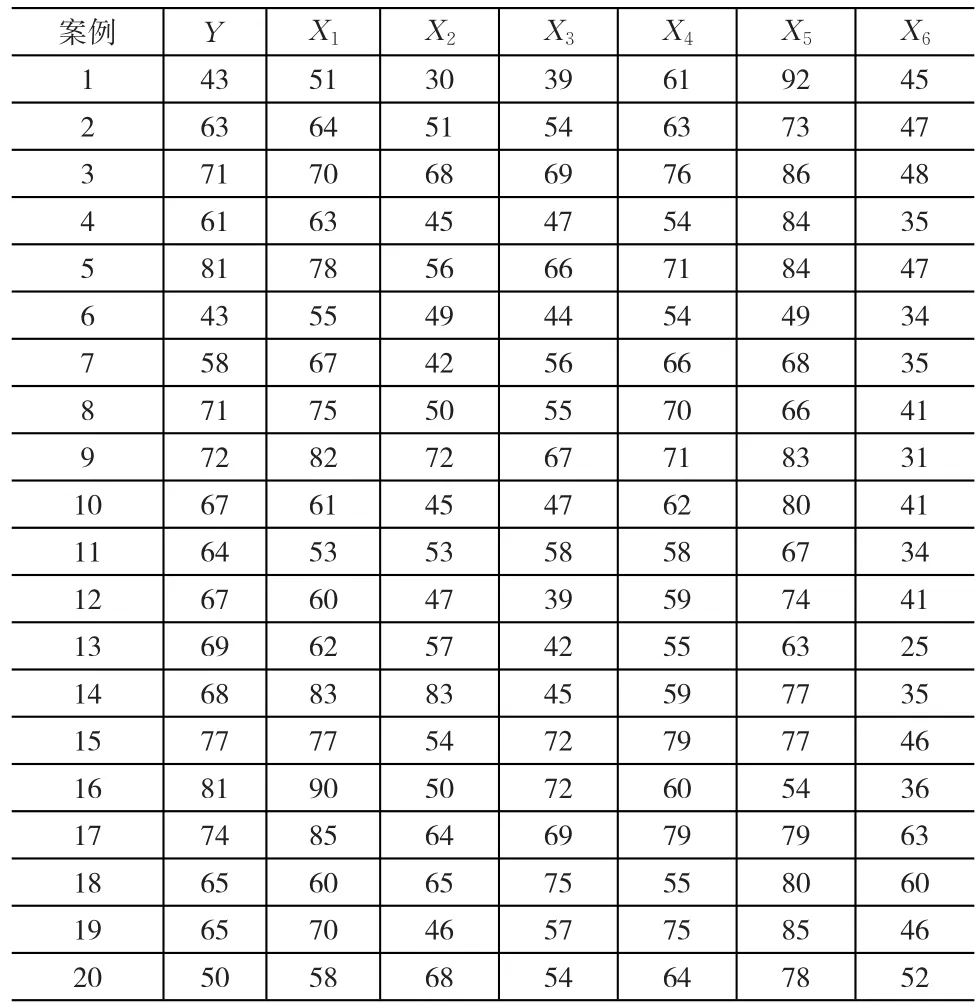
表3 管理效率衡量分析表
使用StatCalc此插件计算得出的具体结果如图10:
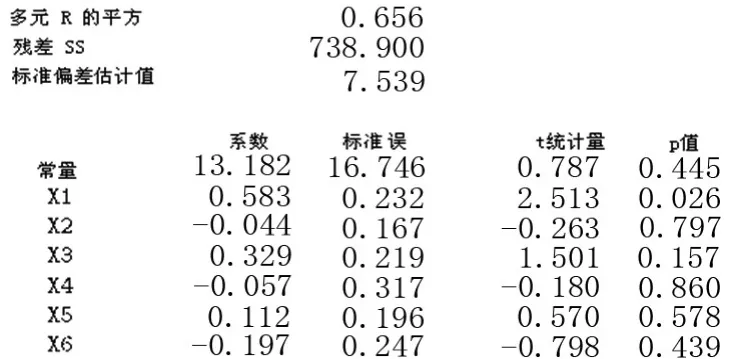
图4 StaCalc的分析结果
2.2 使用MATLAB进行线性回归
图5是对例1进行线性回归所编写的代码。从运行结果可以看出,求出的回归方程为y=-2.7394+0.4830x,与Excel所得回归方程基本一致。图6则是此段代码运行生成的源数据的散点图及回归曲线。

图5 对例1线性回归的MATLAB代码
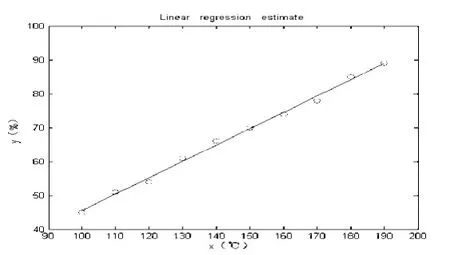
图6 MATLAB所得例1的散点图及回归曲线
图7,是对例2进行回归所编写的代码。这里,先将y取对数,求得lny与x的线性回归方程后,再还原为y与x的指数回归方程。从运行结果可以看出,求出的曲线回归方程为y=3514.3e-0.2977x,相关系数R的平方为0.9979,比Excel所得回归方程更为精确。图8则是此段代码运行生成的源数据的散点图及回归曲线。

图7 对例2线性回归的MATLAB代码
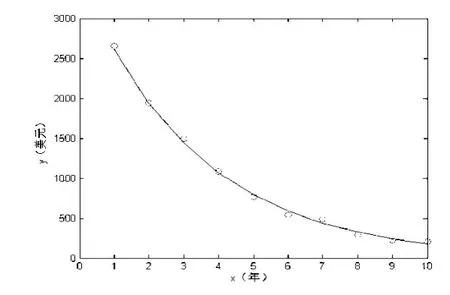
图8 MATLAB所得例2的散点图及回归曲线
图9,是使用MATALAB对例3中的数据进行多元线性回归的代码及结果。从运行结果可以看出,所得结果比图4更加精确。
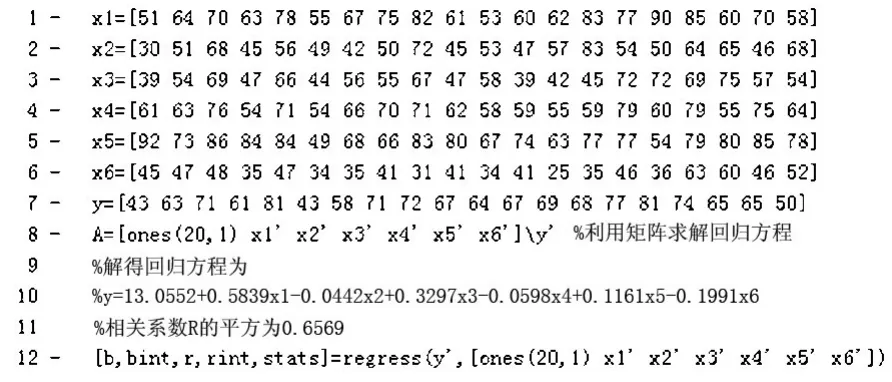
图9 对例3线性回归的MATLAB代码
3 线性回归算法的改进
3.1 分段线性回归
图10,是一状态空间的散点图。从该关系图可以看出,若使用传统的线性回归方法,使用一条连线将使得模型表示数据的效果较差。但是,如果使用两条或多条连线,则模型可以更精确地逼近数据。此时,回归方程是一种分段函数的形式。分段的线性回归模型包含2个要素——断点和回归方程,两条连线的相交点是断点,状态空间被断点分割为一个个小的子空间,再依次对每个子空间进行线性回归。以下是分段线性回归算法(DLA,Divide Linear Regression)的概要:
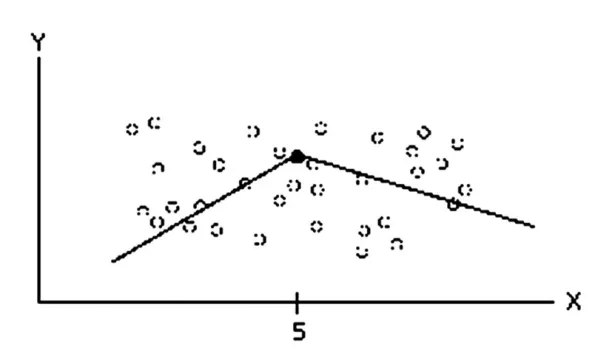
图10 分段线性回归

在此算法中,Examples是按自变量正序整理过的状态空间。由上述算法概要不难看出,分段线性回归算法比普通的线性回归算法可以更精确的描述状态空间,而对断点的寻找则成为了该算法的关键所在,断点的定义越准确,则该算法对状态空间的描述越准确。一种简单的方法就是寻找局部极值点,因为局部极值点必定为断点。对于极值点的寻找,则可以采用爬山算法来实现。
3.2 孤立点
线性回归本质上可以避免特化过渡,而与特化程度相关的最主要的问题是孤立点的出现。孤立点,是指数据点距离回归平面很远,并且在取值范围的极值附近的点,对结果的影响不均衡。举个例子,有这样一组数列:1,2,3,4,5,6,7,8,9,1000。该数列的取值范围是从1到1000,然而该数列中的数据集中在其中1%的范围内。数列中的1000很显然是一个孤立点,因为它孤立于数列中所有的其他值,但并不能说它是误差或错误数据,它甚至可能是完全正确的数据。比如保险索赔,大部分都金额较小,而小部分金额巨大。如果把孤立点一起列入线性回归的状态空间里,则肯定会影响最终回归的结果。
对于孤立点的处理,可以考虑两种方法。一种方法可以称之为邻域查找法(NC,Neighborhood-Check),它是通过邻域的方法来定义孤立点,当一个数据点在某个半径的范围内没有其他的数据点存在时,可以认为其为孤立点。这种方法,直观、简单,但是开销会很大,而且只能找出孤立点,而不能对其进行处理。
另一种方法可以称之为等频率分箱法(ESB,Equivalent Sub-Boxes),它是将状态空间在观测值的取值范围内进行等频率的分割成若干箱。以上文中的数列为例,假设将其分为100箱,则可分割为1~10、11~20、…、991~1000,100个等范围的状态空间,那么只有第一个箱子有9个数据、最后一个箱子有1个数据,其他箱子都是空的。这时再进行线性回归,只需要面对一组包含9个值的状态空间,和一个孤立点。但是,此数列若为7、8、9、10、11、12、13、14、15、1000,那么会有3个箱子有数据,且1~10和11~20的箱子中的数据线性相关度是很高的。因此,为了避免上述情况的出现,在分箱之后还应再将线性相关的箱进行合并。以下是该算法的概要:


在此算法中,Examples为状态空间,k为需要进行分箱的个数,num是判定箱中的数据是否为孤立点的依据。
4 小结
线性回归只是发现线性关系,其对于数据的异常变动(比如孤立点)很敏感,尽管也有算法的健壮版本可用,但总体说来它们对于波动不太敏感。线性回归问题对于输入变量的共线问题消化不良,不能处理缺失数据。此外,线性回归只是产生解释,对于数据集结构的很小变化可能高度敏感,而对于增量式的交互作用的敏感性却很强。
虽然,线性回归有许多局限性,但是不可否认的是,线性回归快速并且容易,并且一旦得到对于结果的解释,会产生许多有用的信息。尽管大多数真实世界环境有明显的非线性本质,但一个挖掘者在业务数据中所遇到的大多数关系最后是线性的、部分线性的、半线性的,或者是可线性化的。因此,在数据挖掘领域,线性回归始终占有着重要地位。
[1]DORIAN PYLE.业务建模与数据挖掘[M].杨冬青,马秀莉,唐世渭,译.北京:机械工业出版社,2005.
[2]盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2005.
[3]BERNARD W.TAYLOR III.数据、模型与决策[M].侯文华,译.北京:机械工业出版社,2008.
[4]华德宏,刘 刚,兰家隆.一种改进的一元线性回归算法[J].现代电子技术,2006,7:63-68.
[5]PART-ENANDER,E.,Sjoberg,A..MATLAB 5手册[M].王艳清等译.北京:机械工业出版社,2000.
