投资组合保险策略绩效的随机占优比较方法
2012-01-07张秀丽
张秀丽
(郑州大学 商学院,郑州450001)
0 引言
投资组合保险策略大致分为两类,一类是源于Black-Schole期权定价的策略如OBPI,另一类是设置简单参数的策略如CPPI策略。二者虽然都是保险策略,但是在不同市场的绩效不同,何朝林、孟卫东(2006)认为CPPI策略优于OBPI策略;Cesari和Cremonini(2003)采用MonteCarlo模拟认为在熊市和市场震荡时,CPPI策略优于其他策略。但是以上绩效的比较基本上是基于平均超额收益率、标准差、SHARPE比率等指标。而投资组合保险策略的收益率并非服从正态分布,因此,能够完全描述正态分布特征的均值与标准差未必是合适的度量标准。崔晓东和郑玉华(2009)、Annaert、Osselaer和Verstraete(2009)采用随机占优准则作为投资组合保险绩效评价的标准。令人遗憾的是作为实证检验却未给出p值,而只是给出了随机占优关系。本文将以上证指数为风险资产,尝试给出策略之间接受或拒绝随机占优假设的p值,并比较不同指数如上证50、上证180、沪深300作为投资组合保险策略的风险资产是否存在优劣关系。
1 投资组合保险策略收益率的统计描述
基于Black-Schole期权的投资组合保险策略(OBPI)是将份额为
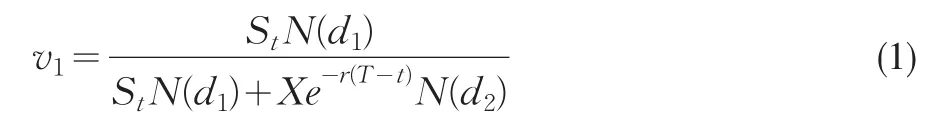
的资产投资在风险资产上,其余资产投资在无风险资产上。其中,St为t(0≤t≤T)时刻证券价格,X是期权的执行价格,N(·)是标准正态累积分布函数,T为到期日,r为无风险收益率。
OBPI策略需要随着证券价格的变化而不断调整投资在风险资产与无风险资产的份额。
固定比例投资组合保险策略(CPPI)克服了OBPI策略参数较多,计算复杂的特征,而仅仅依靠设置简单参数将资产在无风险资产与风险资产之间分配,达到保险的目的。投资于风险资产的部分为Et=M(At-Ft),其余资产投资在无风险资产上,由于证券价格变化,从而导致总资产At变化,反映投资者风险态度的M和要保金额Ft不变,从而引起在风险资产与无风险资产之间的分配不断变化,捕捉市场上升的机会或避免市场下降的损失。
时间不变性投资组合保险策略(TIPP)策略是较CPPI更为保守的策略,它的要保金额是变动的,在当前资产的组合价值的固定比例与上期要保金额之间选择一个较大值作为本期要保金额,见式(2)。

其中,f是固定要保比率,Dt是t期在无风险资产上的投资。
以上策略均为投资组合保险策略,执行策略后,收益率不再服从正态分布,如图1所示。图1的投资组合保险收益率是以2005年4月11日~2011年4月11日的沪深300指数作为风险资产而得到的。
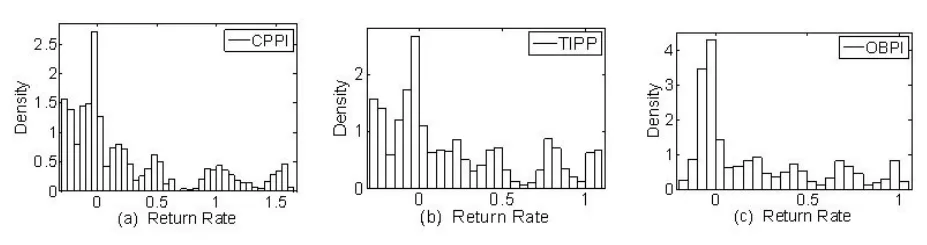
图1 投资组合保险策略CPPI、TIPP、OBPI的年收益率密度函数
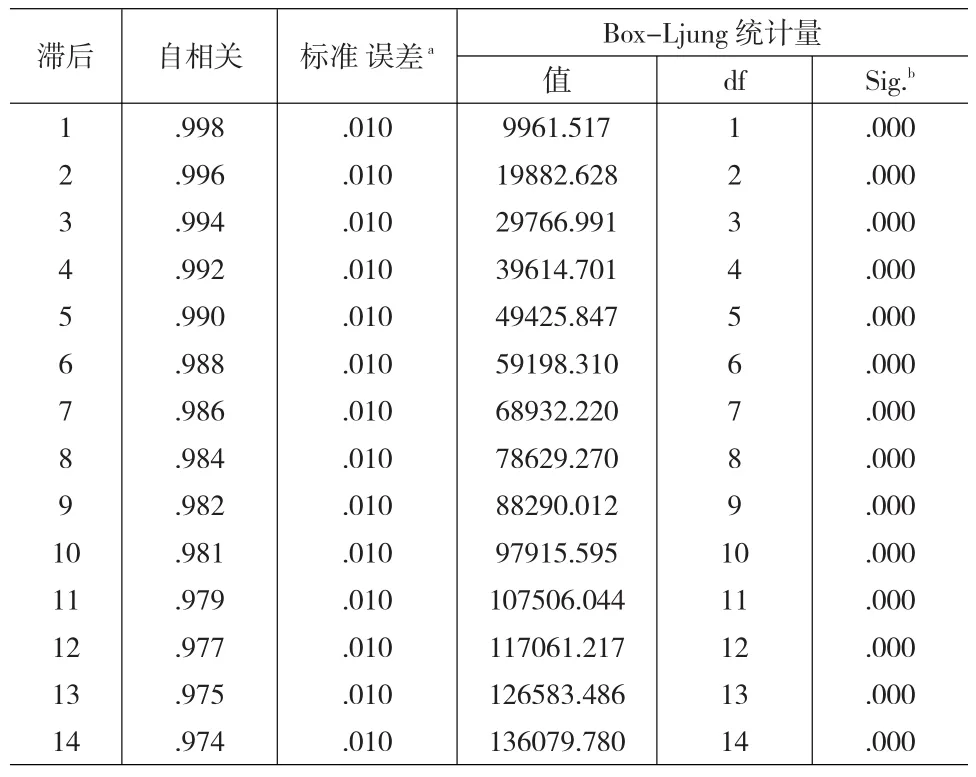
根据Box-Ljung检验,CPPI策略的收益率之间存在较强的相关性,如图2所示。TIPP策略、OBPI策略的收益率与此类似,也存在较强的序列相关性。
序列:CPPI 自相关图
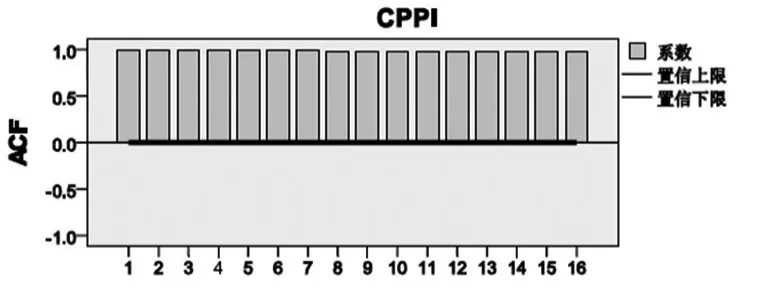
图2 CPPI策略收益率的自相关函数
实际上,上述不同投资组合保险策略收益率之间不仅存在较强的序列相关性,而且存在较强的交叉相关性,可以计算出其交叉-相关矩阵为:

投资组合保险收益率之间存在高度相关性。因为这几种策略的风险资产是相同的,只是份额不同而已。
2 随机占优的实证检验
随机占优准则因其独立于效用函数仅根据分布函数就给出偏好顺序,一直受到决策者的青睐,是决策领域的重要准则。
定义1假设有两个随机变量X和Y,其相应的累积分布函数为G1和G2,则X一阶随机占优于Y的充要条件是G1(t)≤G2(t),对于所有的t存在且至少在一点严格不等式成立。记为X≻FSDY。
相应的k阶随机占优定义为:
定义2假设有两个随机变量X和Y,其相应的累积分布函数为G1和G2,则X k阶随机占优于Y的充要条件是,对于所有的t存在且至少在一点严格不等式成立。
随机占优准则虽然在理论上很受欢迎,但是在实证中的应用一直受到限制,主要原因是抽样误差的存在。可喜的是在观察值独立同分布的条件下,McFadden(1989)建议采用Kolmogorov-Smirnov检验一阶、二阶随机占优准则,随后其他研究者在此基础上进一步完善随机占优准则的实证检验,其中比较典型的有Davison和Duclos(2000),他们给出了实证检验的非常有用的表达式:
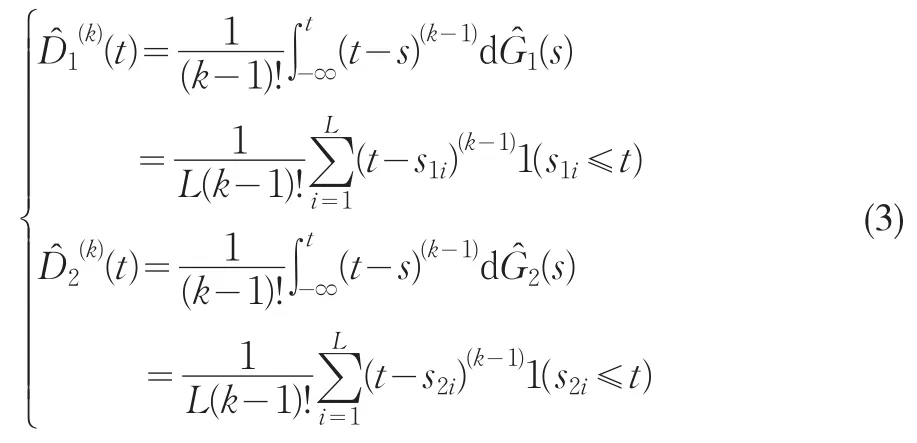
G1(t)、G2(t)的经验分布函数为:
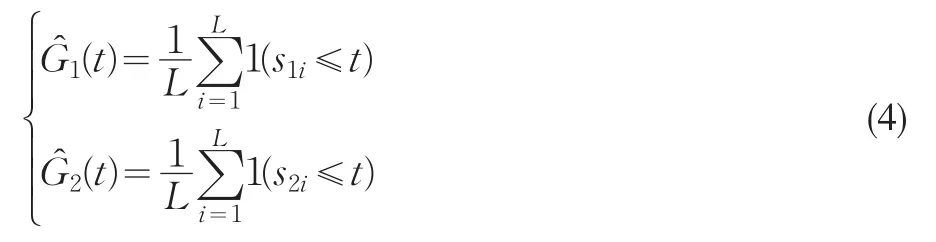
其中,s1i、s2i分别是随机变量X和Y的第i个观察值,1≤i≤L,L为样本数据个数;1为示性函数。如果
则X k阶占优于Y。如果k=1,则意味着
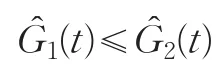
Linton、Maasoumi和Whang(2005)提出采用subsample方式进行随机占优检验。其假设为:
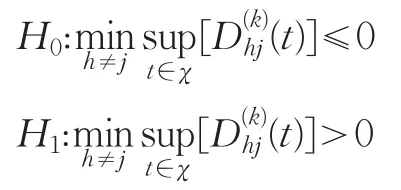
这种抽样检验方式适于时间序列存在自相关以及序列之间存在互相关的情况。本文考察的投资组合策略的绩效具有这一特征,因此本文的实证检验采用subsample方式,而不是bootstrap方式。
计算统计量
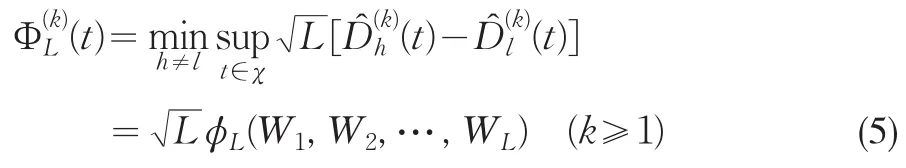
的分布函数采用subsampling方式:子样本大小为b,根据Klaver(2005)的研究,b的取值最好为。则统计量ϕb可以由大小为b的子样本{Wi,Wi+1,...,Wi+b-1}得到,即
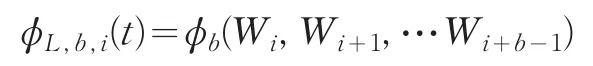
其中,i=1,…,L-b+1。这样,就可以由
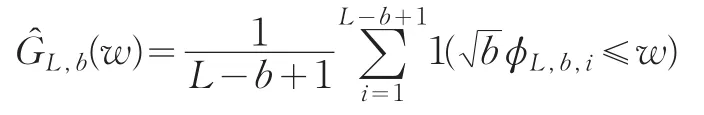
来近似ΦL的分布函数GL。
则检验中是否拒绝零假设的p值为:
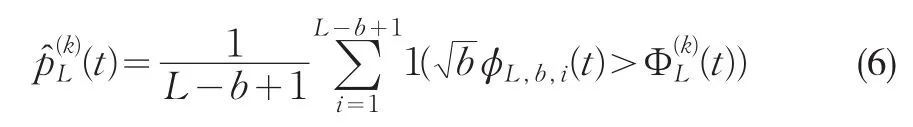
如果p值很小,p≤0.05,则在0.05的水平上拒绝原假设,即不存在随机占优关系。
3 实证设计
沪深300的数据开始于2005年4月11日,因此本文所有的数据均开始于2005年4月11日,结束于2011年4月11日,共计6年的时间。
初始资产为1亿元,对于OBPI来说要保证其资产不低于期初资产。根据式(1)可以计算出投资于风险资产的份额v1。为方便比较,对于CPPI及TIPP策略来说将同样比例的资产投资于风险资产。由Et=M(At-Ft)知,同样的Et可以对应着不同的M与Ft的组合。本文实证研究表明,当M取2、3、4时,与相应的Ft组合所形成的不同CPPI策略之间不存在随机占优关系,当M=2时收益率较高,因此采用M=2的组合。TIPP策略中,固定要保比率设为f=0.75。无风险收益率参考一年期固定存款利率,自2005年4月11日~2011年4月11日,一年期固定存款利率由2.25%变动到4.14%,变动次数达15次之多。为简便计算,本文采用其加权平均值,即2.75%,连续复利计息。
投资组合采用每天调整一次以接近连续调整。考虑交易成本,设交易成本为交易金额的0.5%,OBPI策略的交易成本通过调整波动率处理,即
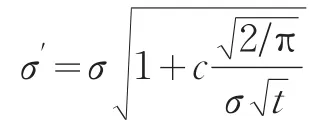
上式中,c为相对交易成本,取值为0.5%,σ为调整前的波动率,根据投资组合保险策略开始前一年的风险资产收益率数据计算得到。σ′为调整后的波动率。
由于本文是通过随机占优评价投资组合保险策略的绩效,因此需要大量的样本数据,而不能仅仅考虑某一上升或下降或震荡时期的情况。因此,投资组合保险策略的收益率计算采用Block Bootstrap抽样方法,区组长度为一年,随机抽取开始日期,根据其后一年的证券资产的收益率进行一年的投资组合保险策略模拟,这样的过程进行10000次。
本文的计算采用MATLAB2009软件进行。沪深300、上证50及上证180的数据均来源于雅虎财经网站。
4 实证结果分析
表1、2、3分别为沪深300、上证50、上证180作为风险资产时,各种投资组合保险策略的绩效,并与B&H及CM策略进行比较,评价标准为传统的年平均超额收益率、标准差、SHARPE比率。可以看出,投资组合保险策略CPPI及OBPI具有较高的年平均超额收益率、较大的SHARPE比率,同时波动性也较大。
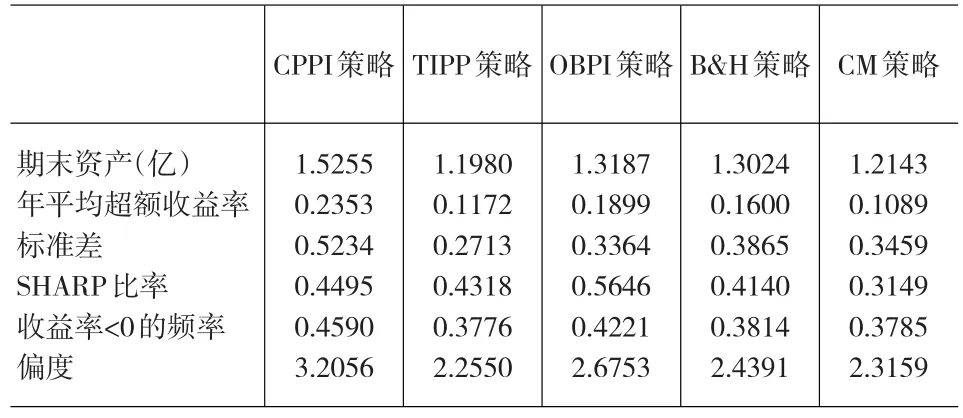
表1 沪深300为风险资产的各种投资组合策略的绩效比较
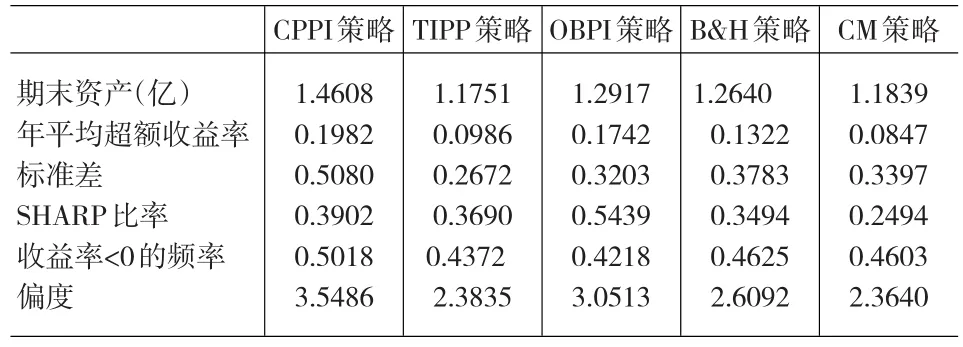
表2 上证50为风险资产的各种投资组合策略的绩效比较
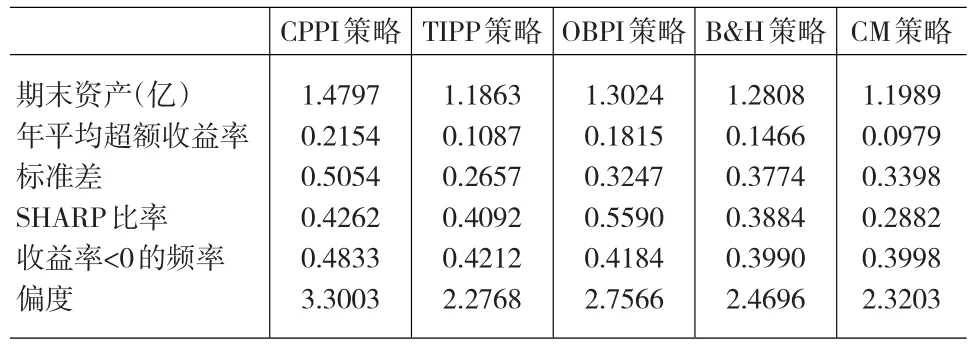
表3 上证180为风险资产的各种投资组合策略的绩效比较
表4、5、6分别是风险资产为沪深300、上证50、上证180时各种策略之间的随机占优关系,其中FSD表示一阶随机占优,SSD、TSD分别为二阶、三阶随机占优。可以看出,除TIPP策略与B&H策略相当以外,投资组合保险策略随机占优于其他策略,OBPI策略一阶随机占优于CPPI、TIPP策略,当风险资产为沪深300、上证180时,CPPI策略三阶随机占优于TIPP策略。
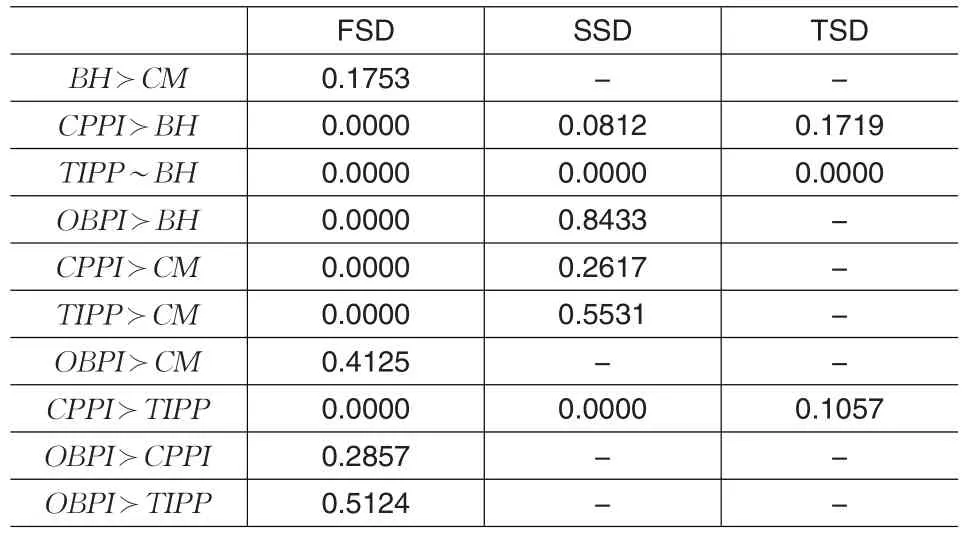
表4 各种策略直接之间的随机占优关系 (风险资产为沪深300)
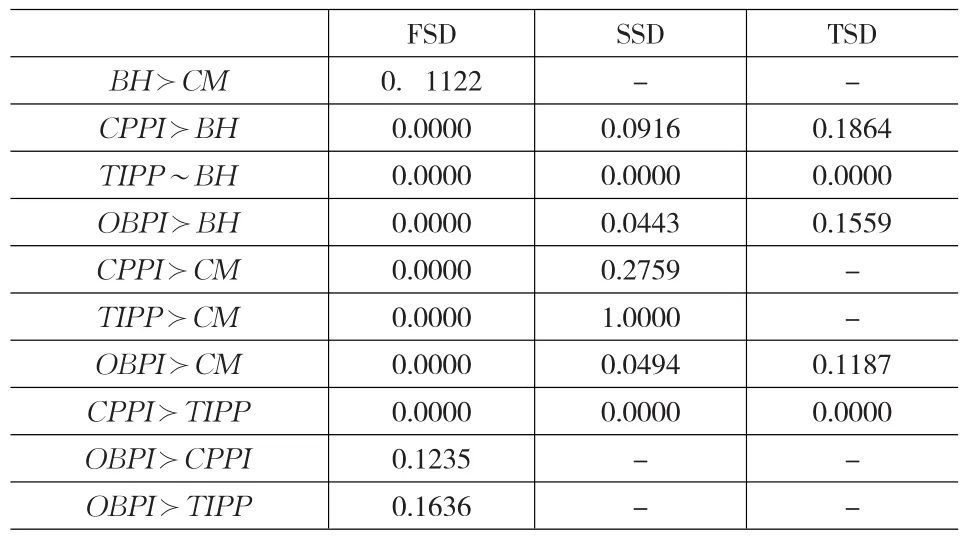
表5 各种策略直接之间的随机占优关系 (风险资产为上证50)
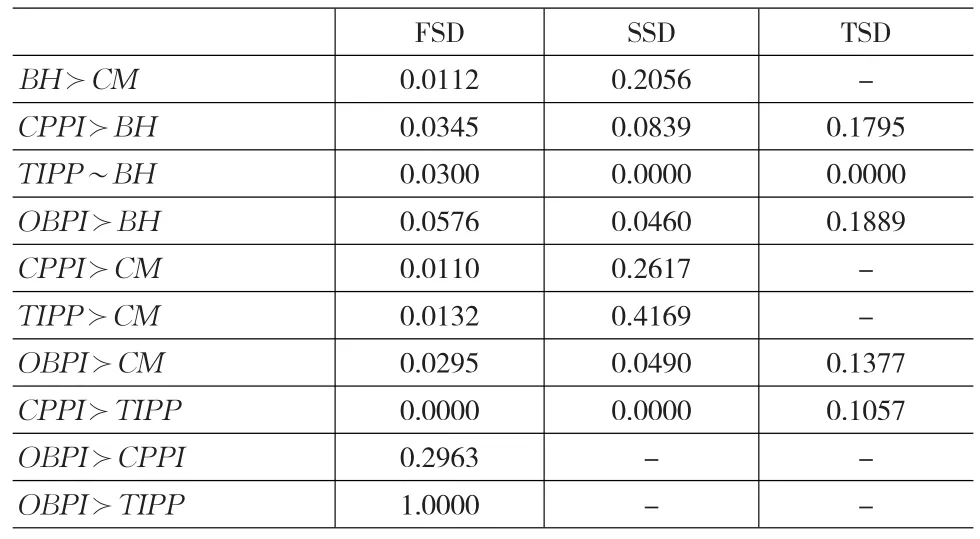
表6 各种策略直接之间的随机占优关系 (风险资产为上证180)
表7为不同风险资产的CPPI策略绩效的传统评价。可以看出,当风险资产为沪深300时其年平均超额收益率、SHARPE比率要高,但相应的标准差也大。类似的,对于TIPP策略和OBPI策略也存在当风险资产为沪深300时,有较高的年平均超额收益率、SHARPE比率,较大的标准差。

表7 不同风险资产的CPPI策略绩效比较
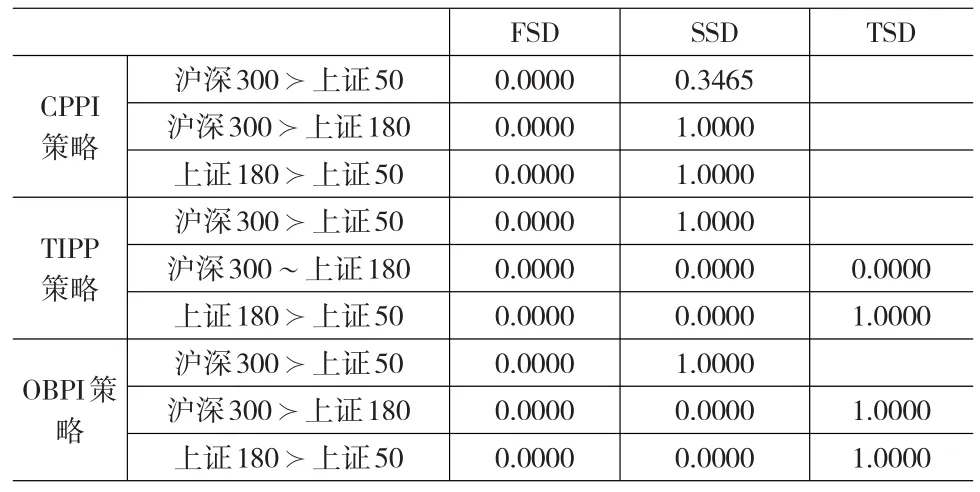
表8 在同一保险策略下不同风险资产之间的随机占优比较
表8是在同一投资组合保险策略下,由于风险资产不同而进行的策略绩效比较。可以看出,无论哪种策略下,沪深300作为风险资产要随机占优于上证50,在CPPI、OBPI策略下,上证50最不应当作为风险资产;而在OBPI策略下,最好选择沪深300作为风险资产。
5 结束语
在进行投资组合保险策略的绩效评价时,由于策略规避下方风险的特性,收益率不再服从正态分布,因此传统的绩效评价准则均值、方差及基于此的SHARPE比率的有效性受到质疑。而基于分布的随机占优准则是一个较好的选择。由于比较的策略存在较强的序列相关性及交叉相关性,本文在随机占优的实证应用中采用subsample的方式研究投资组合保险策略之间的随机占优关系,同时研究了中国证券市场的三个主要指数作为风险资产,各种投资组合保险策略绩效之间的随机占优关系。可以看出,投资组合保险策略随机占优于非保险策略;产生较晚的沪深300指数作为投资组合保险的风险资产随机占优于其他指数。
[1]Linton,O.,Maasoumi,E.,Y.J.Whang.Consistent Testing for Stochas⁃tic Dominance under Genenral Sampling Schemes[J].Review of Eco⁃nomic Studies,2005,(72).
[2]Klaver,H.Testing for Stochastic Dominance Using Circular Block Methods[J].Graduate School of Risk Management,University of Co⁃logne,2005,(6).
[3]Linton,O.B.,T.Post,Y.J.Whang.Testing for the Stochastic Domi⁃nance Efficiency of a Given Portfolio[M].Mimeo:London School of Eco⁃nomics,2005.
[4]何朝林,孟卫东.构建证券组合保险的策略分析[J].重庆大学学报,2006,(29).
[5]崔晓东,郑玉华.投资组合保险策略的随机占优检验[J].系统工程,2009,(27).
