CAPM在深市A股地产股的实证分析

王 军，耿 建

（中国石油大学（华东）经济管理学院，山东青岛266555）

1 资本资产定价模型（CAPM）

Sharpe(1964)、Litner(1965)和 Mossin(1966)提出了资本资产定价模型（Capital Asset Pricing Modle,简称CAPM），导致了现代资产资本定价模型的形成。CAPM作为近年来发展最快的金融领域之一，与APT（套利定价理论）、OPT（期权定价理论）共同构成现代金融理论的三大基石，其理论基础是Markowitz的均值-方差投资组合理论。

CAPM是建立在以下四条基本假设条件基础上的，即：

（1）投资者是理性的，以均值-方差有效组合为效用最大化投资组合；

（2）投资者对市场存在一致预期性；

（3）市场存在无风险收益率，投资者可以无风险收益率进行无限借贷；

（4）市场无摩擦，不存在交易成本等。

CAPM的数学表达式为：

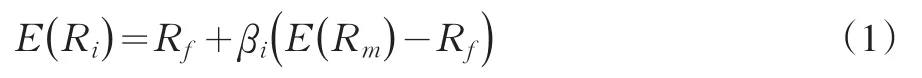
其中，E(Ri)为证券i的期望收益率；Rf为无风险收益率；E(Rm)为证券市场组合的期望收益率；为证券系统风险的测度。

若同时考虑时间因素，则（1）式为：

其中，E(Rit)为证券i在t时间段的期望收益率；Rft为t时间段的无风险收益率；E(Rmt)为证券市场组合在t时间段的期望收益率；βi为证券系统风险的测度。将(2)式作简单变形如下：

其中，Rit=E(Rit)-Rft；Rmt=E(Rmt)-Rft；αi、βi为系数；εit为随机误差项。

若要接受CAPM，则实证结果需要同时满足以下两个条件：

（1）回归方程（4）的截距项αi必须等于或近似等于零，即接受H0：αi=0的假设；

（2）对于不同的证券或证券组合而言，其超额收益E(Rmt)-Rft应该只能用βi来解释，对方程（4）进行回归时Rmt应该与βi存在线性关系，即拒绝H1：βi=0的假设。

2 CAPM对深市A股地产股的实证检验

2.1 研究方法

本文在对CAPM进行检验时应用时间序列与横截面的最小二乘法的线性回归的方法。时间序列的线性回归主要用于β值的估计，而横截面回归的方法则主要用于CAPM的统计检验分析。

2.2 数据选取与处理

本文以2008年1月1日至2010年12月31日在深市A股上市的30支地产股的周收盘价为研究对象，这一时期正是金融危机过后我国股票市场的不景气和调整时期，对这一时期进行研究更加贴近实际经济状况，这强化了研究的实用性和指导意义。深市A股共59只地产股，其中ST珠江（000505）、ST东源（000656）及ST重实（000736）三只ST股未考虑，合肥城建（002208）、滨江集团（002244）、世联地产（002285）及南国置业（002305）四只股票在2008年1月1日后上市故剔除，还有一些股票像荣安地产（000517）、中润投资（000506）、高新发展（000628）等缺失数据比较严重也予以剔除，在余下的地产股中随机抽取30支作为样本股。数据来自青岛中信万通有限公司提供的通达信证券交易平台。选取深证成指作为市场组合指数，并用深证成指收益率代表市场组合收益率。为避免股票的派息、配股、送股以及股票分割对数据造成的影响，在选取样本时对于样本股票进行了前复权处理。每支股票计算周收益率，其计算公式如下：

其中，pit是第i支股票在t周的收盘价；pi(t-1)是第i支在t-1周的收盘价。

若个别股票数据缺失，则视本周收盘价与上周收盘价相同。对于无风险收益率，通常采用一年期国债利率或银行间同业拆借利率替代。本文采用一年期的居民存款利率3%作为无风险利率，其中一年按十二个月计算，每个月按四周，这样计算的无风险利率为0.0625%。分析软件为Eviews6.0。

2.3 单只股票及证券组合β系数的估计

在估计单只股票βi时采用单指数模型：Rit=αi+βiRmt+εit，符号意义见公式（4）。进行一元线性回归，可得βi系数估计值，表示该只股票的系统风险测度。

考虑到单只股票的非系统性风险较大，CAPM检验偏差较大，常用构造股票组合来分散掉大部分非系统性风险而研究系统性风险与收益的关系。本文按照个股的β系数大小这一基准进行股票组合的构造。组合构造出后就可以计算组合的收益率并估计组合的β系数。股票组合β系数的估计，运用时间序列模型：

其中，Rpt为t时间投资组合的收益率；Rmt为深证成指收益率；αp、βp为系数，εpt为残差项。本文中的组合均为等权组合，其收益率计算公式如下：

2.4 实证检验步骤

为了减少回归检验中的误差，把检验分为以下几个步骤：

2.4.1 把时间段分为三个时期：2008年1月1日至2008年

12月31日；2009年1月1日至2009年12月31日；2010年1月1日至2010年12月31日。

2.4.2 利用第一时期的数据运用OLS法进行时间序列回归，并按以下公式计算单只股票的βi值：Rit=αi+βiRmt+εit；其中，Rit为股票i在第t周的收益率；Rmt为第t周市场收益率。回归结果如表1所示。

表1 30支深市A股地产股回归结果汇总表

2.4.3 依照第2步估计出的单只股票的βi值从小到大的顺序排列，并分成6个股票组合，每组含5支股票。组合结果使βi最小的5支股票分在第一组合，使βi最大的5支股票分在第六组合，构造的股票组合结果如表2所示：

表2 对30支深市A股地产股进行股票组合构造表

2.4.4 根据第二期的数据，对组合的收益率与市场收益率运用OLS法进行时间序列回归，并按以下公式计算每个组合的βp值及回归残差的标准差σp：Rpt=αp+βpRmt+εpt；其中，Rpt为组合在第t周组合的平均收益率；Rmt为第t周市场的平均收益率。数据回归的结果统计如表3所示：

表3 6个股票组合的回归结果汇总表

2.4.5 风险与收益关系的检验。根据第三期各组合的周平均收益率和第4步计算所得的各组合的βp值及回归残差的标准差σp进行横截面数据回归。所需的数据计算结果如表4所示：

表4 组合周平均收益率和βp、σp汇总表

分别对以下5个方程进行回归分析其中，Rpi是2010年平均周收益率；βpi是组合i的β系数，λ0、λ1是待估计参数，εi为残差，σpi为非系统风险。

首先，采用标准的证券市场线SML的回归方程：

回归结果如表5所示。

表5 方程（8）的回归结果

回归结果显示：R2=0.035301，调整的R2=-0.205874，说明整体显著性很差，样本的拟合度弱；且常数项与自变量的P值均远大于一般的临界值0.05,说明变量的显著性同样很差，即股票的收益与风险关系不显著，同时λ0为负值与无风险收益率0.000625存在偏差说明市场存在一定的投机行为，λ1为负值说明股票系统风险越大收益率越高，这有悖与CAPM的预期即风险与收益呈正比。因此，股票组合的收益与市场系统风险不存在线性关系，从而否定了CAPM在深市A股地产股有效性。

其次，在方程（8）加入新的解释变量σpi得另一回归方程：

回归结果如表6所示。

表6 方程（9）的回归结果

回归结果显示：R2=0.044379，调整的R2=-0.592701，说明方程整体显著性很差，样本的拟合度弱；且常数项与两个自变量的P值均远大于一般的临界值0.05,说明变量的显著性同样很差，即股票的收益率与系统风险和非系统性风险均相关性不强。

回归结果如表7所示。

表7 方程（10）的回归结果

回归结果显示：R2=0.653207，调整的R2=0.422012，尽管较前两个方程整体拟合有度有所提高但仍然较低，说明方程整体显著性还是不显著；且常数项与两个自变量的P值仍大于一般的临界值0.05,接受原假设即变量不显著。接着，考虑σpi为唯一解释变量时的回归方程：

回归结果如表8所示。

表8 方程（11）的回归结果

回归结果显示：R2=0.000391，调整的R2=-0.249511，说明方程整体显著性很差，样本的拟合度弱；且常数项与自变量的P值均远大于一般的临界值0.05,说明变量的显著性同样很差，即股票的收益率非系统性风险均显著性差，非系统风险仍然不能很好解释收益率的波动。

最后，在方程（10）中加入σpi得回归方程：

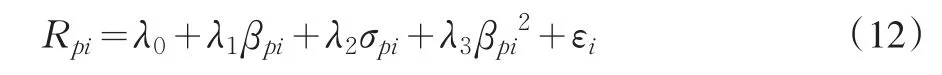
回归结果如表9所示。

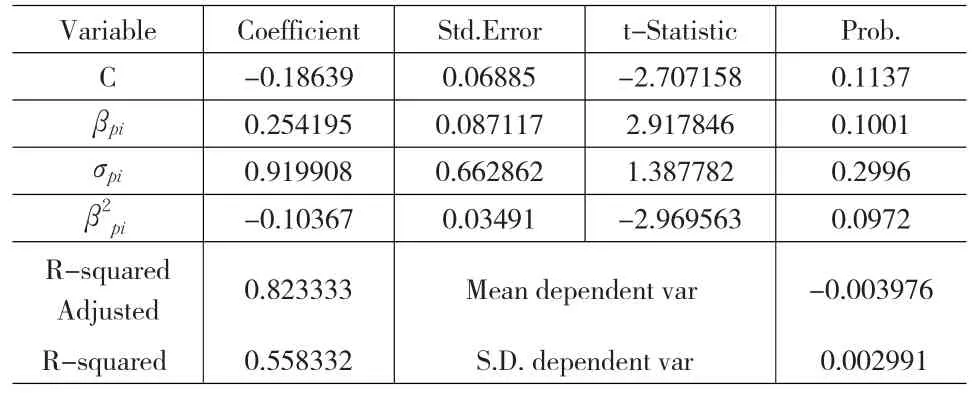
表9 方程（12）的回归结果

回归结果显示：尽管R2=0.823333，调整的R2=0.558332，及各变量的P值相比前面的方程均有所改进，但方程整体及各变量均不显著，方程的自变量对收益率因变量解释力均不足。

根据以上对方程（8）～（12）的回归结果深市A股地产股的收益与市场收益、系统风险、非系统风险等都没有严格的线性关系，CAPM不适用深市A股地产股的估值。

3 结论及政策建议

本文对深市A股地产股进行时间序列及横截面的检验结果表明：（1）如果对股票进行一定的组合确实符合CAPM理论可以在一定程度上消除非系统风险；（2）股票的收益与系统性风险线性关系不显著，这与CAPM理论相悖；（3）λ0的估计值与无风险利率相差较大，说明股票市场存在较大的投机性，投资者追求的不是资金的时间价值而更多的是高风险所带来的高收益。简而言之，尽管中国A股经过近20年的发展取得了一些成绩，但是市场效率及成熟度仍然较低，没有通过CAPM实证检验。

通过对比2009年与2010年β值发现，2010年相对于2009年均有所减少且均小于1，说明深市地产股由2009年的进攻型股票转为2010年的防守型股票，这可与我国在2010年出台了一系列房贷政策有关，这一系列的政策遏制了我国房地产市场疯长的势头，打压了膨胀的房市泡沫。

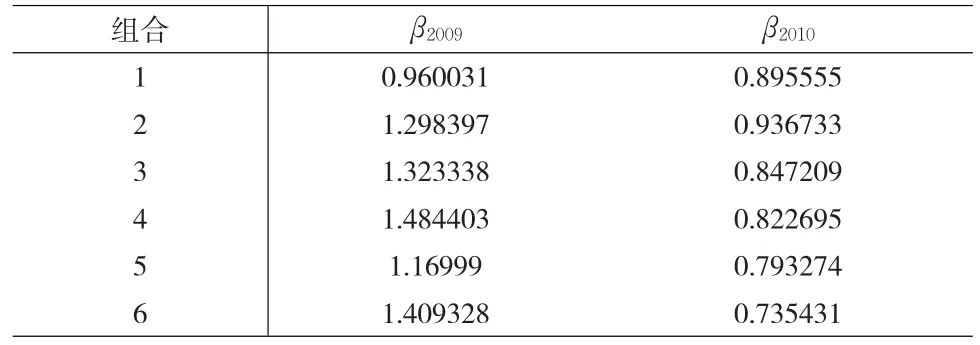
表10 β2009与 β2010对比

2010年深市A股地产股的组合βp值均小于1，股票的防御性增强，这说明政策已经初见成效，房地产市场已经不再随市场风险的起伏而剧烈波动，而是趋于平稳，抗风险能力得到了提升。因此在政策面上还要密切关注房市的走向，在已取得的成绩下防止其反弹，必要时还要加大打压力度。从长期发展来看，政策制定者要放远眼光，积极探索住房保证政策的完善制度，保证住房长期上的供需平衡，稳定我国房市及股市的发展。

[1]Sharpe,William F.Capital Asset Prices:A Theory of Market Equilib⁃rium under Conditions of Risk[J].Jour.Nal.of Fina Nce.,1964,（19）.

[2]Fama,Eugene F.,James MacBeth.Risk,Return,and Equilibrium:Em⁃pirical Test[J].Jour.Nal of Political Economy,1973,（81）.

[3]叶晨.CAPM模型在深圳A股市场的实证检验[J].中国城市经济,2010，（12）.

[4]王璐,王玉静.CAPM模型及实证研究[J].劳动保障世界(理论版),2010，（11）.

[5]朱顺泉.资本资产定价模型CAPM在中国资本市场中的实证检验[J].统计与信息论坛,2010，（08）.

[6]顾荣宝，刘瑜华.CAPM对深证股市的实证分析[J].安徽大学学报（自然科学版），2007，（2）.

[7]靳云汇,刘霖.中国股票市场CAPM的实证研究[J].金融研究，2001，253(7).

[8]陈小悦，孙爱军.CAPM在中国股市的有效性建议[J].北京大学学报（哲学社会科学版），2000，（4）.