基于粒子群算法的关键链多项目调度管理

林晶晶，周国华

（西南交通大学a.公共管理学院，b.经济管理学院，成都 610031）

0 引言

关键链项目管理方法是将约束理论成功应用于项目管理领域而产生的一种全新的项目计划调度方法[1]。约束理论是Goldratt于20世纪70年代末期基于OPT系统发展起来的。该理论认为系统的制约因素决定系统的有效产出。因此，将管理重点放在系统的制约因素上，通过改进制约因素达到最大的有效产出。以TOC为理论基础所提出的关键链方法自产生之初便引发了企业界和学术界的广泛关注，被认为是21世纪项目管理领域的一个重大突破，并成为项目管理领域的研究热点问题[2,3]。

目前关于关键链项目管理的研究大都基于单项目环境，对关键链方法进行理论基础的分析和探讨[1-3]，在此基础上对关键链的识别和缓冲区的设置展开研究[4,5]。相关文献的研究表明，采用CCPM能有效地降低项目受不确定性因素影响的程度和改善项目计划，并已在进度、成本、范围和绩效管理等方面获得了成功应用[4]。

近年来，关键链方法运用于多项目管理的研究较少，大都从定性的角度开展了研究[5～9]。在定量方面，目前的研究主要集中于瓶颈资源约束下多项目工序的排序[10,11]。本文基于现有研究成果，探讨单瓶颈资源约束下关键链在多项目中应用的理论基础，考虑不同项目的重要性及项目完工提前或滞后的奖惩，研究满足系统总收益最大化目标的瓶颈资源分配计划；并将粒子群算法引入到关键链多项目管理的优化问题中，以期提供一个新的解决思路。

1 关键链方法

1.1 关键链方法在单项目环境中的应用

关键链方法是将约束理论成功应用于项目管理领域而产生的一种全新的项目计划调度方法。约束理论（Theory of Constraints，TOC）是Goldratt于20世纪70年代末期基于OPT系统发展起来的，认为系统的制约因素决定系统的有效产出。因此，将管理重点放在系统的制约因素上，通过改进制约因素达到最大的有效产出。

作为TOC在项目管理中直接应用产生的关键链方法与关键路径方法不同的是，强调制约项目周期的是关键链而非关键路径，关键链是既考虑工作间的依赖关系又考虑资源间依赖关系的最长的工作序列。Goldratt认为由于项目存在的不确定性和墨菲定律，在估计项目持续时间时，通常会在每个工序上都加入安全时间。但实际上，由于学生综合症及帕金森定律、多任务以及工作间的依存关系等多种因素的存在，工序上加入的安全时间常常被浪费，导致项目工期拖延。因此，基于工序工期呈正态分布的假设，Goldratt提出以50%可能完成的时间作为工序工期的估计，并以此建立工作网络图；同时考虑工序间紧前关系约束和工序间的资源约束来确定关键链，如果存在多条关键链就任意选择一条。然后通过项目缓冲、输送缓冲和资源缓冲机制来消除项目中不确定因素对项目计划执行的影响，保证在确定环境下编制的项目计划在动态环境下的顺利执行和关键链所需资源能够及时获取。

1.2 关键链方法在多项目管理中的应用

关键链多项目进度管理方法不仅能够很好减弱项目间的关联效应和不确定因素的影响，消除项目成员的不良工作行为，缩短项目的工期，而且能够较有效地解决项目间的资源冲突，改善多项目的执行环境[9]。由于TOC方法在单项目与多项目环境下的应用各有侧重点[7]，因此也决定了关键链在单项目与多项目中应用的不同。（见表1）

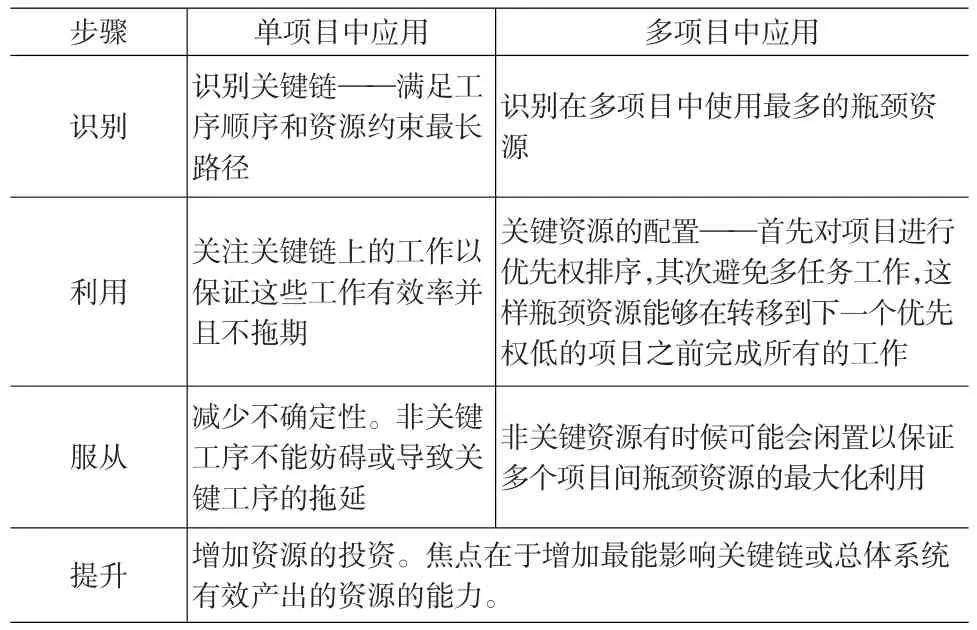
表1 TOC在单项目与多项目应用时的不同[7]

从表1可以看出，关键链方法在单项目和多项目领域的应用有侧重点。Goldratt认为，在多项目环境中，关键的是要关键链用TOC的角度来解决这个问题[1]，核心方法是采用系统的思考，识别系统发展的瓶颈，在各个项目之间协调好资源，尽量减小资源的瓶颈。Goldratt博士提出的关键链多项目管理的步骤如下。

步骤1：设定各个项目的优先权；

步骤2：按关键链方法计划和调度每个项目；

步骤3：交错各个项目，避免资源冲突；

步骤4：设定各项目缓冲及每个项目的输送缓冲；

步骤5：对缓冲区进行有效管理。

虽然提出了以上5个步骤，但是Goldratt对这些骤如何具体实施并没有涉及。现有关于关键链多项目管理的文献也大都基于以上5个步骤进行讨论。

关键链方法在多项目中应用的文献还相对较少，对于瓶颈资源的识别与分配，对于瓶颈缓冲的性质与设置方法还未有统一的、成熟的方法。本论文主要通过对以上问题进行分析，着重对存在较大争议的步骤3——交错各个项目，避免资源冲突进行研究，建立单瓶颈资源约束下的关键链多项目调度模型。

2 瓶颈资源约束下的多项目总收益最大化模型

2.1 问题描述与前提假设

在一个多项目环境中，存在N个相互独立的并行项目，每个项目用Qi表示(i=1,2,3…N）。由于有一种瓶颈资源出现多任务情况，每个项目中仅有一个任务使用，且这些任务发生在关键链上，排除林晶晶（2008）考虑的特殊情况。由于发生瓶颈资源的争夺，因此瓶颈资源在多任务中使用的先后顺序直接影响着不同项目的完工时间。考虑合同交付期的法定效力，瓶颈资源先分配的任务所在项目能够尽快完工，若有提前，将按合同条款给予相应的奖励，后分配到瓶颈资源的任务所在项目可能发生延误，也将按合同条款进行处罚。笔者认为，系统中的重要项目，在发生拖延时，除了造成直接的经济成本上的损失，还会对组织的声誉、战略等造成其他无形的损失。同理，重要项目若能提前完工，除了按照合同规定获取一定的奖励，还会带来额外的收益。所以在建模时考虑利用重要性级数k对成本损失与奖励进行加权，将隐性的损失和奖励量化。

为确定本文分析的背景，需要进行如下假设：

（1）基于约束理论的关键链方法在应用到多项目系统时，要求制约系统绩效的瓶颈资源在使用过程中不间断，以保证资源利用率的最大化。

（2）不考虑项目对其他非瓶颈资源的共享，并假设其他非瓶颈资源的供应量是充分的。

（3）瓶颈资源为可更新的有限离散资源。

（4）不考虑瓶颈资源从一个项目到另一个项目的准备时间；所有资源在工序中的使用一旦开始就不能中断，必须等到工序结束后才能转入其他工序。

（5）瓶颈资源不能通过外部租借或购买等方式获取。

此外，模型中出现各符号的具体指代如下：

Δi为项目i因为瓶颈资源约束造成的延误时间；

index为瓶颈资源在不同项目中的使用顺序的序列；

Pi为前一个使用瓶颈资源的项目编号，其中，Pi=index(j-1),j=2,3,…N；

R为瓶颈资源在每个阶段的可用量；

r为每个瓶颈资源；

Δci为项目Qi每拖延一天的成本损失；

Δei为项目Qi每提前一天完工，所能得到的奖励；

ki为项目Qi的重要性级数，ki越大项目越重要；

Tsi为项目Qi的合同交付期；

Tai为项目Qi的实际完工期；

ti为项目Qi中使用瓶颈资源工序的作业时间。

2.2 瓶颈资源约束下的多项目系统总收益最大化目标模型的建立

基于以上假设和本研究的中心思想，可以建立如下瓶颈资源分配模型

本文所探讨的目标函数是多项目系统总收益的最大化，见式（1），不仅考虑项目实际完成时间与合同交付期的差异造成的奖惩，还考虑不同项目的重要性。为了保证关键链多项目管理思想所提出的瓶颈资源使用的连续性，要求后一个使用瓶颈资源的工序的开始时间等于前一个使用瓶颈资源工序的完成时间，见约束条件（2）。index(j)表示资源分配顺序方案中，第j个分配到瓶颈资源的项目编号，第1个分配到瓶颈资源的项目可以按时完工，不会因资源短缺造成工期延误，因此有约束条件（3）。约束条件（4）说明了瓶颈资源的总量限制。

3 多项目总收益最大化模型的粒子群算法设计

3.1 粒子群算法

粒子群优化（PSO）算法由于其简单性与有效性，在它被提出后不久，就引起了许多研究者的广泛关注，并得到了迅速发展。该算法源于对鸟群觅食等社会行为的模拟研究。作者最初的设想是通过仿真简单的社会系统，研究并解释复杂的社会行为，后来却发现从中可以提炼出一种解决复杂问题的有效优化算法。

PSO算法利用Np个粒子（个体）组成的粒子群在N维问题空间中以迭代的方式搜索最优解。粒子在问题空间中飞行，具有位置与速度两个特征，其中粒子位置对应问题的潜在解。粒子i具有记忆功能，可以记录下自己在飞行过程中曾经历过的最优位置（称为个体最优位置pi）及所有粒子曾经历过的最好位置（称为全体最优位置pg）。每次迭代中，粒子i第j维的速度vij与位置xij按下面的表达式更新

其中，t为迭代次数；i=1,……,Np；j=1,…… N；w为惯性权，c1和c2为加速系数，r1j和r2j为在[0,1]内均匀分布的随机数。式（5）等号右边由3部分组成，第1部分为“惯性”部分，表示粒子保持先前的速度；第2部分是粒子跟踪自己历史最优值的权重系数，表示粒子自身的认识，所以c1又称为认知系数；第3部分是粒子跟踪群体最优值的权重系数，表示粒子对整个群体知识的认识，体现粒子间的信息共享与相互合作。所以c2又称为社会系数。

在PSO算法，粒子速度vi的最大值一般被限制为Vmax。如果粒子第j维的速度绝对值|vij|＞Vmax,j，则该维速度值被限制为Vmax,j，同时保持速度方向不变。粒子位置的第j维xij也被限制在相应的搜索范围[Xmin,j,Xmax,j]。如果粒子在运动过程中，其位置超出了边界，则要进行相应的边界处理[16]。

标准PSO算法步骤如下：

（1）令t=0，初始化种群中粒子的位置xi(0)与速度vi(0)，设定最大速度Vmax与位置边界Xmax，Xmin。初始的粒子个体最优位置pi=xi(0)。

（2）计算每个粒子的适应值f(xi(t))。

（3）更新每个粒子的个体最优位置pi：如果f(xi(t))＜f(pi)，则pi=xi(t)。

（4）更新全体最优位置pg：对于所有的i=1,…,Np，如果f(pi)＜ f(pg)，则pg=pi，g=i。

（5）根据式（1）更新每个粒子的速度。若粒子速度越界，进行越界处理。

（6）根据式（2）更新每个粒子的位置。若粒子位置越界，进行越界处理。

（7）t=t+1，如满足结束条件，算法结束；否则，转（2）。

判断终止条件是设置适应值到达一定的数值或者循环一定的次数。

3.2 利用粒子群算法求解多项目系统总收益最大化目标模型

3.2.1 确定模型的变量

在上述多项目系统总收益最大化目标模型中，要优化的变量为瓶颈资源在各项目中的分配顺序。例如有4个项目，瓶颈资源在这4个项目中分配顺序有24种组合。这些组合称为变量。每种组合x→称为一个个体/粒子。

3.2.2 确定目标函数

调度模型的目标值是最大化项目收益的权重和，它是衡量瓶颈资源调度方案优良情况的标准。在粒子群算法中，粒子的一个位置表示问题的一个解，即资源的一个可行调度方案，每个粒子性能的优劣程度取决于待优化问题目标函数确定的适应值，本文的适应度函数即目标函数为

3.2.3 进化方程设计

PSO中并没有许多需要调节的参数，从现有研究来看，这些参数的经验设置为

粒子群：一般取20～40；

学习因子：c1和c2通常等于2，不过也有其他的取值，但是一般c1=c2，并且范围为[0,4]；

中止条件：设定一定的迭代次数。

3.2.4 收敛条件

收敛性是粒子群算法的一个重要问题，它可以说明这种算法找到的可行解是否最优或者当前找到的解是否满足精度要求。

3.2.5 把实数解转化为整数解

粒子群算法所求出的解是实数形式的，由于本文所讨论问题的特殊性，所要优化的变量是整数，而且是一种排序方式，因此在迭代过程中产生的解可能不合法，就要将不合法的实数解转化为整数解，并把整数列转化为排序的形式，每个值必须而且只能出现一次，步骤如下：

（1）将算法得到组合中的每个数向上取整，比如组合[1,3.4,3.5,2]向上取整后变为[1,4,4,2]；

（2）找出重复的数字。从向上取整后的组合可以看出，组合中有两个4，为重复的数字；

（3）保留不重复的数字，对于重复的数字保留一个，其他的进行替换，将组合中应该出现而未出现的数字替换重复的数字。如向上取整后的组合中，保留1和2，有两个4而未出现3，应该用数字3来替换其中的一个4，替换后的结果为[1,3,4,2]或[1,4,3,2]。

4 算例验证

假设有8个并行项目共享一个单位的瓶颈资源，项目的参数见表2

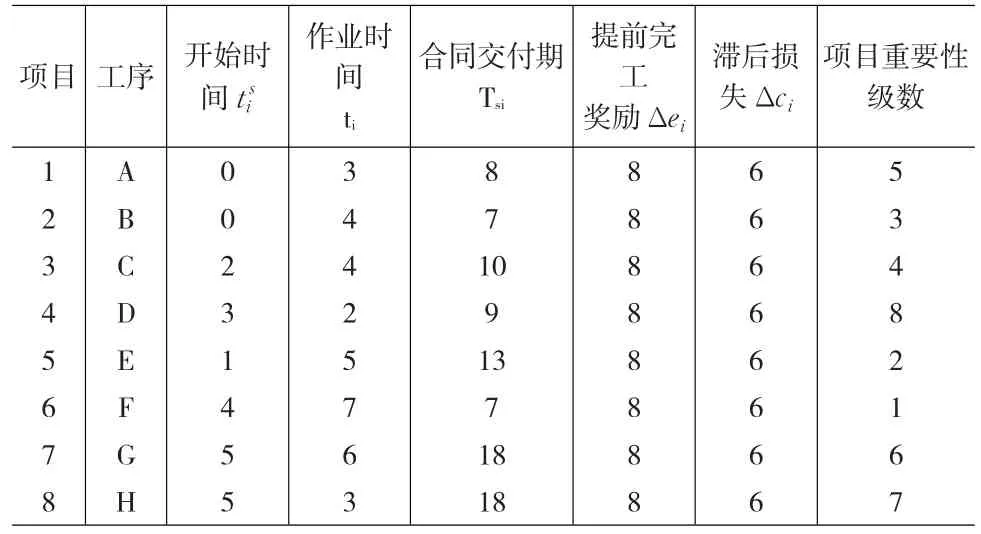
表2 项目参数

我们采用粒子群算法来解决总收益最大化问题，所采用的粒子群算法参数如下：最大迭代代数为100，初始粒子群规模为30，惯性权w=0.55，加速系数c1=c2=2，用Matlab编程语言实现，在硬件环境：CPU：N270 160GHz、内存：1.99GB等和软件环境WindowsXP系统下运行程序。得到的瓶颈资源分配顺序满意解为[2，4，8，1，3，7，5，6]，对应的总收益E=153。

由于粒子群算法的随机性（r1j和r2j为在[0,1]内均匀分布的随机数），每次运行程序所得到的解可能不同，为了检验粒子群算法的收敛性，我们运行程序20次，得到一条平均结果的收敛曲线，见图1。

从图1可以看出，在迭代将近40次的时候已经接近满意解，之后的迭代则为精细搜索，得到的解越来越靠近满意解，这也说明了粒子群算法在解决多项目瓶颈资源分配问题时的有效性。

图1 粒子群算法运行20次得到的收敛图

5 结论

本文详细分析了Goldratt提出的关键链多项目管理5步骤应用法，从定量的角度，在多项目环境中对关键链瓶颈资源约束下考虑多项目总收益最大化目标建立了数学模型，引入粒子群算法解决瓶颈资源在多项目中的分配顺序问题。粒子群算法作为新近出现的一种仿生优化算法，具有随机搜索的优点，且不容易落入局部最优解，并保证了算法的快速性。本文简要地描述粒子群算法的基本概念并给出粒子群算法在关键链多项目进度优化模型中的应用流程，通过算例证明了粒子群算法在解决该问题的可行性、实用性和有效性，为关键链多项目进度优化问题提供了一种新的思路和方法。

需要指出的是，本文解决了单模式下关键链多项目管理中瓶颈资源的分配问题，对于多模式的情况需要进行进一步的讨论研究。

[1]Coldratt E M.Critical Chain[M].New York:the North River Press,1997.

[2]Steyn H.Project Management Applications of the Theory of the Con⁃straints Beyond Critical Chain Scheduling[J].International Journal of Project Management,2002,20(1).

[3]Rabbani M.a,S.M.T.Fatemi Ghomi b,*,F.Jolai a,N.S.Lahiji a.A New Heuristic for Resource-constrained Project Scheduling in Sto⁃chastic Networks Using Critical Chain Concept[J].European Journal of Operational Research,2007,176.

[4]Herroelen WS,Leus R,Demeulemeester EL.Critical Chain Project Scheduling:do not Over Simplify[J].Project Manage Journal,2002,33(4).

[5]Cohen I.,A Mandelbaum,Et al.Multi-Project Scheduling and Con⁃trol:A Process-based Comparative Study of the Critical Chain Meth⁃odology and Some Alternatives[J].Project Management Journal,2004,35(2).

[6]Leach,L.P.Critical Chain Project Management Improves Project Per⁃formance[J].Project Management Journal,1999,30(2).

[7]Lechler,Thomas G.Boaz Ronen,Edward A.Stohr.Critical Chain:A New Project Management Paradigm or Old wine in New Bottles?[J].Engineering Management Journal,2005,17(4).

[8]杨雪松，胡昊.基于关键链方法的多项目管理[J].工业工程与管理，2005,（2）.

[9]郭庆军，赛云秀.关键链多项目进度管理分析[J].西安工业大学学报，2007，27（6）.

[10]马国丰，屠梅曾，史占中.基于TOC的项目管理技术模型[J].系统工程理论方法应用，2005，14（1）.

[11]马国丰，尤建新.关键链项目群进度管理的定量分析[J].系统工程理论与实践，2007，27（9）.