一类Caputo分数阶微分方程边值问题解的存在性
2012-01-05巴哈尔古力
巴哈尔古力,刘 洋
(伊犁师范学院 数学与统计学院,新疆 伊宁 835000)
近年来,分数阶微分方程是研究的热点方向之一,它在材料工程等领域得到了重要的应用.例如:已成功应用于粘弹力学、信号处理、控制等领域.因此研究分数阶微分方程边值问题有着重要的意义.
本文讨论非线性分数分数阶微分方程:

u(0)-u′(0)=0,u(1)+u′(1)=0.

1 基本概念
定义1[1]函数h:(0,)→R的α>0阶Riemann-liouville积分是指:
其中Γ(·)为Gamma函数.
定义2[2-3]函数f:(0,)→R的α>0阶Caputo导数是指:
其中Γ(·)为Gamma函数,n=[α]+1([α]表示小于α的最大整数).

其中ci∈R,i=0,1,2,…,n-1.
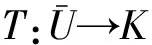
1)T存在一个不动点;
2)存在x∈U,λ∈(0,1) 使得x=λTx.
定理3[6]若u∈C(0,1),且1<α≤2,则分数阶微分方程边值问题:

(1)
u(0)-u′(0)=0,u(1)+u′(1)=0,
(2)
唯一解可以表示为:


根据边值条件(2),可得:

2 主要结果

定义算子T:X→X[7-8]为:

则边值问题(1)有解等价于算子方程Tu=u有不动点.
引理1 若f:[0,1]×R→R是连续函数,则T是全连续算子.
证明易知T是连续的,定义u∈D={u∈X;‖u‖≤l,l>0},

所以,算子T一致有界.下证T等度连续.
∀u∈D,∀ε>0,t1 因此,T是等度连续的,根据Arzela-ascoli定理,算子T是全连续算子. 例1 讨论分数阶微分方程边值问题: 的解的存在性.其中0<θ≤1. 由定理4可以得到: 由定理4知:边值问题存在一个解. [1] Zhang S Q.Existence of solution for a boundary value problem of fractional order[J].Acta Mathematica Scientica,2006,26B:220-228. [2] Bai Z B,Lǘ H S.Positive solutions for boundary value problem of nonlinear fractional differential equation[J].Journal of Mathematical Analysis Applications,2005,311:495-505. [3] J.I.Podlubny.Fractional Differential Equations[M].New York:Academic Press,1999. [4] Tatom F B.The relationship between fraction calculus and fractals[J].Fractals,1995,3:217-229. [5] Moustafa El-Shahed.Existence of a solution for a boundary value problem of fractional order[J].Advances in Applied Mathematical Analysis,2007,2(1):1-8. [6] 郭大钧,孙经先,刘兆理.非线性常微分议程泛函方法[M].济南:山东科学技术出版社,1995. [7] Erbe L H,Hu S and Wang H. Multiple positive solutions of some boundary value problems[J].J Math Anal Appl,1994,184:640-648. [8] Jiang D Q.On the existence of positive solutions to a second order periodic BVP[J].数学物理学报:英文版,1998,18:31-35.

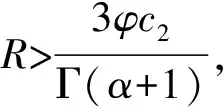
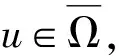
3 例子

