水质扩散系数在伶仃洋水域水体交换中的影响分析＊

方神光

（珠江水利委员会 珠江水利科学研究院，广东 广州510611）

水质扩散系数在伶仃洋水域水体交换中的影响分析＊

方神光

（珠江水利委员会 珠江水利科学研究院，广东 广州510611）

选取珠江河口伶仃洋水域为例，建立了贴体曲线坐标系下的二维珠江河口水流数学模型，并采用纯隐格式的混合有限分析法对数学模型进行了离散和求解。在对模型验证的基础上，针对珠江河口伶仃洋水域中的水质扩散系数选取问题进行了分析和探讨。研究表明，主潮汐通道水体的置换率基本不受扩散系数取值的影响，扩散系数的影响主要体现在远离伶仃洋主潮汐通道和示踪剂浓度分界线的水域，并初步推荐了该水域示踪剂扩散系数的取值范围。

扩散系数；水体交换；伶仃洋；数学模型

（陈 靖 编辑）

珠江口海域是我国近岸污染最严重的海域之一，据不完全统计，每年大量未经处理的生活污水、工业废水直接或间接排入珠江口的污水超过20亿t［1］，大量的污染物日积月累，致使珠江口海域水质普遍超出三类海水水质标准。因此，研究河口水域中的污染物在径潮作用下的输移扩散规律并分析和阐明该海域中海水与外海的交换周期，对珠江河口水域水环境的治理和保护具有重要的指导意义。

海域水体交换是评价海湾的物理自净能力和海湾环境质量的重要指标和手段，是合理开发利用海湾的重要基础。用于海湾水体交换计算和分析的方法主要有：实测资料法、箱型模型法、拉格朗日质点法和对流－扩散型的水体交换法，如PARKER等［2］、高抒等［3］、赵亮等［4］。污染物通过对流输运和稀释扩散等物理过程与周围水体混合，与外海水交换，浓度降低，水质由此得到改善。因此，河口海湾水交换问题的本质是湾内水体在流场中的对流—扩散问题，采用对流—扩散型的数值模型从物理机理上更能反映海湾水交换的本质。但是模型是通过参数化的方法将垂向结构因子的水平扩散作用包纳在水平二维模型中，因此相关参数尤其是扩散系数的选取对模拟的结果影响较大，因为扩散系数的选取不但要能反映水平结构的水动力因子的混合作用，还要能反映上述垂向结构的动力因子对海湾水体混合和弥散的作用。匡国瑞等［5］根据渤海湾实测资料，采用4种滤波方法计算和分析了该海湾的水平和垂直扩散系数，认为湍流扩散系数的选取与时间尺度、潮流特性及选取的计算网格等密切相关；陈时俊等［6］针对水平扩散系数，采用半经验公式给定水深和流速相关的量，对胶州湾污染扩散进行了数值模拟，认为扩散对污染物的输运作用微不足道，潮流输移才是污物向湾口外扩散的主要原因；另外，针对胶州湾的污染物输移扩散问题，郭耀同［7］、吕新刚等［8］和Liu等［9］也先后从潮余流、扩散系数采用温盐同值等不同角度进行了分析和探讨；董礼先等［10］对象山港水交换数值模拟研究中取不同扩散系数得到的水体交换结果表明，当扩散系数取在某一范围内时，最终计算得到的水域水体交换结果相差不大。

为分析不同扩散系数取值对伶仃洋河口水域水体置换计算成果的影响，我们以溶解态保守物质作为湾内水的示踪剂来计算和分析伶仃洋水域的水体交换速率，建立1种基于纯隐格式［11］的对流—扩散型海湾水交换数值模型。先根据实测水文资料对模型进行验证，再对不同扩散系数取值对伶仃洋水域示踪剂浓度输移扩散的影响进行分析和探讨。

1 数学模型及验证

本研究采用正交曲线坐标系下的二维水深平均水动力和水质数学模型①方神光.水流、水质模型软件研究和开发——以港珠澳大桥对珠江口水域的纳潮和水体交换的影响研究为例，2010.；采用纯隐格式－混合有限分析法对该方程进行离散，离散详细步骤可以参见文献［11］。同时此处采用C型网格结合SIMPLER算法用于速度和水位的耦合求解。由于采用曲线规则网格，计算是沿行或列进行，因此计算前首先需要对计算区域的复杂边界进行识别，其相关处理方法以及计算区域存在的浅滩的处理方式可以参见文献［12］。

珠江口水域数模计算范围如图1所示，东西距离约63km，南北距离约145km。整个计算域包括狮子洋、伶仃洋东四口门、香港水道和伶仃洋外万山群岛等。采用贴体正交曲线网格，共布网格436×665个，最大网格尺寸250m×140m，最小网格尺寸30m×8m，图1中的网格给出了局部范围的网格剖分情况。

图1 计算区域及网格剖分图Fig.1 Calculated area and grids

分别选取大、中、小三个潮型对模型进行了验证，用于潮位验证的有12个站点，用于流速和流向验证的有14个站点，此处只给出大潮（2007－08－13T21：00—14T22：00）的部分站点（4个潮位站和4个测流站，如图1所示）验证曲线①，如图2～4所示。从模型验证结果来看，潮位平均误差为9.0cm，流速平均误差为0.17 m/s，流向平均误差为5°。计算的量值和位相均与实测值基本吻合，可真实复演伶仃洋的潮流运动，证明了本研究所用模型的实用性。

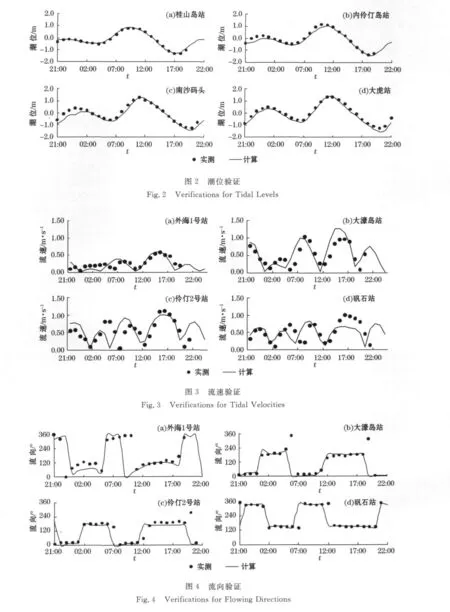
2 水域水体交换计算方法及水体交换边界选取

假定湾内示踪剂的初始浓度为C（t0），湾内水在不同时刻被外海水置换的比率计算公式为

相应余留在原位置未置换的水体比率为

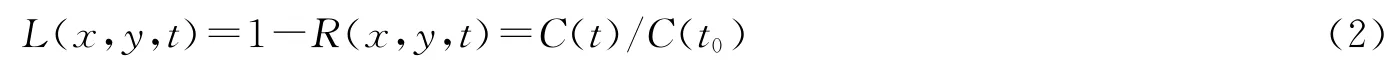
已有研究资料①显示，以内伶仃岛为界，以北区域落潮流速大于涨潮流速，以南区域涨潮流速大于落潮流速；同时根据调查所得污染物中COD的分布区域来看［13］，珠江口伶仃洋水域COD值变化幅度为0.41～2.72mg/L，平均值为1.21mg/L；西北部虎门和蕉门出口一带水域COD值最高，平均为2mg/L；从虎门出口至内伶仃岛之间水域COD平均值为1.5mg/L。从内伶仃岛至伶仃洋出口则逐渐减小，至香港大屿山以西一带水域和河口处桂山岛北侧水域则最低，说明伶仃洋海域COD值由西北向东南水域逐渐递减，且近岸水域值大于远岸值。主要原因是珠江口西北部水域受虎门、蕉门和洪奇沥等径流影响以及沿岸生活污水和工业排污倾废所致。河口东南部一带水域离岸较远，且与南海相通，河口较宽，水交换条件较好，COD值相对较低。因此，根据以上结果，将交换边界设置在赤湾－内伶仃－金星门一线，主要研究不同扩散系数取值对伶仃洋水域水体置换结果的影响（图1）。

3 水质扩散系数影响分析

3.1 计算工况及初始条件和边界条件

1）计算工况

在局部河口海域，水体交换数值模型包括潮流动力模型和溶解态保守性水示踪剂的对流—扩散数学模型。2种数学模型中都存在扩散项和扩散系数，根据相关分析显示［10］，潮流动力模型中的压强梯度力项比扩散项的量级大得多。但扩散项在河口海域内水示踪剂的对流—扩散方程中的情况则大不一样。由于水交换研究需要长时间的模拟计算，扩散项和扩散系数对最后的模拟计算结果的影响较大。鉴于有关珠江河口水域水体交换的扩散系数取值研究成果极为少见，为保证本研究的可靠性，我们分别选取扩散系数为0.1，1.0，10.0和100.0m2/s，即扩散系数每次增为10倍，对2005－01－04T18：00—02－04T23：00期间的水动力和污染物扩散进行了模拟计算。

2）初始条件

水动力模型实际开始计算时间为2005－01－01，在模拟计算4d后的流场趋于稳定，即开始运行保守性物质输运模型。根据上节分析，将赤湾－内伶仃－金星门一线以北水域示踪剂质量浓度场设为1，以南水域设为0，在伶仃洋口门内外水域布置若干取样观察点（图1）。总共模拟30d内珠江河口水域示踪剂浓度的变化情况。

3）边界条件

外海开边界不同时刻的潮位由实测值通过插值方法给定，流速采用二类边界条件，即各时刻边界上的流速值赋值为相邻内部网格点上的计算值；针对模型区域的开边界处的示踪剂，选取进入计算模型区域的外海水示踪物质量浓度为0，流出模型区域的示踪物浓度等同于相邻网格内点（即无梯度），在陆域界处采用无穿透边界条件。

3.2 水质扩散系数的影响分析

分别选取分界线以北水域中的狮子洋1、虎门、蕉门、南沙、西航道1和西航道2六个取样点，分析数学模型中扩散系数选取对水域水体置换的影响。扩散系数分别取0.1，1.0，10.0和100.0m2/s时，各取样点在第5，10，20和30天的计算结果（表1）。分析可见：

1）狮子洋1号取样点在30d后的水体置换率分别为1.2%，1.5%，3.2%和17.1%。表明扩散系数取值越大，得到的狮子洋水体置换率越快；且扩散系数取0.1～10.0m2/s时，模拟计算到狮子洋的水体置换率差别不大，取100.0m2/s时，与前面结果相差较大，同时也说明污染物较难从狮子洋中输运到伶仃洋。

2）虎门取样点第30天时的水体置换率分别为55.1%，58.8%，47.1%和57.4%，相差不大。但在第20天，扩散系数取0.1和1.0m2/s时，水体置换率为51.1%和52.1%，基本一致；取10.0和100.0m2/s时，分别为37.6%和43.1%，可见相差较大。第5天和第10天的变化趋势也基本一致。

3）蕉门取样点第20天的水体置换率分别为16.9%，19.4%，18.2%和36.7%，可见取0.1～10.0m2/s之间时，相差较小。第30天时，水体置换率分别为19.1%，28.5%，35.4%和56.4%，随扩散系数增大，蕉门取样点水体置换率明显增大；且从0.1m2/s增大到10.0m2/s，增为100倍时，该取样点水体置换率增大了16.3%；从10m2/s变化到100m2/s，增为10倍时，该取样点水体置换增大了21.0%；显然扩散系数取0.1～10.0m2/s时，模拟计算到该取样点水体置换率较为接近。

4）南沙取样点第10天的水体置换率分别为7.9%，8.8%，10.6%和21.0%，可见取0.1～10.0m2/s时相差很小；第20天和第30天时，各扩散系数取值下，计算得到的水体置换变化幅度在10.0%以内。

5）扩散系数的变化对伶仃洋主航道上的取样点西航道1和西航道2的水体交换率影响较小。扩散系数分别取0.1和100.0m2/s时，第30天时，西航道1的水体交换率分别为87.6%和83.5%，西航道2的水体交换率分别为99.3%和97.0%；可见伶仃洋主潮汐通道水域水体置换率不受扩散系数取值的影响，且该2取样点水体置换率要远大于其他4个点的值。西航道2取样点由于靠近边界线，该点水体在20d的时间内基本可以完全置换。

靠近示踪剂质量浓度边界线的主潮汐通道水体的置换率基本不受扩散系数取值的影响，扩散系数的影响主要体现在远离伶仃洋主潮汐通道和示踪剂质量浓度分界线的水域，如狮子洋水域和西滩水域（图5～6）。结果表明，质量浓度示踪剂数学模型中的扩散系数取0.1～10.0m2/s时，得到的各取样点水体置换率变化不大。

此处污染物扩散系数取值包含了3个方面的物理含义：1）由本次数学模型中截断误差及离散方法引起的扩散作用；2）包含由于网格尺寸原因而不能模拟更小尺度的涡旋引起的扩散；3）由于二维水深平均数学模型不能模拟垂向弥散而造成的扩散作用。可见，水深平均二维浓度数学模型中的扩散系数取值不再是简单的物理含义，而是各因素综合作用的结果，采用不同的数学模型、离散方法、网格大小及水深地形等，得到扩散系数取值会不同。因此，我们选取的扩散系数取值更多是适应本次研究工况，若移植到其他数学模型或工况则需要进行一定的分析和研究。

3.3 水质扩散系数对伶仃洋各区域水体交换的影响分析

伶仃洋水域水体交换及示踪剂质量浓度的输运和扩散与伶仃洋海域的水动力环境和地形条件密切相关：

1）由于伶仃洋的水深地形呈现“三滩两槽”的格局，潮汐水流主要通过西槽和东槽进入伶仃洋并深入到狮子洋及河网地区，以前的研究表明通过西槽的潮量占伶仃洋纳潮量的85%左右。因此，伶仃洋的主潮汐通道西槽水域水体交换速度要远大于其他水域，潮流输运是水体交换迅速的主要原因，扩散作用可忽略不计。所以低质量浓度水体以西槽轴线为中心呈锲型嵌入虎门口。

2）从东四口门涨落潮时的示踪剂平面质量浓度分布可见：（1）横门水体置换较快主要因为一方面横门距离质量浓度分界线较近，通过金星门进入的新鲜潮水顺着两者间的连通水道很容易直达横门口，另一方面是从其他水域进入横门口水域的示踪剂很少；（2）尽管虎门口门进潮量大，但由于虎门距质量浓度分界线较远，且狮子洋中的高质量浓度示踪剂水体不断通过输运和扩散通过虎门口，对虎门口的水体置换影响很大；（3）蕉门和洪奇沥取样点由于所处位置较为封闭，涨潮水体较难进入，因此水体置换缓慢。

3）伶仃洋西滩水域水体示踪剂质量浓度在落急时显著大于涨急时的值，主要受到洪奇沥和蕉门南支流下泄高浓度示踪剂水体影响较大，但整体来看，由于西滩位置较为开阔，西滩的水体置换优于东滩。东滩水体置换缓慢的原因：（1）伶仃洋东槽潮汐水流的隔离和往复运动，导致伶仃洋东滩水域示踪剂质量浓度不易向外海输移和扩散；（2）从狮子洋经虎门进入矾石水道的高浓度示踪剂水体对东滩水体影响较大。从涨落潮的浓度平面分布可以看出，东滩水域位置的交椅湾、深圳保安机场水域、大铲湾水域的示踪剂质量浓度始终保持在较高值。

总之，模拟金星门－内伶仃岛－赤湾一线以北水域示踪剂质量浓度的输运扩散表明：狮子洋、虎门、蕉门、洪奇沥、东滩和大铲湾水域的水体置换较为缓慢，水质扩散系数的选取会对水体置换的预报存在较大影响；伶仃洋的其他水域如西滩、西槽和东槽水域的水体置换相对较快，水体交换较快的区域同时也是水域开阔及潮汐动力较强的水域，相比之下，扩散作用引起的水体置换几乎可以忽略不计。伶仃洋水域部分站点的水体交换结果见表2。

表2 涨急和落急条件下特征站点的水体置换率（%）Table 2 The rate of water exchange at sampling stations under the conditions of maximal flood and ebb（%）

4 结 论

水质扩散系数的选取对污染物长时间输移和扩散数值模拟计算结果影响较大，我们通过建立珠江河口伶仃洋水域二维水流和水质数学模型，对选取不同扩散系数条件下的水流和污染物输移扩散特性进行了分析和探讨，结果表明：

1）伶仃洋水域质量浓度示踪剂数学模型中的扩散系数取0.1～10.0m2/s时，各取样点水体置换率变化不大。

2）靠近示踪剂质量浓度边界线的主潮汐通道水体的置换率基本不受扩散系数取值的影响，潮汐和径流动力的输运作用占主导地位；扩散系数的影响主要体现在远离伶仃洋主潮汐通道和示踪剂质量浓度分界线的水域，如狮子洋水域和西滩水域。

3）由于水深平均二维水质数学模型中的扩散系数取值不再是简单的物理含义，而是各因素综合作用的结果，建议根据采用的数学模型和网格的具体情况进行调整和使用。

（References）：

［1］KE D S，GUAN Z B，YU H S，et al.Environmental pollution and study trend in Pearl River Estuary［J］.Marine Environmental Science，2007，20（5）：488－491.柯东胜，关志斌，余汉生，等.珠江口海域污染及其研究趋势［J］.海洋环境科学，2007，20（5）：488－491.

［2］PARKER D S，NORRIS D P，NELSON A W.Tidal exchange at Golden Gate［J］.Proc.of ASCE，1972，98（2）：305－323.

［3］GAO S，XIE Q C.Physical model for water exchange process in Xiangshan Bay［J］.Marine Science Bulletin，1991，10（3）：1－9.高抒，谢钦春.狭长形海湾与外海水体交换的一个物理模型［J］.海洋通报，1991，10（3）：1－9.

［4］ZHAO L，WEI H，ZHAO J Z.Numerical study on water exchange in Jiaozhou Bay［J］.Oceanologia Et Limnologia Sinica，2002，33（1）：23－29.赵亮，魏皓，赵建中.胶州湾水交换的数值研究［J］.海洋与湖沼，2002，33（1）：23－29.

［5］KUANG G R，YU G Y，ZHANG H，et al.Calculations of horizontal and vertical diffusion coefficients for field sea［J］.Acta Oceanologica Sincia，1994，16（4）：23－34.匡国瑞，俞光耀，张淮，等.现场海域水平、铅直扩散系数的推算［J］.海洋学报，1994，16（4）：23－34.

［6］CHEN S J，SUN W X，WANG H T.Numerical modeling of of the circulation and the pollutant dispersion in Jiaozhou Bay：II.computation of pollutant dispersion［J］.Journal of Shandong College of Oceanology，1982，12（4）：1－12.陈时俊，孙文心，王化桐.胶州湾环流和污染扩散的数值模拟：Ⅱ.污染浓度的计算［J］.山东海洋学院学报，1982，12（4）：1－12.

［7］GUO Y T.Numerical computation of distribution of COD in Jiaozhou Bay［J］.Transactions of Oceanology and Limnology，1997，（3）：11－17.郭耀同.胶州湾海域COD浓度场数值计算应用研究［J］.海洋湖沼通报，1997，（3）：11－17.

［8］LV X G，ZHAO C，XIA C S，et al.Numerical study of water exchange in the Jiaozhou Bay and the tidal residual currents near the bay mouth［J］.Acta Oceanologica Sincia，2010，32（2）：20－30.吕新刚，赵昌，夏长水，等.胶州湾水交换及湾口潮余流特征的数值研究［J］.海洋学报，2010，32（2）：20－30.

［9］LIU Z，WEI H，LIU G S.Simulation of water exchange in Jiaozhou Bay by average residence time approach［J］.Estuarine Coastal and Shelf Science，2004，61：25－35.

［10］DONG L X，SU J L.Numerical study of the water exchange in the Xiangshangang Bay：I.Advection－diffusion water excange model［J］.Oceanologia Et limnologia Sinica，1999，30（4）：410－415.董礼先，苏纪兰.象山港水交换数值研究：I.对流一扩散型的水交换模式［J］.海洋与湖沼，1999，30（4）：410－415.

［11］LI W.Hybrid finite analytic method for viscous fluid［M］.Beijing：Science Press，2000.李炜.黏性流体的混合有限分析解法［M］.北京：科学出版社，2000.

［12］FANG S G，CHEN C，LIU T.Application of a pure implicit scheme in numerical simulation of coastal tide［J］.Journal of Waterway and Harbor，2008，29（5）：305－309.方神光，陈纯，刘涛.一种纯隐格式在近海潮流数值模拟中的应用［J］.水道港口，2008，29（5）：305－309.

［13］YANG M L，LIN Q，HUANG H H，et al.Distribution feature of COD in the waters of Pearl River Estuary［J］.Marine Science Bulletin，2005，24（4）：22－26.杨美兰，林钦，黄洪辉，等.珠江口水域化学耗氧量（COD）的分布特征［J］.海洋通报，2005，24（4）：22－26.

Analysis of Effect of Water Quality Diffusion Coefficient on Water Exchange in the Lingdingyang Bay

FANG Shen－guang
（PearlRiverHydraulicResearchInstituteofPRWRC，Guangzhou 510611，China）

A two－dimensional mathematical model under the body－fitted curvilinear coordinates was built for the flow in the Lingdingyang Bay of the Zhujiang Estuary and the pure implicit scheme of hybrid finite analytic method was used to discrete and solute the equations.Based on the validation of the mathematical model，the selection of water quality diffusion coefficient values for the Lingdingyang Bay was discussed and analyzed.It is shown that the rate of water exchange within the main tidal channel is basically not affected by the selection of water quality diffusion coefficient values.The influence of the diffusion coefficient emerges mainly in the waters far away from the main tidal channel in the Lingdingyang Bay and from the tracer concentration boundary.The range of the diffusion coefficient values to be selected in the Lingdingyang Bay has been preliminarily recommended.

diffusion coefficient；water exchange；Lingdingyang Bay；mathematical model

January 15，2011

X55

A

1671－6647（2012）02－0177－09

2011－01－15

国家自然科学基金——珠江河口盐水入侵对有机污染物的影响机理研究（51109232）；广东省自然科学基金——珠江河口盐水异重流对有机污染物的影响机理研究（10151061101000001）

方神光（1978－），男，湖北监利人，博士，副研究员，主要从事环境水动力学方面研究.E－mail：fangshenguang＠163.com