Hubbard模型中格林函数的数值计算
2012-01-05朱家昆肖海波舒崧
朱家昆,肖海波,舒崧
(湖北大学物理学与电子技术学院,湖北 武汉 430062)
高温氧化物超导体理论和实验的研究是当今材料科学研究领域的一个热门方向,其所涉及到的物理内涵异常丰富.随着掺杂程度的变化,高温氧化物将展现出反铁磁性、半导导电行为、超导电性、强关联电子系统以及新型金属行为等[1].传统的BCS理论已经无法解释高温氧化物的超导电性,于是在高温氧化物超导体被发现之后的20余年间,出现了众多的理论流派[2-3],尤以Anderson 的非费米液体高温超导理论最为著名,它认为高温超导体的特殊性质是由于组成材料的微观粒子之间的强关联作用引起的,而高温超导体则是一个强关联体系[4].对于该强关联体系,可以用Hubbard模型来描述,Hubbard模型在处理具体的强关联系统当中计算比较复杂,要用到一些数值的方法.本文中主要采用动态平均场论方法结合量子蒙特卡洛模拟(QMC)研究Hubbard模型的数值求解问题.
1 Hubbard模型和动态平均场论
由于高温铜氧化物超导体的超导电性发生于绝缘体-金属相变附近,Anderson认为可用一个近半填充的单带Hubbard模型描述该系统[5]:
(1)
其中niσ=ciσ+ciσ为粒子数算符,ciσ+和ciσ为原子i中电子的产生与湮没算符,σ表示自旋.t=tij(若i、j为最近邻)对应于能带半宽度,U则是格位i上的库仑排斥能(即Hubbard能),μ为化学势.
Hubbard早期工作提出了一个非常接近于Mott初始思想的相变构想,尝试着给出了一个关联系统的能带描述,以氢原子为例,设想有N个氢原子逐渐靠近而排列成晶格,当每个原子只有一个电子时,相当于中性氢原子态H0,当每个原子有两个电子时,电子之间的库仑排斥作用,使它们之间有正的Hubbard能U,这时相当于氢的负离子态H-.若ε0表示第一个电子的能量,ε0+U表示第二个电子的能量.但当氢原子间相互靠近时,能级拓展为能带,分别称为下Hubbard带和上Hubbard带.当相邻原子电子波函数重叠很小时,能带宽度很窄,上、下Hubbard带是分离的,下Hubbard带是满带,上Hubbard带是空带,呈现出绝缘体性质.当原子逐渐靠近,上、下Hubbard带发生交叠,而且都变成部分填充的能带,呈现出金属电导的性质,这种由上、下Hubbard带引起的金属-绝缘体转变,称为Mott转变[6].
这里采用的方法叫做局域掺杂自洽近似(LISA)[7].LISA是Weiss平均场理论在量子多体问题中的自然推广.但是,和普通平均场理论不同的是,在这种方法中并没有假定所有的涨落都被冻结了,确切地说,它冻结了空间涨落却充分考虑了局域量子涨落.所以,LISA方法可以被认为是一种“动态平均场论方法”,在具体计算中,它可以用不同的数值方法来处理,例如精确对角化方法[8]、迭代微扰法[9]和量子蒙特卡洛方法[10-11].本文中主要采用量子蒙特卡洛方法来进行计算.
2 量子蒙特卡洛方法和格林函数的计算
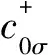

(2)
由有效作用量我们可以得到相应得Weiss有效场函数:
g0(iωn)-1=iωn+μ+G(iωn)-1-R[G(iωn)]
(3)
其中G(iωn)代表着从有效作用量Seff计算而来的格林函数.

(4~5)
R[G(iωn)]可以根据对态密度函数经过一个Hilbert变换所得的函数取反函数而得到其具体形式,而态密度函数对于给定系统,通过计算可以直接给出.设态密度函数为D(ε),则Hilbert变换和其反函数为如下定义:
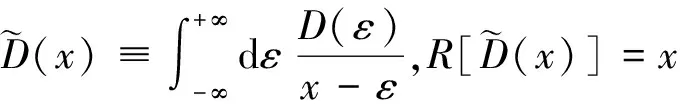
(6)
方程(2~4)构成了一组关于Weiss场函数g0和格林函数G的完备方程组,可以用来自洽的求解格林函数G.
在实际计算中,还可以在动量空间中进行计算.如果在动量空间,格林函数可写为:
(7)

(8)

在一般理论计算当中,格林函数是一个重要的量.如果计算出格林函数G,就可以得到相应的热力学函数,从而进一步去讨论系统的热力学性质.计算格林函数G需要用到不同的数值方法,下面将重点用蒙特卡洛方法来计算格林函数G.
具体计算要采用迭代的方法,其大体思路为:由于格林函数G需要通过有效作用量所给出的Weiss场函数g0来获得,第一步假设g0被给出,通过Hirsch-Fye算法[10]和傅立叶变换(FT)计算出G,还有自能∑;然后它们被自洽的用作条件输入来产生一个新的Weiss场g0.这个过程一直迭代直到得到一个收敛的解(G,g0).
具体迭代步骤如下:
1)先计算出相应的自能:
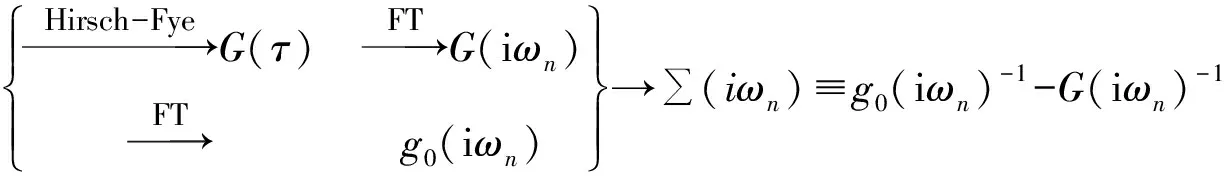
(9)
2)通过Hilbert变换,从上式决定的自能可以得到一个新的格林函数:
(10)
3)从Gnew(iωn)开始,通过傅立叶逆变换(IFT)又可以得到g0new(τ),从而得到一个完整的自洽循环:
(11)
3 数值结果及讨论
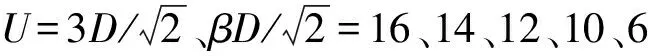

图1 格林函数在反铁磁相下对于不同温度的数值结果
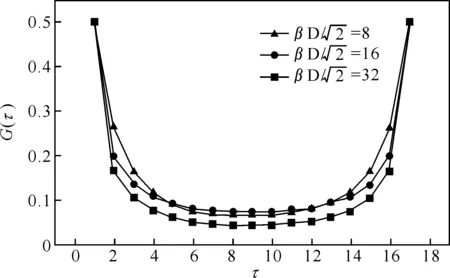
图2 格林函数在顺磁相下对于不同温度的数值结果
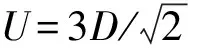
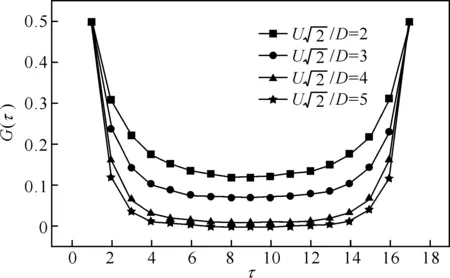
图3 格林函数在顺磁相下对于不同Hubbard能的数值结果

[1] Anderson P W,Schrieffer R. A dialogue on the theory of high Tc[J].Physics Today,1991,44:54.
[2] Schrieffer J R,Wen X G,Zhang S C. Dynamic spin fluctuations and the bag mechanism of high-Tcsuperconductivity[J].Phys Rev,1989,B 39:11663-11679.
[3] Millis A J,Monien H,Pines D. Phenomenological model of nuclear relaxation in the normal state of YBa2Cu3O7[J].Phys Rev,1990,B 42:167-178.
[4] Baskaran G,Zou Z,Anderson P W. The resonating valence bond state and high-Tc superconductivity — a mean field theory[J]. Solid State Commun,1987,63:973-976.
[5] 冯端,金国钧.凝聚态物理学(上卷)[M].北京:高等教育出版社,2002:387.
[6] 黄昆,韩汝琦.固体物理学[M].北京:高等教育出版社,1985:322.
[7] Georges A,Kotliar G,Krauth W,et al. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions[J]. Rev Mod Phys,1996,68:13-125.
[8] Caffarel M,Krauth W. Exact diagonalization approach to correlated fermions in infinite dimensions:Mott transition and superconductivity[J].Phys Rev Lett,1994,72:1545-1548.
[9] Zhang X Y,Rozenberg M J,Kotliar G. Mott transition in thed=∞ Hubbard model at zero temperature[J].Phys Rev Lett,1993,70:1666-1669.
[10] Hirsch J E,Fye R H. Monte Carlo method for magnetic impurities in metals[J].Phys Rev Lett,1986,56:2521-2524.
[11] Georges A,Krauth W. Numerical solution of thed=∞ Hubbard model:evidence for a Mott transition[J].Phys Rev Lett,1992,69:1240-1243.
