具有跨区域的渔业资源的离散动力学模型分析
2012-01-05梁艳顾恩国
梁艳,顾恩国
(中南民族大学数学与统计学学院,湖北 武汉 430074)
随着人口的增长和经济的发展,公共渔业资源的过度捕捞已严重影响其再生能力和人类对它的可持续利用[1].因此再生资源的可持续利用已成为重要的研究课题.众所周知,公共渔业资源的演化是一个复杂的非线性过程,它不仅与资源的自然环境因素(生物种群的自然增长率、生存环境的自然承载能力)有关,还与社会因素有关(市场的价格、捕捞者的捕捞能力和捕捞社会成本)有关.为了更好地掌握全部渔业,需要弄清资源的演化和捕捞情况.为了更好地管理渔业,国际海洋法规把渔业划分为3个区域地分别为:内陆、浅海滩、深海,每部分又以水域差异为主导因素,辅以生产作业和资源特点分为若干区.在国外,关于渔业资源可持续发展的研究很多,关于不同区域生物经济模型也有一些,大多为ODE模型[2-3],早期由Pierre建立的不同的时间刻度下的生物经济连续模型[4],近年来R.Mchich对模型进行了完善,主要研究在多个捕鱼区的捕捞力度的空间分布最优化问题,受到R.Mchich模型[3-5]的启发,考虑到生物种群的数量代与代之间不重叠和捕捞力度是有周期性的,本文中建立离散动力学模型,尽管有人已经提出关于时间演化的渔业资源离散动力模型,但没有考虑鱼与渔船在不同区域的游动的速度和鱼和船只的增长速度差别,因此,本文中在假设有两种时间刻度的基础上,建立一个跨区域的渔业资源和捕捞力度的时间演化的离散动力模型,用聚合方法简化成二维的动力系统,先分析正不动点的存在性和局部稳定性,再分析可行域的边界即当前渔业资源在什么范围才能保持不枯竭.
1 模型的建立
主要考虑3个毗连的渔业区域,并且在t时刻鱼的密度分别为x1(t)、x2(t)、x3(t),捕捞力度分别为E1(t)、E2(t)、E3(t),为了便于分析,我们假设所有的渔船出海时间是相同的,这样每个区域的捕捞力度可用船队拥有的船只数量来测量.
假设存在两个不同的时间刻度,在快的时间刻度(一秒)下,资源的总储量和船只的总数目被假设为保持不变.因此,这个模型此时仅描述鱼与船只在不同区域的变化,在慢的时间刻度(一年或一个季度或一月),鱼的总储量和船只的数目发生了变化.在每个区域的渔业资源和捕捞力度的演化模型由Barbier[5]提出.对于鱼的储量,用logistic模型描述鱼的增长随着捕获而减少,即
xi(t+1)-xi(t)=rixi(t)(1-xi(t)/Ki)-h(xi(t),Ei(t)),
这里ri和Ki(i=1,2,3)分别表示第i个区域自然增长率和环境承载能力.对于捕捞力度而言,捕捞船只的增加或减少要随渔民收益而变化,即
Ei(t+1)-Ei(t)=ph(xi(t),Ei(t))-ciEi(t),
这里ci是第i个船队的捕捞成本,p是鱼的市场价格.根据前面的假设,建立系统如下:
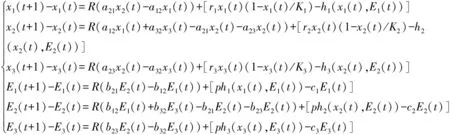
(1)
h(xi(t),Ei(t))=qiEi(t)xi(t)(i=1,2,3),qi为个体i的捕捞能力,aij表示鱼从区域i到区域j的迁移率,bij表示渔船从区域i到区域j的迁移率,R>>1是鱼和船(每年或每个季节或每个月)迁移的次数,假如令ε=1/R,方程(1)可以被写成下列形式:
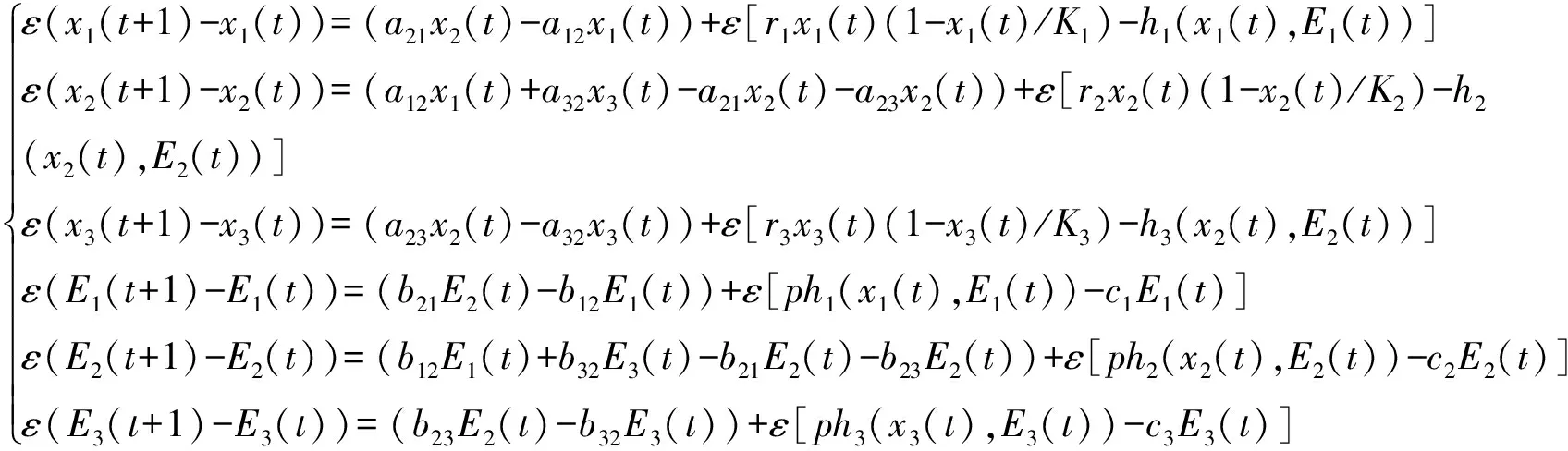
(2)
令x(t)=x1(t)+x2(t)+x3(t),E(t)=E1(t)+E2(t)+E3(t),ε=0其中xi=αix,Ei=βiE(i=1,2,3),
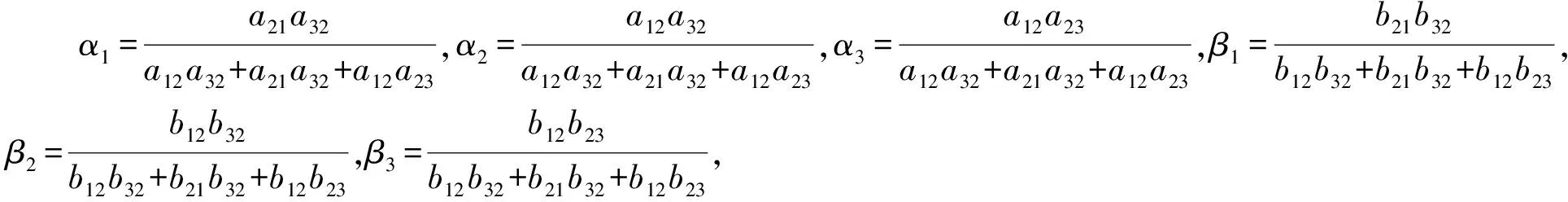
(3)
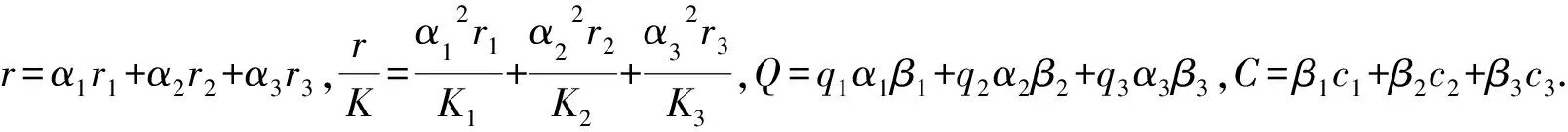
2 非负平衡点的存在性
(3)式可以写成映射动力系统形式:
(4)
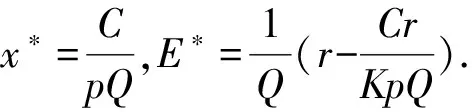
3 非负平衡点的局部稳定性和分叉
为了得出系统(4)的平衡点稳定性,我们考虑系统(4)的Jacobian矩阵:
(I)在E0(0,0)处,有

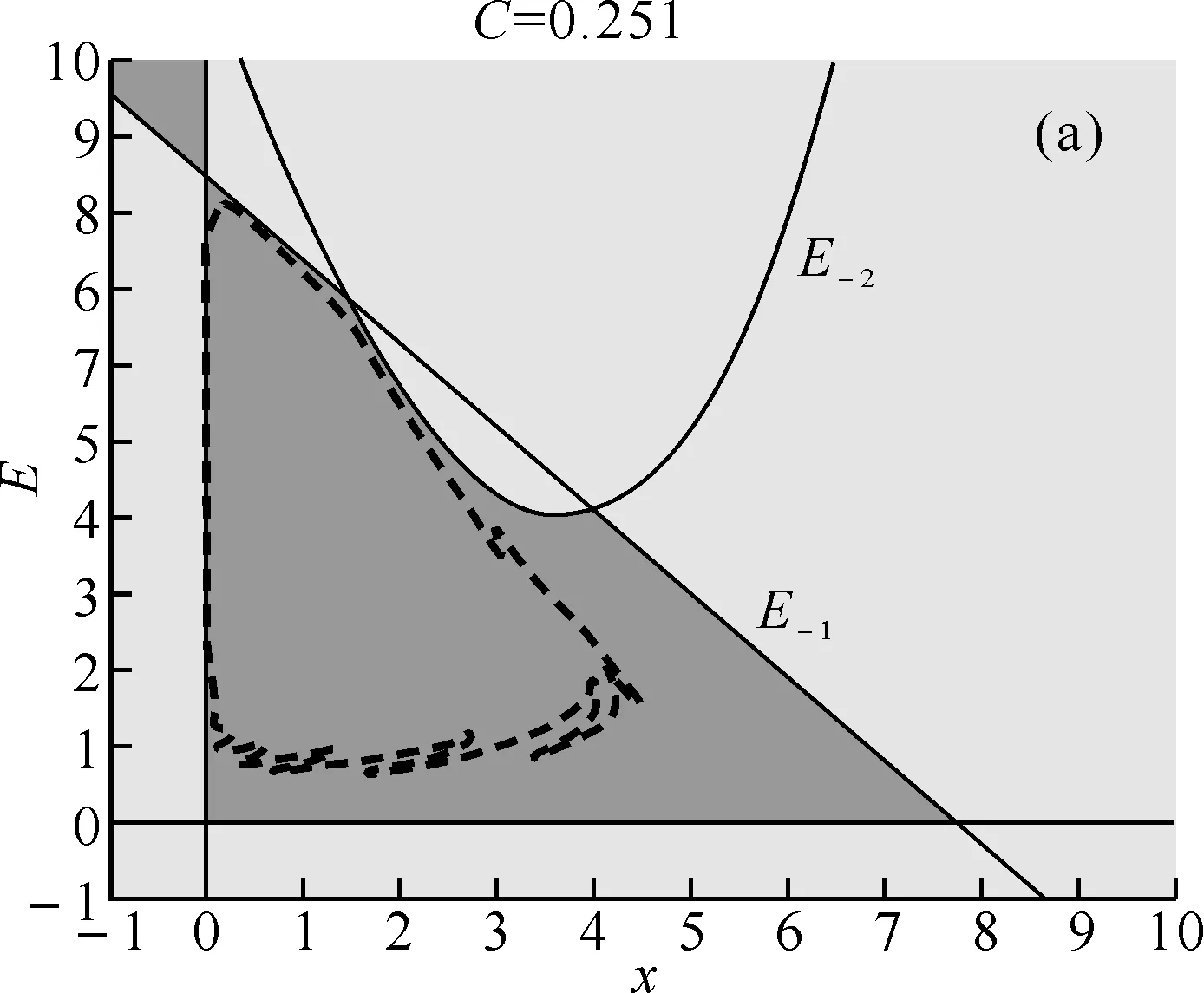
可得到平衡点E0, 当0 (II)在E1(K,0)处,有 当0 (III)在P(x*,E*)处,我们有 其矩阵的特征多项式为 P(λ)=λ2-tr(J)λ+det(J), 由Jury条件p(1)=1-tr(J*)+det(J*)>0,P(-1)=1-tr(J*)+det(J*)>0,1-detJ*>0时,关于正平衡点p的稳定性我们有下面定理. 定理1 (2)当C=C1=KpQ时,系统(4)发生跨临界分叉.当C>C1时正平衡点p(x*,E*)失去稳定,E1(K,0)开始稳定;当C (4)当C=C3=KpQ-1时,系统(4)在p(x*,E*)处产生Neimark分叉;当C 图 1 系统(4)关于参数K=5,r=11/6,p=1,Q=1/3随着参数C变化的可行域 次迭代为负,因此在第一象限并且在直线X-1左边的点属于不可行吸引域,可行域边界此时完全由坐标轴和X的前像构成,如图1(d);从图1(a)中,我们可以看到混沌吸引子与可行域的边界很接近,在这种情况下,外部环境一个很小的扰动都会导致资源的灭绝. 本文中提出的是跨边界的渔业资源的离散动力学模型,对模型进行非线性分析,得到正平衡态的存在性和局部稳定性,并从全局上分析了可行吸引域的结构,从而揭示了渔业资源可持续利用的内在规律。在这篇文章里,我们只简单地考虑了3个区域,然而,这种方法对渔业区域研究可简单地推广到N(N>3)个,还有,在文中,我们把鱼的市场价格假设为常数,在短期内是可行的。事实上,它应是一个变量,主要取决于市场需求和供应的差异,有待以后研究. [1] Garcia,Grainger J R.Gloom et al. The future of marine capture fisheries[J].Philosophical Tanscations of the Royal Society, 2005,B360:21-24. [2] Mchich R,Auger P M,Bravo de la parra R, et al. Dynamics of a fishery on two fishing zones with fish stock dependent migrations:aggregation and control[J].Ecol Model,2002,158: 51-62. [3] Mchich R,Charouki N,Auger P M,et al. Optimal spatial distribution of the fishing effort in a multi fishing zone mode[J]. Ecol Model, 2006,197:274-280. [4] Pierre Auger, Rachid Mchich, Nadia Raissi,et al. Effects of market price on the dynamics of a spatial fishery model: over-exploited fishery/traditional fishery[J]. Ecol Model, 2010,7(1): 13-20. [5] Barbier E B,Strand I,Sathirathai S.Do open access conditions affect the valuation of an externality?Estimating the welfare effects of mangrove-fishery linkages[J].Env Resour Econ,2002,21:343-367. [6] Gu Enguo.Global bifurcations of domains of feasible trajectories: analysis of a predator-prey model[J].Int J of Bifurcation and Chaos,2006,16(8):2601-2613.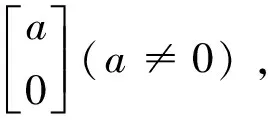
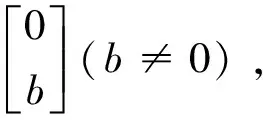
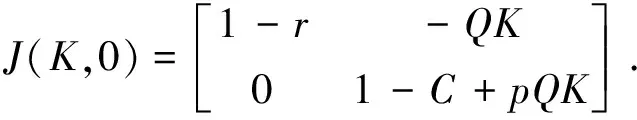


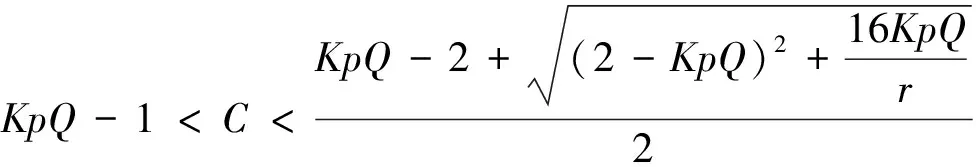

4 正平衡点的全局分析
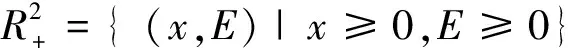
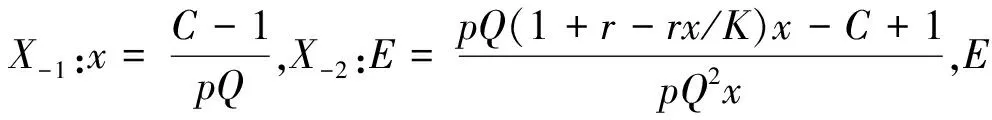
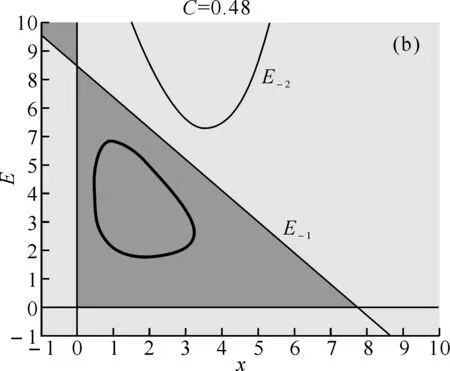
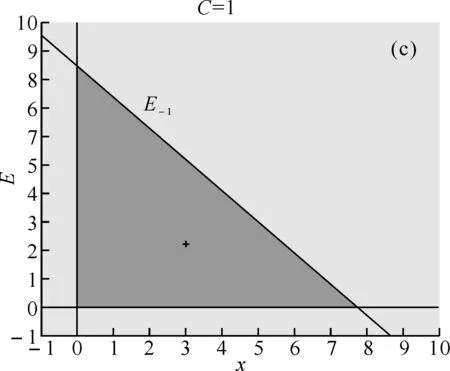
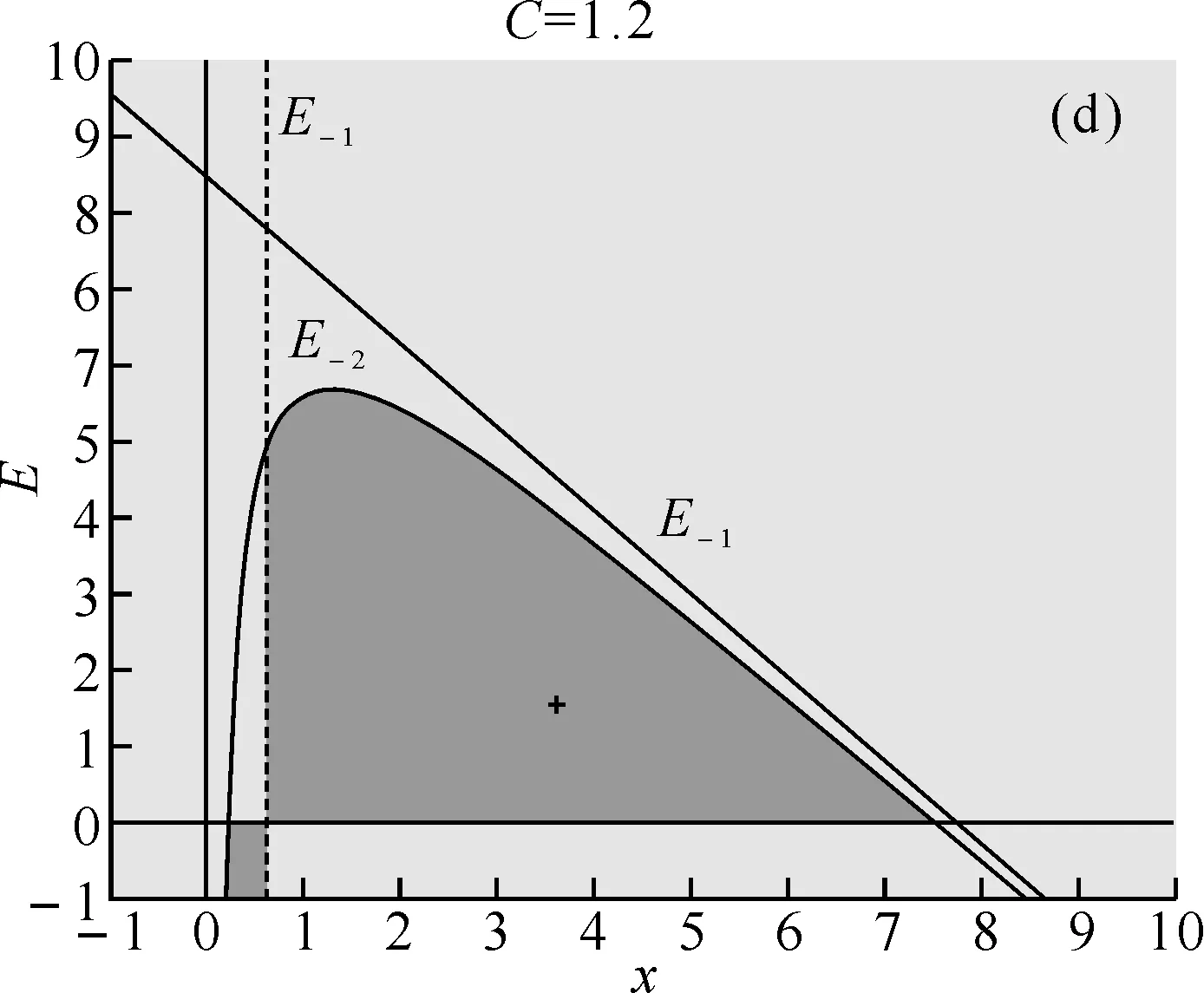
5 结语
