Stokes问题的Galerkin-Hermite小波方法

陈一鸣， 汪晓娟， 杨 莹， 陈 娟

(1.燕山大学 理学院 河北 秦皇岛 066004；2.中国矿业大学 理学院 江苏 徐州 221116)

0 引言

Stokes问题是流体力学中最简单的数学模型，描述黏性不可压流体的流动,文献[1]研究了它在典型域上的情形，得到了典型域上的自然积分方程.文献[2]对此作了进一步研究，推出强奇异积分的计算方法，采用与区域形状相关的Green函数形成的自然边界元法计算了圆内区域Stokes问题，但并未得到刚度矩阵的计算公式.祝家麟[3]从速度—压力公式出发，利用单层位势表示定常Stokes 方程Dirichlet 问题的解，用Galerkin 边界元法求解,但编程和计算都很繁琐.

近10年来，小波分析被广泛应用于偏微分方程和积分方程数值解[4-7].目前,与方程有关的各种类型的区域上的小波研究已有了许多成果,但构造区域上性质好的小波基仍然是一个非常重要的研究领域.本文将Galerkin-Hermite小波方法应用于圆内区域的Stokes问题,得到了简便的刚度矩阵计算公式，对一个2J+3×2J+3阶的刚度矩阵，仅需计算其中2J+3J+7个元素,大大降低了计算量.

1 Stokes问题自然边界归化[2,8]

设Ω为单位圆，其边界Γ，考察式(1)的第二边值问题，

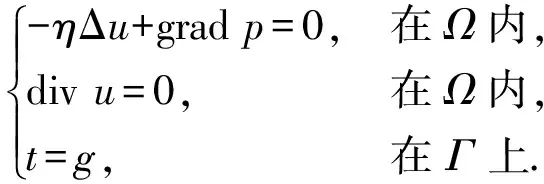
(1)

由直角坐标变换，易得关于半径R的圆内区域Ω的Stokes问题的Poisson积分公式：

(2)

Stokes问题(1)式相应的自然积分方程为

Ku0=g,

(3)

定义连续双线性和连续线性泛涵：

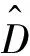
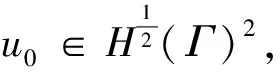
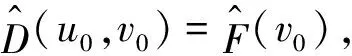
(4)

2 Hermite插值小波[9]

定义1若尺度函数

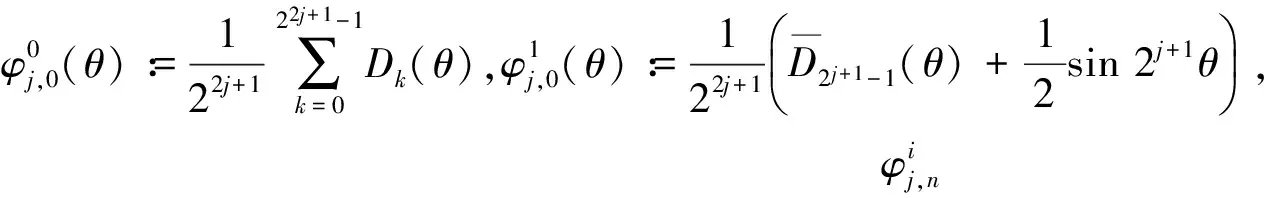
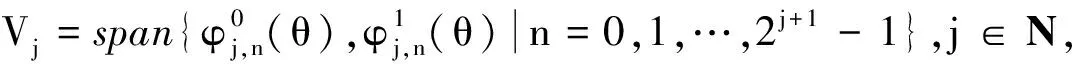
定义2若小波函数

且当j∈N,n=1,…,2j+1-1时，

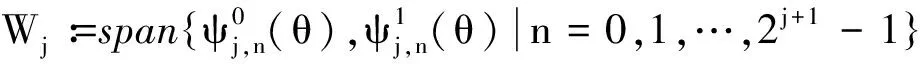
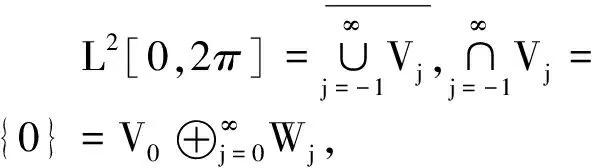
3 数值离散化

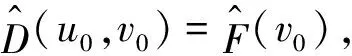
(5)

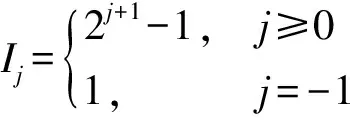
(6)

这里，p,q=0，1,-1≤j,j′≤J-1,0≤k≤Ij，0≤k′≤Ij′.

以及(b1,b2,…,bk)表示由{b1,b2,…,bk}产生的循环矩阵，则有

证明先计算矩阵A11的元素：

(i)当0≤j,j′≤J-1时，

利用Hermite小波的性质，直接积分计算，得：

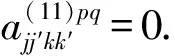
(b)当p=q=0时，有I=0,且

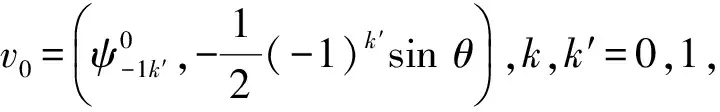
综上，类推可得定理2.

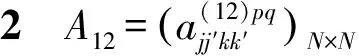
4 数值算例

将利用上述方法求解圆内Stokes问题第二边值问题的数值解，设η=1.

例单位圆内第二边值问题：

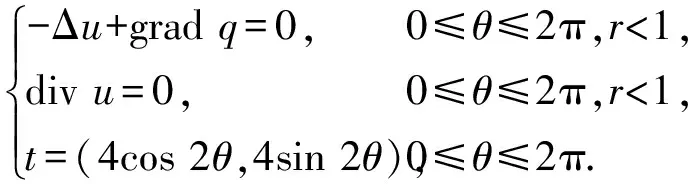
该问题的准确解是：u(r,θ)=(r2cos 2θ,r2sin 2θ),q(r,θ)=-8rcosθ,利用Hermite三角小波解它等价的自然边界元方程对应的变分问题，若取J=0,则

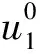
它也等于该问题的准确解，则能量模估计及L2估计皆等于0.

定理1及定理2整个矩阵的计算及数值算例表明，由于很好利用了Hermite三角小波的性质，使得矩阵元素的计算量大大减少,无需编程和繁琐的计算,较文献[3]简便,同时也避免了用有限元方法[10-11]求解中存在的构造混合元格式时自由度大、结构复杂等问题,充分利用了矩阵块元素的对称性、循环性、稀疏性,给数值解Stokes问题带来了很大便利,节省了存储空间。

[1] Feng Kang，Yu Dehao．Cannonical integral equations of elliptic boundary value problems and their numerical solutions[C]// Proceedings of China-France Symposium on the Finite Element Method.Beijing,1983: 221-252．

[2] 余德浩.自然边界元方法的数学理论[M]．北京: 科学出版社,1993: 359-441．

[3] 祝家麟.平面定常Stokes问题的Galerkin线性边界元解法[D].重庆: 重庆大学,2005.

[4] Glowinski R,Lawton W,Ravachol M,et al.Wavelets solution of linear and nonlinear elliptic,parabolic and hyper-bolic problems in one space dimension[C]//Computing Methods in Applied Sciences and Engineering,Proc 9th Int Conf.Paris ,1990: 55-120.

[5] Wells R O Jr,Zhon X.Wavelet solutions for the Dirichlet problem[J].Numer Math,1995(70): 379-396.

[6] Chen Wensheng,Lin Wei.Hadamard singular integral equations and its Hermite wavelet methods[C]//Proceedings of the 15th International Colloquium on Finite or Infinite Dimensional Complex Analysis.Beijing,1997: 13-22.

[7] 王先标,林伟.Hammerstein积分方程的ID小波方法[J].计算数学杂志,1998,16(6): 499-508.

[8] Chen Wensheng.Galerkin-Shannon wavelet methods for the stokes problem[J].Journal of Shenzhen Univerdity Science and Engineering,2001,18(1): 33-38.

[9] Quak E.Trigonometric wavelets for Hermite interpolation[J].Math Comput,1996,65 (214): 638-722.

[10] 杨永琴,肖留超.Stokes问题的一个非协调有限元逼近[J].广西师范大学学报:自然科学版，2008,26(2): 49-52.

[11] 陈绍春,肖留超.Stokes问题的非协调有限元逼近[J].郑州大学学报：理学版，2005,37(2): 20-23.