带干扰的多险种二项风险模型的破产概率

刘 超， 王永茂， 颜 玲， 吴琳琳， 王怡菲

(燕山大学 理学院 河北 秦皇岛 066004)

0 引言

经典风险模型及其推广模型[1-2]均描述的是单一险种风险过程.但在实际中,由于保险公司业务种类的日益多元化,经典的风险模型已经不能很好地描述现实过程.因此,讨论多险种风险模型更具实际意义.

文献[3]将保单到达过程进行了推广，讨论了广义复合二项风险模型下的生存概率；文献[4-5]讨论了双险种风险模型的破产概率，文献[6]则在其基础上讨论了带干扰的风险模型的破产概率.为了更好描述保险公司业务种类的多元化，本文研究了多险种的风险模型.

1 模型建立

设

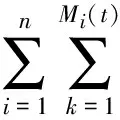
(1)

其中,U(t)为盈余过程，u≥0为初始资金，τ≥0为投资利率，ξ≥0为通货膨胀率，{S(t),t≥0}表示保险公司在时刻t的盈利部分，称为盈利过程.这里所用到的随机变量都定义在完备概率空间(Ω,F,P),t≥0上.

1){Mi(t),t≥0}，i=1,…，n,表示第i个险种在时间(0,t)内收取的保费次数，它是以pi，i=1,…,n为参数的二项随机序列，Mi(0)=0，i=1,…,n，并且相互独立.

2){Nj(t),t≥0},j=1,…,n表示第j个险种在时间(0,t)内索赔的次数，它是以μj，j=1,…,n为参数的二项随机序列，Nj(0)=0，j=1,…,n，并且相互独立.

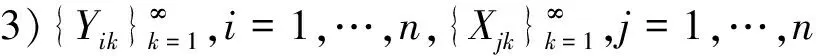
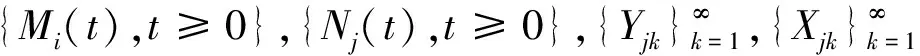
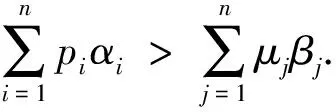
T=min{t|t≥0,U(t)<0}，表示破产发生的时刻，最终破产概率有Ψ(u)=p{T<∞|U(0)=u}.

模型(1)包括了一些学者讨论的情形.

当n=1时，模型(1)为带干扰的单险种风险模型，即

当n=2时，模型(1)为带干扰的双险种风险模型，即

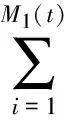
2 盈利过程{S(t),t≥0}的性质

性质1{S(t),t≥0}具有平稳独立的增量.

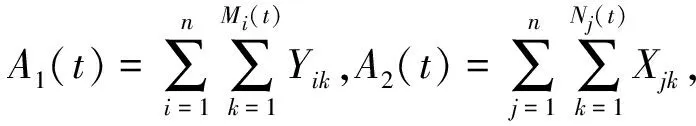
S(ti)-S(ti-1)=[A1(ti)-A1(ti-1)]-[A2(ti)-A2(ti-1)]+a[W(ti)-W(ti-1)],

由于A1(ti)-A1(ti-1),A2(ti)-A2(ti-1),W(ti)-W(ti-1)，i=1,…,n,是相互独立的，所以盈利过程{S(t),t≥0}具有独立的增量.又因为

S(t+j)-S(t)=[A1(t+j)-A1(t)]-[A2(t+j)-A2(t)]+a[W(t+j)-W(t)]

对一切t≥0,A1(t+j)-A1(t),A2(t+j)-A2(t),W(t+j)-W(t)分别具有相同的分布，所以对一切t≥0,S(t+j)-S(t)也具有相同的分布.即{S(t),t≥0}具有平稳的增量.因此盈余过程{S(t),t≥0}具有平稳独立的增量.

性质2

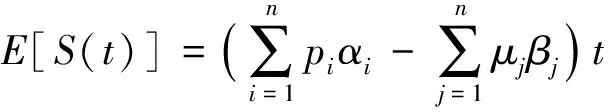
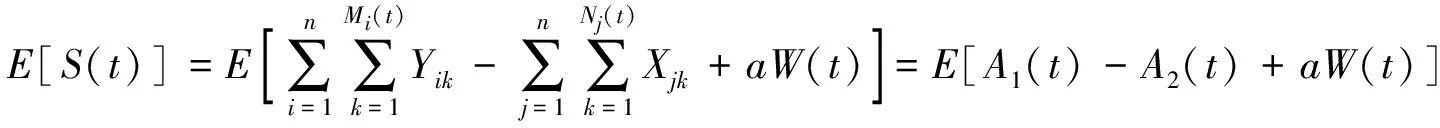
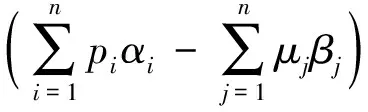
又因为随机过程{Mi(t),t≥0},i=1,…,n,{Nj(t),t≥0},j=1,…,n，{W(t),t≥0}相互独立,

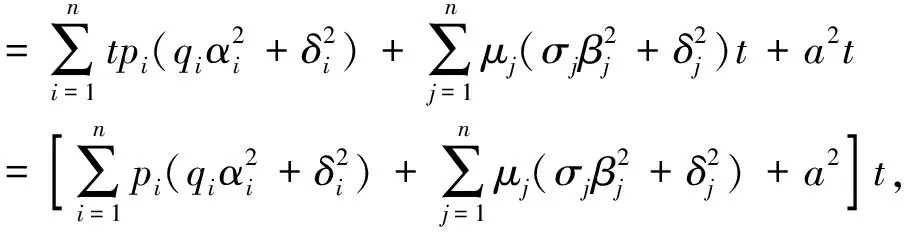
其中qi=1-pi,μj=1-σj,i,j=1,…,n.

3 破产概率

定理1存在函数g(r)使得E[e-rS(t)]=etg(r).

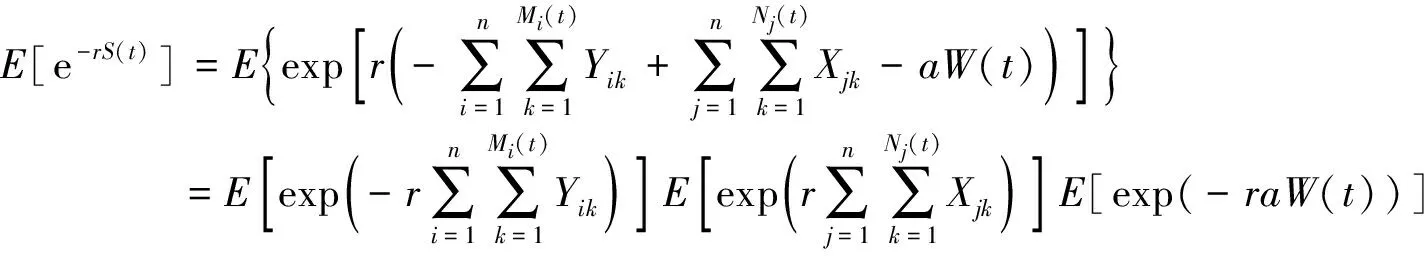
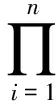
其中MYi(-r)=E[e-rYi]为险种i保费收入的矩母函数，MXj(r)=E[erXj]为险种j理赔额的矩母函数.

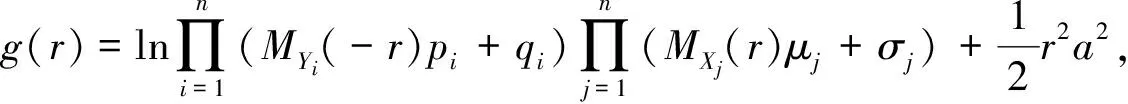
定理2方程g(r)存在唯一正根r=R，称R为调节系数.

证明因为保费和理赔额相互独立，且二阶矩存在.所以

有

故曲线g(r)是下凸的.方程至多有两个解，显然g(0)=0,r=0是平凡解，又因为g′(0)<0，且当r→∞时，g(r)→+∞，因此存在唯一R∈(0,+∞)，使g(R)=0，即方程g(r)=0在r>0时有唯一正根R.

定理3在由(1)式建立的风险模型{U(t);t≥0}下，最终破产概率为

证明对于任意的t>0,r>0有

E[e-rU(t)]=E[e-rU(t)|T≤t]p{T≤t}+E[e-rU(t)|T>t]p{T>t}

,

(2)

由于E[e-rU(t)]=E[e-ru(1+τ-ξ)]E[e-rS(t)]=e-ru(1+τ-ξ)etg(r),当r=R时，g(R)=0,所以E[e-RU(t)]=e-Ru(1+τ-ξ),代入(2)得

e-Ru(1+τ-ξ)=E[e-RU(t)|T≤t]p{T≤t}+E[e-RU(t)|T>t]p{T>t}.

当T≤t时，令

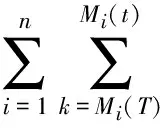
因此

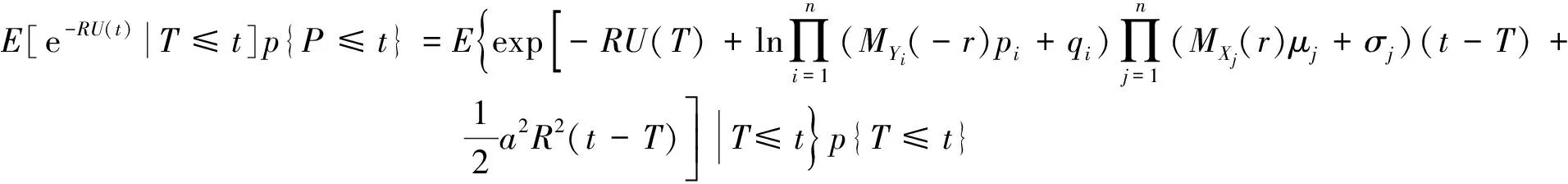
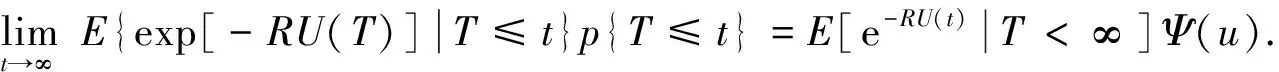
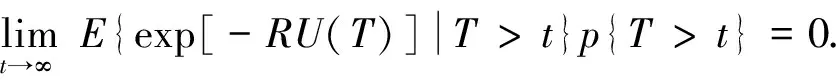
事实上，

令

因ω>0，在t充分大时，Q(t)>0.

因此

E{ exp[-RU(T)]|T>t}p{T>t}

=E{exp[-RU(T)]|T>t,0≤U(t)≤Q(t)}p{T>t,0≤U(t)≤Q(t)}+
E{exp[-RU(T)]|T>t,U(t)>Q(t)}p{T>t,U(t)>Q(t)}

≤p{0≤U(t)≤Q(t)}+exp(-RQ(t)),

由契比雪夫不等式得

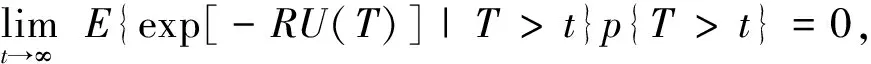
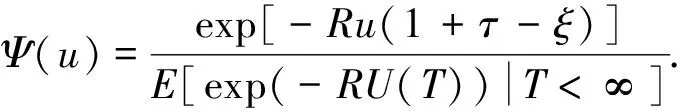
推论在(1)式风险模型{U(t),t≥0}下，最终破产概率Ψ(u)满足Lundberg不等式

Ψ(u)≤e-Ru(1+τ-ξ),

此式给出了最终破产概率的上界.

[1] 谢志刚，韩天雄.风险理论与寿险精算[M].天津：南开大学出版社,2000:101-189.

[2] Gerber H U.An Introduction to Mathematical Risk Theory[M].Philadelphia:Homewood,1979.

[3] 龚日朝，刘永清．广义复合二项风险模型下的生存概率[J]．湘潭大学学报：自然科学版，2001,23(2)：15-19.

[4] 蒋志明，王汉兴.一类多险种风险过程的破产概率[J].应用数学与计算数学学报，2000，14(1): 52-62.

[5] 刘东海，刘再明.双险种二项风险模型的破产概率[J].华东交通大学学报，2005，22(5)：162-166.

[6] 张相虎，赵明清.带干扰的双二项风险模型的破产概率[J].经济数学，2005，22(4)：351-355.