随机环境马氏链下弱遍历性及其应用

宁小青，郭光耀

(武汉工程大学 理学院，湖北 武汉 430073)

1 弱遍历性

x与y相遇示意图

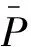
定义1 称p-θ链是弱遍历的，如果对任意x,y∈X，δ(x,y,θ)=0.

可见，弱遍历性描述了一种无记忆性，即经过很长的一段时间后，初始状态的影响将不再存在.这种定义是与经典马氏链的理论相一致，参见文献[1-6],本文首先介绍相遇关系，然后利用相遇关系讨论弱遍历性，并研究弱遍历性在经济学中的应用.

2 相遇关系

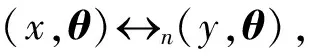
(x,θ)与(y,θ)相遇的直观含义是指从两个不同的初始状态x,y出发，在相同的环境下，经有限步后，会相遇在同一状态的概率大于0.

证明设(x,θ)与(y,θ)相遇，则存在n≥1使得：S(x,θ,n)∩S(y,θ,n)≠φ，即∃z∈X，满足p(n)(θ;x,z)>0，p(n)(θ;y,z)>0，故∀l∈S(z,Tnθ,k)，

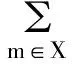
由z∈S(x,θ,n),l∈S(z,Tnθ,k)，得p(n+k)(θ;x,l)>0，故l∈S(x,Tn+kθ,n+k)，仿之可证l∈S(y,Tn+kθ,n+k),结论成立.

定理2 假设(x,θ)与(y,θ)相遇，则δ(x,y,θ)<2.

证明设(x,θ)与(y,θ)相遇，则存在n≥1使得S(x,θ,n)∩S(y,θ,n)≠φ，即∃z∈X，满足p(n)(θ;x,z)>0，p(n)(θ;y,z)>0.将X划分为3个部分：

Z1={z:p(n)(θ;x,z)>0,p(n)(θ;y,z)>0}

Z2={z:p(n)(θ;x,z)>0,p(n)(θ;y,z)=0}

Z3={z:p(n)(θ;x,z)=0,p(n)(θ;y,z)>0}

则有：

由p(n)(θ;x,z)>0，p(n)(θ;y,z)>0，可得：

δn(x,y,θ)<∑z∈Xp(n)(θ;x,z)+∑z∈Xp(n)(θ;y,z)=2

又因为δn(x,y,θ)非增，所以δ(x,y,θ)<2.反之，若δ(x,y,θ)<2，则一定存在n使得δn(x,y,θ)<2，而上面的推导步步可逆，所以结论成立.

定理3 设M为最大不变测度的支撑，则对∏a.e.(x,θ)∈M和所有的y,z∈S(x,θ,n)，有：

δ(y,z,Tnθ)<2.

证明设φ为最大不变测度的密度，则M=(φ>0)，令:

如果y∈S(x,θ,n)，那么:

S(y,Tnθ,k)⊂S(x,θ,n+k)，

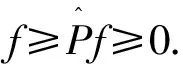
f(x,c)>f(y,Tnθ)+f(z,Tnθ).

由于f是εi可测，则f(x,θ)=0.

定理4 令C1={(x,θ)∈C:δ(y,z,Tnθ)<2,y,z∈S(x,θ,n),n≥1}，则C1为封闭集，且把过程限制在C1上时，↔为等价关系.

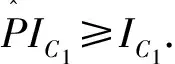
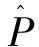
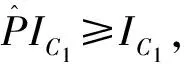
因为∀u,v∈S(y,Tθ,n)有：

p(n)(Tθ;y,v)>0，p(n)(Tθ;y,u)>0，

所以p(n+1)(θ;x,v)>0，p(n+1)(θ;x,u)>0.于是，u,v∈S(x,θ,n+1)，因为(x,θ)∈C1，从而δ(u,v,Tn+1θ)<2，也即(y,Tθ)∈C1.故C1为封闭集.

u∈S(x;θ,l)∩S(y;θ,l)，v∈S(y;θ,l)∩S(z;θ,l).

由于u,v∈S(y,θ,l)，故有δ(u,v,Tlθ)<2.所以(u,Tlθ)，(v,Tlθ)相遇，从而(x,θ)与(z,θ)相遇.因此定理得证.

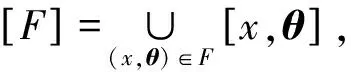
定理5 设π是遍历的,E=M,μi={Φ},Λ(M)=1,令φ为Φ的密度函数，有：

证明对α∈P(X)，由定理的假设和文献[5]定理5.2.1可得：

δ(α，φ(·，θ)，θ)=0，π.a.e.

对任意ε>0，由Birkhoff遍历定理及上式可知，存在正整数Nε使得:

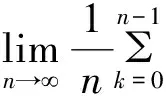
在等式右边用δk代替δN,0≤k≤n-1.由定理2得δk非增，所以对k≥N有：

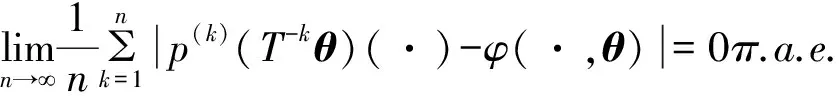
3 在管理学方面的应用

下面利用随机环境的马氏链的相遇关系来研究管理学方面的人员配备问题，假设某汽车出租公司有l个不同的服务网点，负责汽车租车与还车业务，顾客可以在任意网点租车与还车，开始时各网点的汽车数量不妨设为(n1,n2,…,nl)，现在公司要根据各网点的汽车数量决定安排服务人员的人数，本文研究经过一定的时间后，各网点人员配备是否达到一定的稳定状态.

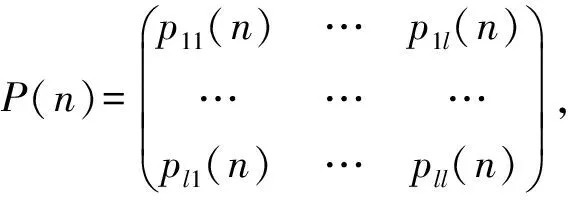
首先，由于l有限，并且在第x个网点租车的顾客在单位时间后可以任意在第y网点还车，则存在ε>0，使π(θ:L(x,θ;[E]y)>ε)=1，即状态间一致互通，则由文献[7]定理2，一定存在状态x是弱常返的，即G((x,θ);[E]x)=，也即), 而由于y有限，则：

进一步的，并且在第x个网点租车的顾客在单位时间后可以任意在第y网点还车，则对于任意状态x,y，也即两个不同的网点x,y，总存在一个状态z，也即一个网点z，顾客在两个不同的网点x,y租车一段时间n后一定可能会同时在z网点还车，由此可知，状态x,y会相遇于z，由定理1，n以后时间后x,y也相遇，故如果按相遇关系分类，Λ(M)=1，即只有一个相遇类，从而由顾客租车与还车而构成了一个随机环境的马氏链，满足定理5的所有条件，则：

成立，

从直观上讲，经过长时间的汽车出租，各网点汽车数量的比例会达到稳定的φ(·，θ).从而可以根据φ(·，θ)来安排个网点的服务人员的人数.

明显地，汽车出租公司的决策者开始时由于对市场不了解，开始汽车投放比例v1,v2,…,vl总有一定的盲目性，但经过顾客长时间在个网点租车与还车调整，选择更适合自己的租车与还车的网点，从上可知，各网点的汽车比例不是由汽车出租公司的决策者决定，而是由顾客，也即市场决定的，即服务人员的人数由市场调节决定.

[1] Cogburn R. The Ergodic Theory of Markov Chains in Random Eanvidom Environments [J].Z Wahrsch Verw Gebiete，1984,66:129-128.

[2] Cogburn R. On Direct Convergence and Peoriodicity for Transition Probabilities of Markov Chains in Random Environments[J].Ann Prob，1990,18(2):642-654.

[3] Orey S. Markov Chains with Stochastically stationary Transition Probability[J].Ann Prob，1991,19(3):907-928.

[4] Hu Di-he. The Relations Among Various Markov Chains[J].Wuhan Univ(Nat Sci Ed),2001,6(3):643-648.

[5] 肖争艳.随机环境中马氏链的极限性质 [D].武汉：武汉大学,2003.

[6] 郭光耀.随机环境马氏链的φ一不可约性[J].武汉化工学院学报,2006，28(4)：80-82.

[7] 李应求.双无限环境中马氏链的常返性及不变测度[J].中国科学,2001，31：695-701.

[8] 费时龙，任敏.随机环境中马氏链状态的常返性与暂留性[J].高校应用数学报A辑,2011，26(2)：187-194.

[9] 李应求.双无限随机环境中的常返马氏链 [J].数学学报,2007(5):141-152.

[10] 李应求.双无限随机环境中马氏链的暂留性[J].数学物理学报,2007,27(2):269-276.

[11] 宋明珠,姚毓才.随机环境马氏链的常返性与暂留性[J].重庆工商大学学报,2009,26(3):209-212.

[12] 宁小青.有限状态下随机环境马氏链的性质[J].三峡大学学报:自然科学版,2011(8)：695-701.