自重初应力对格构柱高墩-连续板梁桥动力特性的影响*
2012-01-04胡迎新鲁四平
胡迎新,鲁四平
(1.湖南中大设计院有限公司,湖南长沙410075;2.中南大学土木工程学院,湖南 长沙410075)
对于承受动力荷载的结构,固有频率和振型是结构设计的重要参数。如何通过现有的模态分析技术获得结构的准确动力特性是一个重要的问题。对于恒载较大的桥梁,自重初应力对动力特性的影响是不可忽略的。已有研究表明,对于悬索桥的模态分析,不经过恒载静力分析而直接进行模态分析可能得到错误的结果[1]。刘忠平等[2]研究了长沙湘江三汊矶大桥的动力特性及其影响因素,同样指出恒载形成的初应力会改变桥梁的固有频率,同时使振型改变和重组。对于其他类型的桥梁,目前尚缺乏相关研究去揭示自重初应力对动力特性的影响规律。宁波火车南站枢纽改造工程临时铁路桥(宁波桥)采用角钢格构柱作为桥墩,最大墩高达到22 m。作为采用有砟轨道的铁路桥梁,二期恒载很大,格构柱墩在桥梁自重作用下的初应力必然会影响到整桥的动力特性。本文基于ANSYS建立了包含轨道结构、梁板结构、格构柱墩、剪刀撑及桩-土作用的宁波桥精细有限元模型,在考虑和不考虑自重初应力2种情况下,通过子空间法求解包含局部振动和整体振动的全局模态,通过缩聚模态法求得宁波桥的整体振动模态。对2种情况下的全局模态和整体振动模态的分析结果进行比较研究,揭示自重初应力对格构柱高墩-连续板梁桥动力特性的影响规律,对模态分析的方法提出了新的认识。
1 有限元模型
宁波火车南站枢纽改造工程临时铁路桥全长132 m,桥面宽12.9 m,采用双线有砟轨道,设计列车时速120 km/h。上部结构采用24孔不等跨的现浇钢筋混凝土连续板梁桥,桥墩采用四肢缀板式角钢格构柱,基础采用柱下独立摩擦型桩基础。桥梁的动力特性受到桥各部分结构的质量、刚度、阻尼和边界条件的影响,在有限元模型中,除了准确考虑桥梁主体结构外,还应考虑轨道结构和桩-土作用。在有限元模型中,对轨道结构采用简化处理,仅建立钢轨、轨枕和道砟的模型,梁板结构则按实际截面和布置方式建立,模型中没有对格构柱截面进行简化,定义了相应的格构柱及支撑杆件截面。缀板式格构柱包含2种截面,无缀板处为四肢独立的角钢,有缀板处则形成封闭的箱型截面,支撑杆件均为槽钢。摩擦型桩由桩端和桩侧土共同提供竖向承载力,由桩侧土提供横向承载力。桩周土采用纵向、横向和竖向3个方向的“等代土弹簧”来模拟,等代土弹簧的刚度由土介质的m计算[3]。本文所建立的宁波桥有限元模型中,所选取的单元类型、单元数量及对应部件名称统计见表1。格构柱墩及剪刀撑体系局部有限元模型如图1所示,格构柱墩的2种截面及局部有限元模型如图2所示,桩-土作用等代土弹簧有限元模型如图3所示,宁波桥的整体有限元模型如图4所示。

表1 有限元模型单元数目统计表Table 1 Quantity statistics of elements in the FE model

图1 格构柱墩及剪刀撑有限元模型Fig.1 FE model of latticed column and brace

图2 格构柱墩有限元模型Fig.2 FE model of latticed column
图3 桩-土弹簧有限元模型Fig.3 FE model of pile-soil spring

图4 宁波桥有限元模型Fig.4 FE model of Ningbo Bridge
2 材料参数
根据现有工程技术资料及现场情况,本文所采用的计算参数见表2。
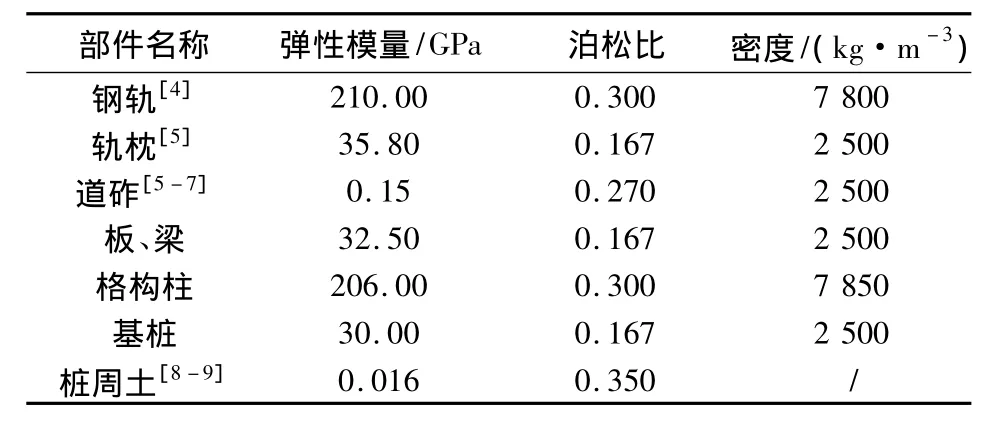
表2 材料参数表Table 2 Material properties in the FE model
3 研究结果与讨论
本文模态分析采用子空间法(Subspace iteration method)和缩聚模态法(Reduced method)。子空间法使用子空间迭代技术,它内部采用广义Jacobi迭代算法。该方法采用完整的刚度矩阵[K]和质量矩阵[M],计算精度很高。缩聚模态法采用HBI(Householder-Bisection-Inverse iteration)算法,在使用时必须指定主自由度(Master degrees of freedom),计算过程中将形成精确的[K]矩阵和近似的[M]矩阵,计算结果的精度取决于质量矩阵[M]的近似程度,质量矩阵[M]的近似程度又取决于主自由度的位置和数目。因此,主自由度的选取是缩聚模态法的关键。
当只对某些特定部位或特定方向的振动模态感兴趣时,选用缩聚模态法是很有效的。缩聚模态法就像是为模态分析添加了1个过滤器,把不感兴趣的振动模态全部都过滤,从而做到有的放矢,事半功倍。通过子空间法分析发现,宁波桥格构柱墩局部振动的模态较多。为了获得整体振动模态,必须采用缩聚模态法,选取桥面板的各个振动方向作为主自由度,把格构柱墩的局部模态全部“过滤”,因而,本文采用缩聚模态法求得的各阶模态,均是整体振动模态。
在考虑自重初应力和不考虑自重初应力2种情况下,分别采用子空间法和缩聚模态法求得宁波桥的前25阶模态。模态分析结果见表3,固有频率曲线如图5和图6所示,2种情况下的固有频率相对差值曲线如图7和图8所示。

图5 前25阶频率曲线(子空间法)Fig.5 Natural frequencies of the first 25 ranks(Subspace iteration)

图6 前25阶频率曲线(缩聚模态法)Fig.6 Natural frequencies of the first 25 ranks(Reduced)
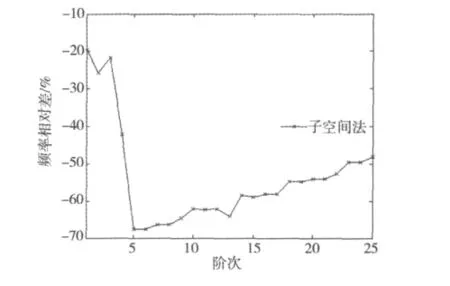
图7 前25阶频率相对差(子空间法)Fig.7 Relative difference of natural frequencies(Subspace iteration)

图8 前25阶频率相对差(缩聚模态法)Fig.8 Relative difference of natural frequencies(Reduced)
从表3可以看出:不考虑自重初应力时,桥面板水平向振动的模态先于竖向振动模态出现,说明水平向的刚度比竖向刚度低。考虑自重初应力时,格构柱墩的局部振动模态先于整体振动模态出现,说明格构柱墩在自重初应力作用下,由于几何刚度的影响,其组合刚度[10]明显降低。
从图5和图7可以看出:采用子空间法求得的模态,在考虑与不考虑自重初应力2种情况下,各阶频率的差异很大,且出现了较多的重频,重频所对应的振型往往是处于对称位置的格构柱墩的局部振动。由于2种情况下的振型不是一一对应的,所以,频率不能一一对应直接比较,而应比较相同振型所对应的频率才有意义。比较可知考虑自重初应力的第3,4,9和22阶振型分别与不考虑自重初应力时的第1,2,3和4阶振型相同,均表现为桥面板板的横向、纵向振动,它们的频率也是几乎相同的。对于振动位置相同的局部振动模态,考虑自重初应力时明显比不考虑自重初应力时的低。说明自重初应力对整体模态的频率影响较小,而对局部振动模态的频率影响很大。在桥面系及轨道结构的自重作用下,格构柱墩承受较大的压力,使得格构柱墩的局部振动模态提前出现,同时减小了前25阶频率的分布范围。
从图6和图8可以看出:采用缩聚模态法求得的模态,其前25阶频率的范围明显增大。在考虑与不考虑自重初应力2种情况下,频率几乎是一一对应相等的,且没有出现重频。采用缩聚模态法和子空间法求得的相同振型的频率是一致的,这说明本文主自由度的选取保证了模态分析的精度。前5阶频率的梯度比较明显,之后的频率梯度则较小,由于模态阶数的高低实际上反映了按相应振型振动的难易程度,可见各种竖向振动振型出现的难易程度相差不大,宁波桥的竖向振动必然是复杂多样的。考虑自重初应力时,前5阶固有频率的相对差值比其他各阶的大,说明自重初应力对低阶模态的影响较大,对高阶模态的影响较小。

表3 前25阶模态分析结果Table 3 Modal analysis results summary of the first 25 ranks
4 结论
(1)比较考虑和不考虑自重初应力2种情况下的子空间法分析结果,可知自重初应力对模态分析结果的影响主要体现在使各个振型出现的先后顺序重新调整,使格构柱墩的局部模态提前出现,且使格构柱墩的自振频率大幅度降低。对于振型相同的整体振动模态,自重初应力考虑与否几乎没有区别。
(2)考虑和不考虑自重初应力2种情况下,局部振动振型不存在对应关系,2种情况下的局部振动振型体现出较大差异,考虑自重初应力后,出现了较多桥面板与格构柱墩共同振动的振型。
(3)自重初应力对整体振动模态的影响很小,且对低阶模态的影响略大,对高阶模态的影响略小,2种情况下的固有频率几乎一一对应相等,振型一一对应相同。
(4)自重初应力仅对结构中轴向受力构件的局部振动模态有较大影响,不经过恒载静力分析而直接进行的模态分析,所得到的整体振动模态结果仍然是正确的,但局部振动模态结果不再适用。
[1]张 卉,王志清.悬索桥有限元建模及动力特性分析[J].华中科技大学学报:城市科学版,2006,23(2):25-27.ZHANG Hui,WANG Zhi-qing.FE modeling and dynamic response analysis of a suspension bridge[J].J of HUST:Urban Science Edition,2006,23(2):25 -27.
[2]刘忠平,戴公连.自锚式悬索桥有限元建模及动力特性影响因素研究[J].中外公路,2007,27(4):138 -142.LIU Zhong-ping,DAI Gong-lian.Finite element modeling and study on the influencing factors dynamic Characteristics of self- anchored suspension bridge[J].Journal of china& foreign highway,2007,27(4):138-142.
[3]TB 10002.5—2005,铁路桥涵地基和基础设计规范[S].TB 10002.5—2005,Code for design on subsoil and foundation of railway bridge and culvert[S].
[4]赵国堂.铁路轨道刚度的确定方法[J].中国铁道科学,2005,26(1):1 -6.ZHAO Guo- tang.Method for determining the rigidity of railway track[J].China Railway Science,2005,26(1):1-6.
[5]郝 赢.铁道工程[M].北京:中国铁道出版社,2002:30-32.HAO Ying.Railway engineering[M].Beijing:China Railway Press,2002:30 -32.
[6]翟婉明.车辆-轨道耦合动力学[M].北京:中国铁道出版社,2002.ZHAI Wan-ming.Vehicle-track coupling dynamics[M].Beijing:China Railway Press,2002.
[7]雷晓燕,陈水生.高速铁路轨道结构空间动力分析[J].铁道学报,2000,22(5):76 -80.LEI Xiao-yan,CHEN Shui-sheng.Space dynamic analyses for track structure of high speed railway[J].Journal of the China Railway Society,2000,22(5):76 -80.
[8]铁道部第一勘测设计院.铁路工程地质手册[M].北京:中国铁道出版社,1999.China Railway First Survey and Design Institute Group Ltd.Geological handbook of railway engineering[M].Beijing:China Railway Press,1999.
[9]周全能,那同伶.肖甬铁路宁波段淤泥质软土的工程地质特性探讨[J].路基工程,1997(2):30-33.ZHOU Quan-neng,NA Tong-lin.Investigate on the engineering characteristics of the soft soil in Xiao-Yong Railway ningbo section[J].Subgrade Engineering ,1997(2):30-33.
[10]R.克拉夫,J.彭津.结构动力学[M].北京:高等教育出版社,2006.Clough R,Penzien J.Dynamics of structures[M].Beijing:Higher Education Press,2006.
