框支剪力墙土-结构共同作用的抗震性能分析*
2012-01-04陆铁坚单晓菲
陆铁坚,单晓菲,蔡 勇
(中南大学土木工程学院,湖南长沙410075)
自20世纪80年代以来,高层建筑朝着复杂化、多功能化方向发展。为了满足建筑功能多样化的需求,框支剪力墙结构得到广泛应用[1]。目前对这种结构的研究也越来越多,但大部分设计都假设结构基础直接坐落在刚性的地基上,不考虑土-结构共同作用[2-3]。实际建筑物都是由上部结构、基础与地基土构成的整体,各部分相互影响、共同作用。这种假定将造成计算结果与实际工程不相符,而给建筑结构设计带来经济以及安全方面的问题[4-6]。框支剪力墙结构中的转换层会导致结构侧向刚度沿高度分布不均匀,从而显著影响地震作用下结构的动力响应[7],因而对框支剪力墙结构进一步开展基于土-结构共同作用的弹塑性抗震性能的分析研究十分必要。本文采用合理的计算假定,利用有限元软件ANSYS建立土-结构相互作用三维空间模型,对结构进行了弹塑性动力时程分析[8]。计算结果对类似的工程结构设计具有一定的参考价值。
1 计算模型和基本假定
1.1 模型参数

图1 结构平面布置图Fig.1 Structure floor plan
考虑土-结构共同作用下框支剪力墙结构的三维有限元分析是一个非常复杂的问题,如网格划分、接触单元的处理等都十分复杂。
若网格划分尺寸过大,则地震记录波动的高频部分很难通过,计算精度将大大降低。过细,则结构自由度太多,相应的计算时间和费用也会偏高。因此,合理地划分网格要满足经济和求解精度的平衡。另外,动力非线性分析网格划分应小到足以确定感兴趣的最高阶振型,捕捉到非线性效果。
根据研究表明,一般对于沿竖向传播的剪切波,其单元高度可取为其中:vs为剪切波速,fmax为截取的最大波动频率。平面尺寸主要取决于土层情况,一般来说可以取(3~5)hmax。本文将下部地基土体的划分成1 m3的小单元,上部剪力墙划成1 m2的面单元,非转换梁以1 m为单位划分,转换梁和框支柱为重要受力构件以0.5 m为单位细化。计算结果表明,这样对结构进行网格划分满足求解精度的要求。
对于土和结构接触面的处理,本文是直接利用ANSYS的接触单元来实现的,将接触界面处的土表面作为接触面形成接触单元(CONTAC170),基础底表面作为目标面形成目标单元(TARGET173),然后通过相同的实常数将对应的单元定义为1个接触对,并假定接触面上存在库仑摩擦。根据实际情况通过选择合理的参数采用接触类型Standard来模拟实现土-结构界面上的黏结、滑移、张开、再闭合的状态。ANSYS接触基本理论如下。
ANSYS里接触系统满足如下的平衡方程:

式中:左边表示内应力σ对虚应变δε做的虚功;右边第1项表示体力对虚位移δu做的虚功;第2项表示面力对虚位移δu做的虚功,右边最后一项为接触力对虚位移δu做的虚功。接触系统要满足平衡方程,同时还必须满足下面的接触条件。
综上所述,使用氨甲环酸可以显著减少脊柱转移肿瘤手术中的出血量。在氨甲环酸组中更少的患者术后需要输血及围手术期并未增加深静脉血栓形成的风险。
(1)法向条件:

式中:g为接触对之间的最短距离;λ为接触对之间牵引力的法向分量。
(2)切向条件:假设接触面是库仑摩擦因数为μ,令无量纲变量τ满足其中:t为接触对之间牵引力的切向分量;μλ表示接触对之间的库仑摩擦力。由库仑摩擦定理得到接触面上必须满足条件,而且当时时,

令ω为g和λ的函数,且方程ω(g,λ)=0的解满足法向条件;令ν为u和τ的函数,且方程ν(u,τ)=0的解满足切向条件。因此,接触条件可以表示为:

通过罚函数法或拉格朗日乘子法把以上条件引入到平衡方程中。将式(4)代入平衡方程(1),得到约束方程为
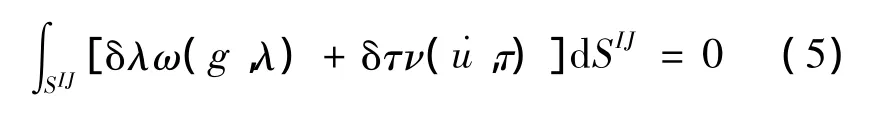
以上平衡方程以及接触条件都只考虑了静力接触状态。而本文考虑的是动力分析,在动力分析中分布体力还包括惯性力,而且在任何时刻,运动接触条件都必须满足接触体之间的位移、速度和加速度的协调性[9]。

表1 土的属性Table 1 Attributions of soil

表2 构件截面尺寸Table 2 Member of the section size
1.2 计算假定
(1)上部结构材料为弹性材料,符合双线性等效硬化屈服准则,地基土为弹塑性材料,符合Drucker-Prager屈服准则。
(2)地基土体连续,且不计时间与温度的影响。地基由基岩与覆盖于其上厚度为H的单一土层构成。
(3)钢筋混凝土基础埋置在土层中,土体坐落在基岩上,且土体与基岩的接触面水平,基岩为刚性体其位移为0。
(4)地基各边界面采用位移边界,忽略远场地基的影响。地基水平计算范围采用远置边界条件,理论上计算范围要L>Tc/2,取基础特征尺寸的5~10 倍[10-11]。本文取水平方向向外延伸 70 m,深度延伸45 m。
(5)钢筋混凝土基础与地基土侧面和底面之间非线性接触采用ANSYS接触对处理。
(6)模型均为弹性楼板,且不考虑水平地震作用折减。
2 转换层设置高度对结构抗震性能的影响
保持结构总高度64.5 m不变,调整结构层数,建立4个三维有限元计算模型进行分析[12]。各模型转换层设置高度如表3所示。采用弹塑性时程分析法计算,仅考虑水平地震作用。

表3 不同转换层设置高度分析模型Table 3 Transfer storey in different settings corresponding to different models
2.1 结构自振周期分析
模型前3阶振型自振周期见表4。由表4可知:

表4 模型前3阶振型自振周期Table 4 Natural period of the first 3 vibration mode s
(1)转换层设置高度对结构自振周期影响较小。当转换层位于5层以下时,随着转换层设置高度的增加,结构的整体刚度增强,自振周期略有减小;当转换层位于5层以上时,则刚好相反。
(2)结构模型的第一扭转周期和第一侧振周期比均小于规范中规定的值0.85[12]。这说明考虑土-结构共同作用后结构体系在平面和竖向布置上满足抗扭能力的要求,计算模型具有良好的整体性能,适合用于计算研究。
2.2 顶层位移分析
结构在地震作用下的顶层位移是结构延性的重要体现。为了比较结构在不同地震作用下的反映,本文选用了3条典型地震波(天津波、Taft波和ELCentro波),同时输入X和Y方向地震波,通过计算分别得到结构顶层位移时程曲线如图2~4所示。
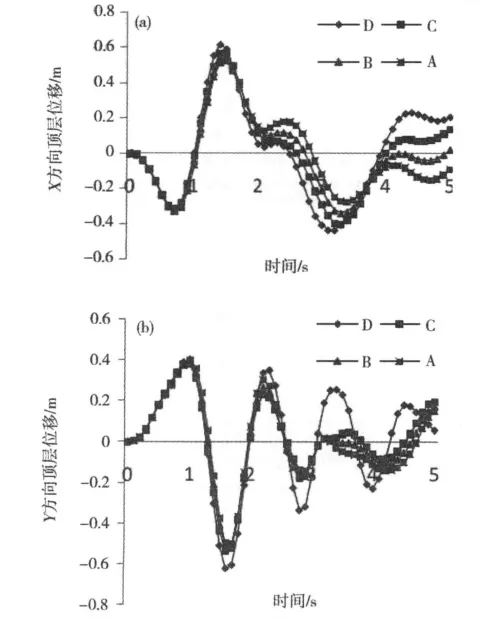
图2 天津波作用下顶层位移曲线Fig.2 Top storey displacement curves under Tianjin wave
在天津波作用下结构顶部控制点的横向位移最大,EL-Centro波次之,Taft波最小。说明同一水准条件下,结构对不同地震波反应相差较大,即输入地震波的频谱特性对结构的动力反应影响相当明显。因此,对结构进行弹塑性时程分析时,必须选择多条地震波进行计算。这与《建筑抗震设计规范》规定对结构进行弹塑性时程分析时至少选择2+1条地震波进行计算是一致的[2]。
从图2~4可以看出:结构在不同地震波作用下,顶层最大位移随转换层位置提高而减小,转换层超过5层后顶层位移呈增大趋势。结构顶层位移随时间历程呈发散趋势,在前段时间顶点位移曲线基本相似,到后面差异趋于明显,并且结构在顶部控制点最大位移出现的时间随着转换层位置的提高而稍提前。

图3 Taft波作用下Y方向顶层位移曲线Fig.3 Top storey displacement curves under Taft wave
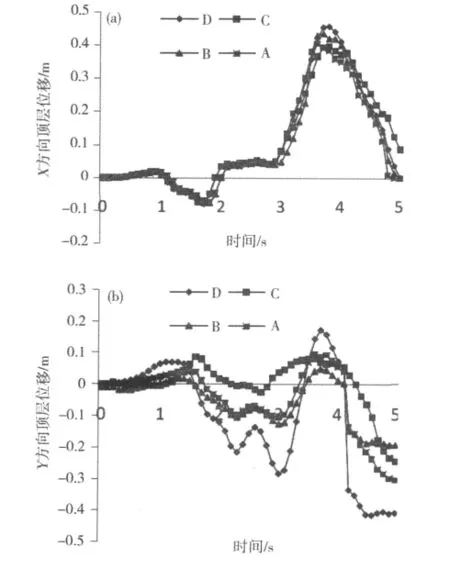
图4 EL-Centro波作用下顶层位移曲线Fig.4 Top storey displacement curves under EI-Centro wave
2.3 结构侧移及层间位移角
结构侧移和层间位移角是反映结构在地震作用下受力性能的重要指标。结构在天津波作用下地震反应最大,因此,下面均以天津波作用下计算数据为例进行分析。

图5 楼层位移曲线Fig.5 Storey displacement curves
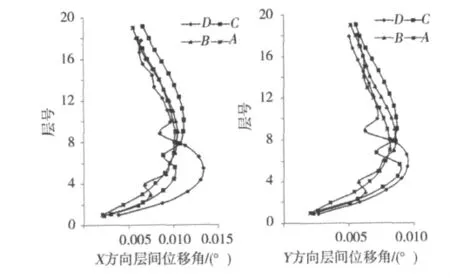
图6 层间位移角曲线Fig.6 Inter- storey drift angle curves
由图5和图6可以看出:结构最大Y方向侧移较X方向略有减小,层间位移角在转换层附近发生明显突变,使得结构层间位移较大值都集中在结构的中上部楼层,随着转换层位置的提高突变越来越剧烈。因此,在进行高层框支剪力墙结构设计时,应该对中上部楼层加强并采取相应的减小层间位移的措施。
2.4 结构等效侧向刚度比
由表5可看出:转换层在5层以下时,其等效侧向刚度比随转换层位置的提高逐渐增大;当转换层位于7层时,等效侧向刚度比不满足规范要求(根据《高层建筑混凝土结构技术规程》E.0.2底部大空间层数大于1层时其转换层上部与下部等效侧向刚度比抗震设计时不应大于1.3。当转换层设置在3层及3层以上时,其楼层侧向刚度尚不应小于相邻上部楼层侧向刚度的60%[13])。可以判断框支剪力墙结构转换层高度可以适当提高,但是,为了避免转换层附近刚度突变过大,转换层上下的等效侧向刚度比宜控制在0.8~1.3之间,且应在转换层附近采取相应的措施增强连接处的延性。
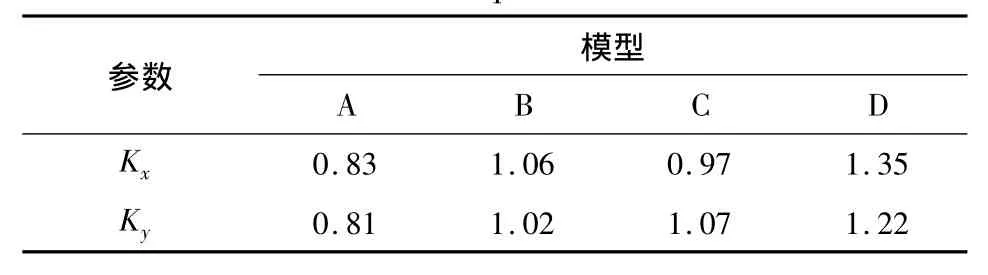
表5 结构的等效侧向刚度比Table 5 The ratios of equivalent lateral stiffness
2.5 结构剪力分析
由于钢筋混凝土材料的特性,剪力是在地震作用下对建筑物造成破坏的重要因素。表6所示为框支柱所承担的剪力。

表6 框支柱所承担的剪力Table 6 Shearing force of column kN
由于楼板变形,框支柱所分担的总剪力不可能均匀分配给各框支柱,承受剪力最大值的框支柱发生在框支部分最顶层的中柱(平面图中的3和4号柱),而且框支柱剪力值随转换层位置的提高而增大[14]。一方面是因为结构本身的自重增加导致剪力增大,另一方面是因为转换层位置影响地震剪力的分配。
根据表6中数据可以得出:随着转换层位置的提高,转换层的框支柱所承担的剪力占楼层总地震剪力的比值逐渐增加(从转换层在1层时的35.8%提高到在7层时的90.8%)。因此,转换层框支柱要重点加强。
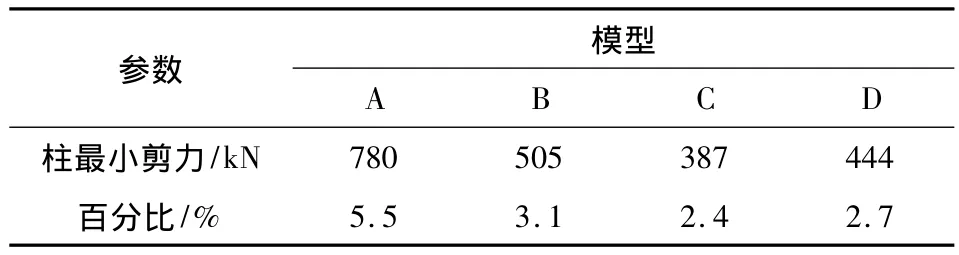
表7 框支柱最小剪力百分比Table 7 the percentage of the least shearing force of column
高规第10.2.7条的规定:当每层框支柱数目不多于10根,框支层为1~2层时,每根柱所受的剪力应至少取基底剪力的2%;当框支层为3层及3层以上时,每根柱所受的剪力应至少取基底剪力的3%。表7中的数据显示出转换层位置位于5层及以上时,结构框支柱的最小剪力小于规范要求的最小值。因此,设计时要注意当转换层位置超过3层时,框支柱的最小设计剪力至少要取基底剪力的3%。
3 结论
(1)运用ANSYS建立框支剪力墙-土-结构共同作用空间模型对结构地震反应进行分析,能够更真实地反映结构的抗震性能。
(2)转换层的设置高度对结构自振周期的影响较小。当转换层位于5层以下时,自振周期随转换层位置的提高略有减小;当转换层位于5层以上时,结构整体刚度削弱,自振周期反而呈增大趋势。
(3)顶层最大位移随转换层位置提高而减小,转换层超过5层后顶层位移呈增大趋势,且随时间历程呈发散趋势。输入地震波的频谱特性对结构的动力反应影响明显。所以,对结构进行弹塑性时程分析时,必须选择多条地震波进行计算。
(4)结构较大层间位移角集中在结构的中上部;框支柱剪力最大值发生在转换层中柱,随着转换层位置的提高,转换层框支柱所承担的剪力占楼层总地震剪力的比值逐渐增加。因此,设计框支剪力墙结构时,要对对框支柱格外加强,还应该对中上部楼层采取相应的减小层间位移的构造措施。为限制转换层附近刚度突变和结构变形,转换层上下的等效侧向刚度比宜控制在0.8~1.3。
[1]董海河,李振宝,马华.框支剪力墙耗能结构抗震性能研究 [J].世界地震工程,2008,24(3):101 -106.DONG Hai-he,LI Zhen-bao,MA Hua .Seismic performance study on energy dissipation structure of shear wall supported on a frame - shear wall structure[J].World Earthquake Engineering,2008,24(3):101 -106.
[2]GB 500ll—20l0,建筑抗震设计规范[S].GB 50011—20l0,Code for seismic design of building[S].
[3]刘洁平,张令心.高层建筑土-结构相互作用地震反应简化评估方法[J].土木工程学报,2010,43(12):28 -34.LIU Jie-ping,ZHANG Ling-xin.A simplified assessment method for seismic response analysis of soil- structure interaction of high - rise buildings[J].China Civil Engineering Journal,2010,43(12):28 -34.
[4]荣 峰,刘建伟,王 奎,等.基于土-结构相互作用的高层建筑三维地震反应分析[J].工程抗震与加固改造,2011,33(3):1 -6.RONG Feng,LIU Jian-wei,WANG Kui,et al.3D Seismic response of tall building based on soil- structure interaction[J].Earthquake Resistant Engineering and Retrofitting,2011,33(3):1 -6.
[5]何 涛,何三喜,孙伶俐.考虑土与上部结构共同作用的双塔楼连体结构地震反应分析[J].工程抗震与加固改造,2007,29(6):41 -45.HE Tao,HE San-xi,SUN Ling-li.Seismic response analysis of a double-tower connecting structure considering dynamic soil- structure interaction[J].Earthquake Resistant Engineering and Retrofitting,2007,29(6):41 -45.
[6]齐永正.地基-基础-上部结构共同作用三维数值模拟分析[J].岩土力学,2007,28(增刊):859-862.QI Yong-zheng.Three - dimension numerical simulation and analysis of interaction of foundation-subsoil and superstructure[J].Rock and Soil Mechanics,2007,28(Supp):859-862.
[7]韩小雷,何伟球,郑 宜,等.框支剪力墙结构楼层侧向刚度比初探[J].工程力学,2010,27(4):125 -132.HAN Xiao-lei,HE Wei-qiu ,ZHENG Yi,et al.Preliminary study of inter-story lateral stiffness ratio in framesupported shear- wall structure[J].Engineering Mechanics,2010,27(4):125 -132.
[8]陆铁坚,李丽梅,林国章.用ANSYS分析高层钢-混凝土混合结构的地震反应[J].铁道科学与工程学报,2007,4(3):32 -37.LU Tie-jian,LI Li-mei,LIN Guo-zhang.Application of ANSYS to seismic response analysis of tall steel-concrete hybrid structure[J].Journal of Railway Science and Engineering,2007,4(3):32 -37.
[9]吕西林.复杂高层建筑结构抗震理论与应用[M].北京:科学出版社,2007.LV Xi-lin.Theory and application of seismic for complex high -rise structures[M].Beijing:Science Press,2007.
[10]刘晶波,吕彦东.结构-地基动力相互作用问题分析的一种直接方法[J].土木工程学报,1998,31(3):55-64.LIU Jing-bo,LÜ Yan-dong.A direct method for analysis of dynamic soil- structure interaction[J].China Civil Engineering Journal,1998,31(3):55 -64.
[11]刘立平.水平地震作用下桩-土-上部结构弹塑性动力相互作用分析[D].重庆:重庆大学,2004.LIU Li-ping.Study on pile - soil- superstructure elasto-plastic dynamic interaction under the horizontal earthquake action[D].Chongqing:Chongqing University,2004.
[12]舒兴平,毛健宇,黄 伟,等.型钢混凝土框支框架-混凝土核心筒结构抗震性能分析[J].湖南大学学报,2010,37(12):7 -12.SHU Xing-ping,MAO Jian-yu,HUANG Wei,et al.Anti-seismic performance analysis of steel reinforced concrete frame supported by frame concrete core structure[J].Journal of Hunan University,2010,37(12):7 -12.
[13]JGJ 3—2002,高层建筑混凝土结构技术规程[S].JGJ 3—2002,Technical specification for concrete structure of tall building[S].
[14]张风岭,周德源.影响框支剪力墙结构抗震性能的主要因素[J].住宅科技,1998(10):17-20.ZHANG Feng-ling,ZHOU De-yuan.Study on influence factor of superstructure and subsoil interaction effect[J].Residence Technology,1998(10):17 -20.
