均衡完全三部图 K3（n）的线性3－荫度

王苒群，左连翠

（天津师范大学 数学科学学院，天津 300387）

均衡完全三部图K3（n）的线性3－荫度

王苒群，左连翠

（天津师范大学 数学科学学院，天津 300387）

考虑均衡完全三部图K3（n）的线性3－荫度.利用路分解的方法给出了K3（n）的线性3－荫度la3（Κ3（n））当n≡1，2，3（mod 4）时的比较紧的上界，利用线性k－荫度的基本理论分别得到了它们的下界，进而得到了特殊情况下均衡完全三部图K3（n）的线性3－荫度的确切值.

线性k－森林；线性k－荫度；均衡完全三部图

本研究所涉及的图都是简单图，即它们是有限的、无向的、无自环并且没有重边的图.图的一个独立集是顶点集的一个子集合，其中的顶点是两两不相邻的［1］.称图G是一个m－部图，如果它的顶点集合V（G）可以划分为m个独立集，而这些独立集称为m－部图G的分裂集.一个完全m－部图G首先是一个m－部图，并且边uv∈Ε（G）的充要条件是u和v属于不同的分裂集.当m≥2时，将完全m－部图记为Κn1，n2，…，nm，其中n1，n2，…，nm分别是它的分裂集的基数.若n1＝n2＝…＝nm＝n，则称此完全m－部图为均衡完全m－部图，记为Κm（n）.当m＝3时，这样的图就称为均衡完全3－部图，记作Κn，n，n或Κ3（n）.

图G的一个分解就是将这个图分成一系列的子图，使得图G的每条边恰出现在其中的一个子图中.如果图G有一个分解G1，G2，…，Gd，就称G1，G2，…，Gd分解了图G，或称G能分解为G1，G2，…，Gd.

线性k－森林是每一个连通分支均为长度不超过k的路的图.一个图G的线性k－荫度是将图G的边集合分解成的线性k－森林的最少数目，用lak（G）表示.

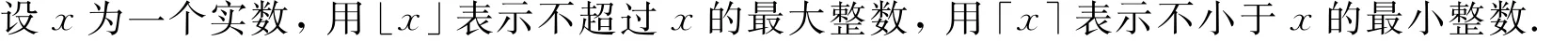
图的线性k－荫度的概念首先由Habib等［2］提出.它是边着色的一种很自然的推广.很显然，一个线性1－森林是由一个匹配导出的，并且图G的线性1－荫度等于它的边色数（或称色指数），即la1（G）＝χ′（G）.而且，一个图G的线性k－荫度lak（G）也是一般线性荫度la（G）（或者la∞（G））的一个加细，一般的线性荫度是图G的边集合能分解成的线性森林（每个连通分支都是路的图）的最少数目，此时每个分支都是没有长度限制的路.1982年，Habib等提出了下述猜想，估计出了lak（G）的一个上界.

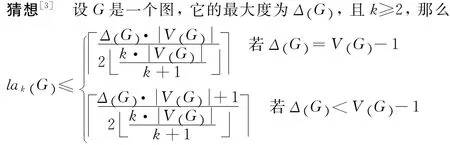
目前为止，已有的相关结果都是支持此猜想的，尤其是对于结构特殊的图，如树［2，4，5］、立方图［6－8］、正则图［9－10］、可平面图［11］、均衡完全2－部图［12－13］和完全图［6，12，14，15］等，此猜想都是成立的，但对于一般图，此猜想尚未得到证明.

1 预备引理

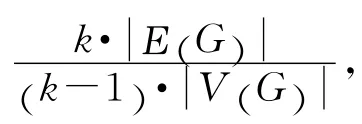
2 主要结论

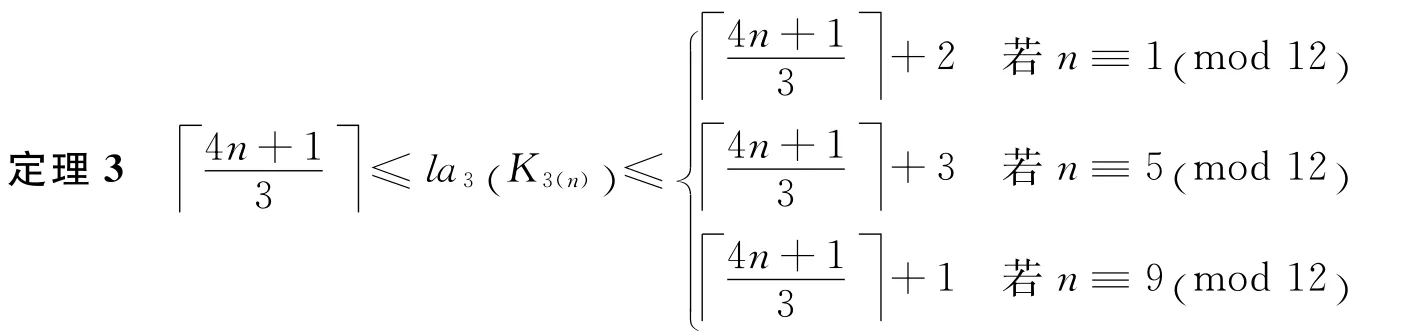
［1］ BONDY J A.Graph Theory with Applications［M］.New York：MacMillan Press，1976.

［2］ HABIB M，PEROCHE B.Lak－arboricitélinéaire des arbres［J］.Discrete Math，1983，17：307－317.

［3］ HABIB M，PEROCHE B.Some problems about linear arboricity［J］.Discrete Math，1982，41：219－220.

［4］ CHANG G J.Algorithmic aspects of lineark－arboricity［J］.Taiwanese J Math，1999，3：73－81.

［5］ CHANG G J，CHEN B L，FU H L，et al.Lineark－arboricities on trees［J］.Discrete Appl Math，2000，103：281－287.

［6］ BERMOND J C，FIUQUET J L，HABIB M，et al.On lineark－arboricity［J］.Discrete Math，1984，52：123－132.

［7］ JACKSON B，WORMALD N C.On the lineark－arboricity of cubic graphs［J］.Discrete Math，1996，162：293－297.

［8］ THOMASSEN C.Two－coloring the edges of a cubic graph such that each monochromatic component is a path of length at most 5［J］.Journal of Combinatorial Theory，1999，75：100－109.

［9］ ALDRED R E L，WORMALD N C.More on the lieark－arboricity of regular graphs［J］.Austral J Combin，1998，18：97－104.

［10］ALON N，TEAGUE V J，WORMALD N C.Linear arboricity and lineark－arboricity of regular graphs［J］.Graphs Combin，2001，17：11－16.

［11］LIH K W，TONG L D，WANG W F.The linear 2－arboricity of planar graphs［J］.Graphs Combin，2003，19：241－248.

［12］CHEN B L，HUANG K C.On the lineark－arboricity ofKnandKn，n［J］.Discrete Math，2002，254：51－61.

［13］FU H L，HUANG K C.The linear 2－arboricity of complete bipartite graphs［J］.Ars Combin，1994，38：309－318.

［14］CHEN B L，FU H L，HUANG K C.Decomposing graphs into forests of paths with size less than three［J］.Austral J Combin，1991，3：55－73.

［15］YEN C H，FU H L.Linear 2－arboricity of the complete graph［J］.Taiwanese J Math，2010，14：273－286.

［16］FU H L，HUANG K C，YEN C H.The linear 3－arboricity ofKnandKn，n［J］.Discrete Math，2008，308：3816－3823.

［17］YEN C H，FU H L.Linear 3－arboricity of the balanced complete multipartite graph［J］.Appl Math，2007，50：33－46.

Linear 3－arboricity of balanced complete tripartite graphΚ3（n）

WANGRan－qun，ZUOLian－cui
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

The linear 3－arboricity of balanced complete tripartite graphK3（n）is studied.It is obtained that the sharp upper bounds of linear 3－arboricityla3（K3（n））whenn≡1，2，3（mod 4）by using the method of path－factorization，as well as the lower bounds by using the elementary theory of lineark－arboricity.And then the exact values of linear 3－arboricity of balanced complete tripartite graphK3（n）in some special cases are determined.

lineark－forest；lineark－arboricity；balanced complete tripartite graph

O157.5

A

1671－1114（2012）02－0010－08

2011－10－09

天津师范大学引进人才基金资助项目（5RL066）

王苒群（1987－），女，硕士研究生.

左连翠（1964－），女，教授，主要从事图论及其应用方面的研究.

（责任编校 马新光）