音频大地电磁磁场传感器的研制

陈兴朋，宋 刚，周 胜，席振铢，王 鹤

(1. 中南大学 有色金属成矿预测教育部重点实验室，长沙 410083；2. 中南大学 地球科学与信息物理学院，长沙410083；3. 长沙五维地科勘察技术有限责任公司，长沙 410205)

利用远处雷电活动作为场源的音频大地电磁法(AMT)，具有成本低，效率高，勘探深度大(通常可达2km)，不受高阻层屏蔽和对低阻体具有较高的分辨能力等优点，近年来在地热、油气藏和煤田探测及固体矿产深部找矿等领域得到了广泛的应用，并有着非常广阔的应用前景[1]。但是，由于天然电磁场的信号十分微弱，特别是音频范围内磁分量的信号十分微弱。图 1所示为一幅全球磁场强度平均振幅谱特征图[2]，该图是1967年Compbell的研究成果。从图1可以看出，音频大地电磁场磁信号幅值为毫伽玛数量级。因此，音频大地电磁仪要求磁场传感器具有高灵敏度、高磁场分辨率和宽频带等性能，以便检测微弱的磁场信号[3]，而感应式磁场传感器无论是在灵敏度、磁场分辨率、带宽方面，还是在便携性方面都能够胜任[4]。

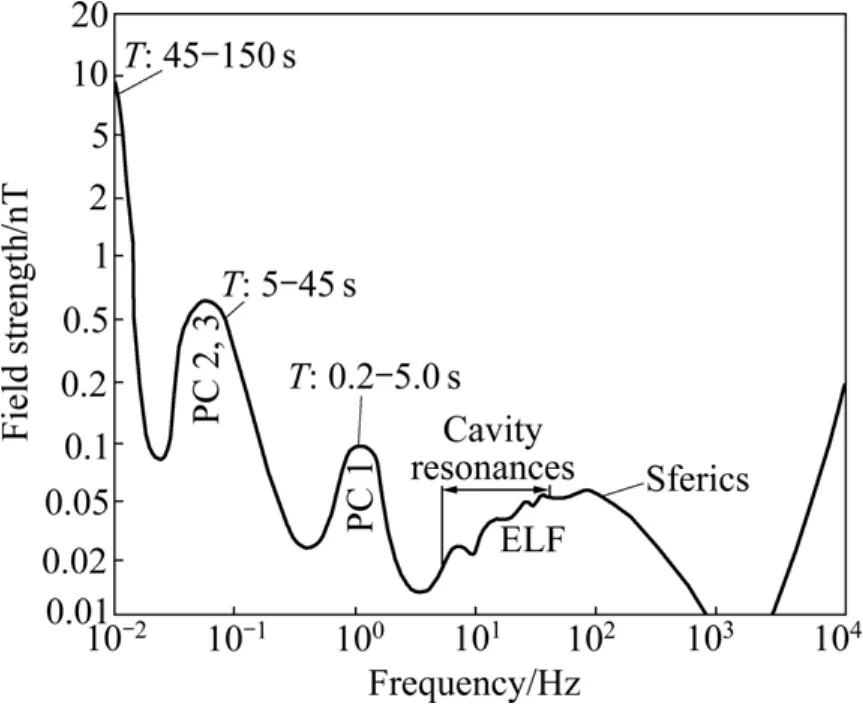
图1 大地磁场强度平均振幅特征谱[2]Fig. 1 Typical average amplitude spectrum of geomagnetic variations[2]

目前，市场上用于音频大地电磁测深的磁场传感器大部分都来自欧美，性能优异，频带宽，噪声低，灵敏度高，如德国METRONIX公司生产的MFS-07、美国ZONGE公司生产的ANT-5/6和EMI公司生产的BF-6/10、加拿大PHEONIX公司生产的AMTC-30、乌克兰生产的LEMI-118/120等。而国内音频大地电磁磁场传感器主要依赖进口，但价格昂贵，且对于高灵敏度的磁场传感器，国外对我国出口限制，严重制约着我国电磁法物探装备的发展[5]。为适应地质勘探工作需要和加速仪器的国产化，本文作者对音频大地电磁磁场传感器进行研究，设计了一种灵敏度曲线在1 Hz～9.8 kHz频段范围内不随频率变化的磁场传感器，以解决天然电磁场音频范围内磁信号十分微弱和动态范围大的问题，提高检测精度。

1 感应式磁场传感器的基本原理

感应式磁场传感器的原理是基于法拉第电磁感应定律[6]，如果线圈的匝数为 N，穿过磁芯的磁通量为Ф，磁芯的有效磁导率为 μc，磁芯的有效横截面积为S，平行于磁芯的外部磁感应强度为B，那么线圈的感应电压为

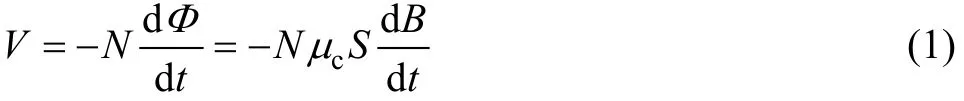
在频率域中，线圈的感应电压为

式中：ω为角频率。线圈的灵敏度系数(SF)为

在理想的情况下，根据式(2)，线圈的感应电压是随着频率的增加而呈线性增加的，但是由于感应线圈存在着直流电阻 R，电感 L，还有寄生电容 C，形成了谐振电路，使得感应电压V变得更加复杂。图2所示为线圈感应电压的典型频率特性图。从图2可以看出，式(2)只在谐振频率以下的频段范围内成立。

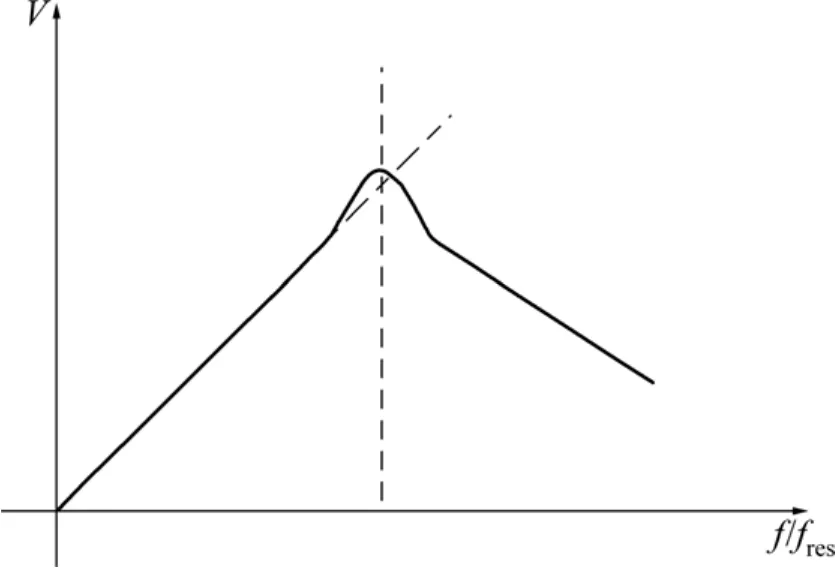
图2 线圈感应电压频率特性图(虚线为理想感应电压，实线为实际感应电压)Fig. 2 Typical frequency characteristic of an induction coil(Solid line—amplitude-frequency response of an induction coil output peak voltage V in resonance mode (fres is resonance frequency); dashed line—ideal shape of this response)

2 磁芯和线圈结构的设计分析

通过分析式(3)可知，感应线圈的灵敏度正比于线圈的匝数N，磁芯的有效横截面积S和有效磁导率μc。为了获得最佳的磁场接收效果，就必须使感应线圈在所要求的频带内具有最大的灵敏度。因此尽可能使得这三项的乘积最大[7]。

2.1 磁芯有效磁导率的设计分析

首先分析磁芯的有效磁导率μc。为了获得尽可能大的有效磁导率值，采用初始磁导率μr比较高的软磁材料，如坡莫合金、无定形材料。但是由于退磁系数的存在，使磁芯的有效磁导率远小于软磁材料的初始磁导率。磁芯的有效磁导率由下式给出[8]：

式中：Nd为退磁系数。对于长径比为m的旋转椭圆体磁芯，其退磁系数并不依赖于软磁材料的初始磁导率μr，而依赖于磁芯的形状结构，STONER给出了准确的计算公式[9]：

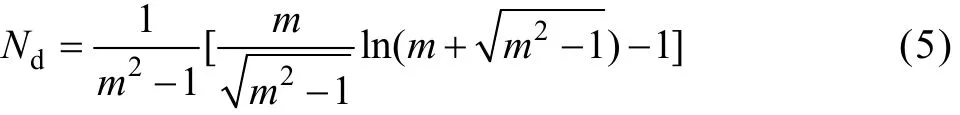
式中：m=l/d，l为磁芯的长度，d为磁芯的直径。对于细长椭圆体，式(5)可简化为

软磁材料的初始磁导率μr会随着时间和温度的改变而改变，为了提高磁场传感器的稳定性和环境适应性，就必须保证有效磁导率μc为常数。因此，对退磁系数Nd(磁芯的形状结构)和初始磁导率μr(软磁材料的选择)的设计分析尤为重要。图3[10]给出了在长径比m一定的情况下，保证细长圆柱体磁芯有效磁导率μc为常数时，软磁材料初始磁导率μr的最小值。例如，采用长径比m=50的细长圆柱体磁芯，那么就必须要求软磁材料的初始磁导率μr≥30 000，否则，随着时间和外部环境的变化，磁场传感器的灵敏度就会变得不稳定。

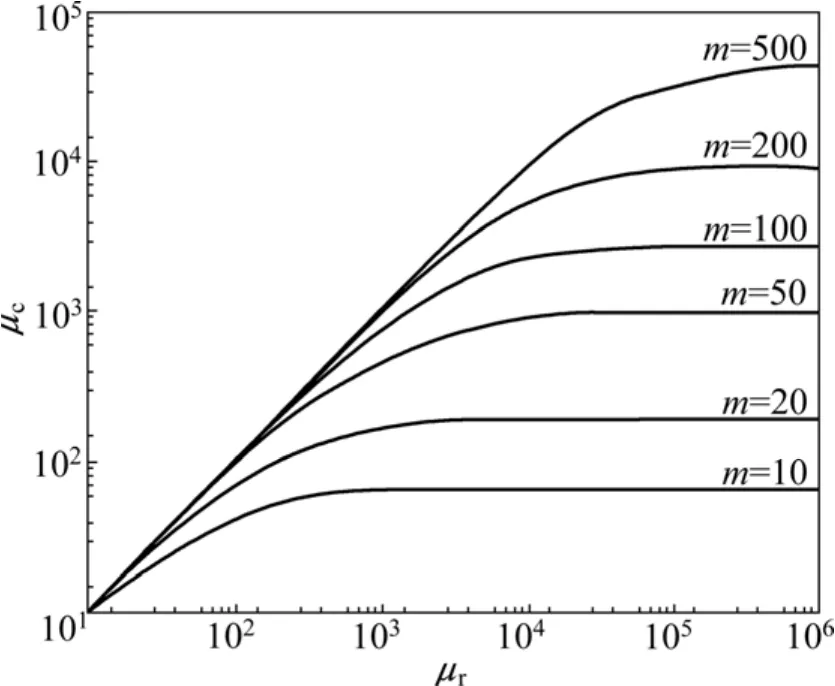
图3 长径比m不同时细长圆柱体磁芯有效磁导率μc随初始磁导率μr的变化曲线Fig. 3 Core permeability μc of cylindrical rods versus material permeability μr with different length-to-diameter ratios m of rod

磁芯的有效磁导率μc越大，磁场传感器的灵敏度也就越大，因此，通常采用细长形状的磁芯。在综合考虑磁场传感器的便携性和实用性的情况下，一般选择磁芯的长径比 50≤m≤100，软磁材料的初始磁导率μr≥50 000，这时磁芯的有效磁导率μc达到2 500，并且磁场传感器的灵敏度随软磁材料初始磁导率μr的变化很小。

2.2 磁芯有效横截面积的设计分析

从式(3)可知，磁芯的有效横截面积S也直接影响着磁场传感器的灵敏度。但是从上面对磁芯有效磁导率的分析可知，在设计磁芯有效磁导率时所设计要求的长径比m=l/d已经从另一方面决定了磁芯的有效横截面积。如果增大磁芯的有效横截面积 S，也就等于增大磁芯的直径 d，从而减小了磁芯的长径比 m，进而减小了磁芯的有效磁导率μc，这样就削弱了通过增大磁芯有效横截面积来提高磁场传感器灵敏度的作用。EUGENE和ASAF[11]通过在细长磁芯两端各附加上一块“磁通集中块”的方法克服了这个缺点，这样在增加磁芯有效横截面积的同时却不会改变磁芯的长径比m。当“磁通集中块”的直径Dc和磁芯的直径d之比约为5时，磁场传感器的灵敏度增加了2倍。

2.3 线圈匝数和绕组的设计分析

实际上，一味地增加线圈匝数来提高磁场传感器灵敏度的方法并不可取。因为铜导线存在直流电阻，增加线圈匝数的同时也增加了感应线圈的直流电阻和电阻产生的热噪声，这样就会使感应线圈的信噪比恶化。而如果在增加线圈匝数的同时采用线径大的铜导线，这样又会增加线圈的质量。理论和实验研究表明，磁场传感器的灵敏度阈值取决于线圈的质量，所以磁场传感器的灵敏度主要是由线圈的质量决定，而线圈匝数的选择主要是用于感应线圈和前置放大器的噪声匹配[12]。

事实上，线圈的绕组分布同样也会影响磁场传感器的灵敏度。铜导线不是直接绕在磁芯上，而是绕在传感器骨架上，这样线圈就有一个外径De和一个内径Di，满足 De＞Di＞d，并且如果它们之间的值相差越大，那么磁场传感器的灵敏度就越低。因此，磁场传感器的灵敏度和感应线圈的平均半径 Dm=(De+Di)/2成反比的关系。对于一个磁芯线圈系统，感应线圈的平均半径和磁芯的有效磁导率还满足μc≡Dm−3/2。

线圈绕组长度ln同样也会影响磁场传感器的灵敏度。事实上，磁芯中间的有效磁导率最大，灵敏度最高，两端最小。并且对于细长棱柱杆状磁芯，其中心的有效磁导率μcc由下式得出：

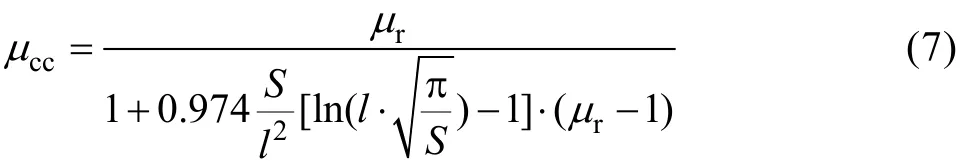
因此，为了避免边缘效应和获得较高的灵敏度电压，线圈绕组长度ln要比磁芯长度l小，但是线圈绕组长度也不能太短，否则，相同匝数的铜线长度将变长，导致线圈直流电阻变大，其他参数如寄生电容和交流电阻也将变坏。一般建议ln≈(0.5～0.7)l[13]。同时为了减小寄生电容，需要将线圈分段绕制，然后将每段线圈串联起来，电容串联时会成倍减小，这样可以减小总的寄生电容[14]。

在绕组长度为ln的情况下，磁芯有效磁导率的平均值 μcca为

3 磁场传感器的设计制作

音频大地电磁仪磁场传感器检测的是频率范围为0.1～8 192 Hz的微弱天然磁场信号，并且该天然磁场信号在2 kHz附近有一局部最小值且小于1 pT。为了检测到这么微弱的磁场信号，将磁场传感器的谐振频率设计在1～5 kHz之内，因为在谐振频率附近传感器的灵敏度最佳。由线圈的设计分析可知，磁场传感器的灵敏度阈值取决于线圈的质量。因此，在给定线圈质量的情况下，若选择线径小的铜线，虽然可以绕更多的匝数，但是感应线圈的电感和寄生电容会限制磁场传感器的频带；若选择线径大的铜线，虽然可以减小线圈的直流电阻，但是前置放大器的噪声水平会大于线圈电阻产生的热噪声。为了得到合适的谐振频率和考虑噪声匹配问题，选择铜线的线径为0.45 mm，线圈的匝数为12 000匝，同时将线圈分10段绕制。

由磁芯的设计分析可知，磁场传感器的灵敏度和磁芯的有效磁导率、有效横截面积成正比，但是在选定磁芯长度l时，有效磁导率和横截面积是相互制约的关系，因此，在兼顾有效磁导率和有效横截面积的同时，选择长度l=600 mm，横截面为19 mm×19 mm的磁芯。磁芯由初始磁导率μr=120 000，电阻率ρ=90 μΩ·cm3，厚度为Δ=35 μm的铁基纳米晶合金带材层叠而成。磁芯的等效直径为21.4 mm，由式(4)和式(5)得有效磁导率μc=259。

因为磁芯的有效磁导率并不是均匀分布的，在磁芯中点有效磁导率最大，在两端有效磁导率最小，因此，为了得到比较的高灵敏度和避免边缘效应，选择绕组的长度ln=360 mm。由式(7)和式(8)可得，在绕组长度ln=360 mm时磁芯有效磁导率的平均值为μcca=310。

对于 μc=259时，由式(3)计算得线圈的灵敏度系数SF=7.05 μV/(nT·Hz)。当考虑线圈的绕组宽度时，将计算得到的μcca=310代入式(3)计算得线圈的灵敏度系数SF=8.44 μV/(nT·Hz)。将磁场传感器置于一大螺旋线圈中心，然后给线圈供已知电流产生均匀磁场以此来测量线圈的灵敏度系数，实验测得 SF=7.94 μV/(nT·Hz)，与理论计算的结果非常吻合。

4 前置放大电路和磁场传感器的频率响应

没有经过电路调制的感应线圈，当频率超过谐振频率后，线圈的感应电压就会急剧下降，因此，能有效利用的频带只能是谐振频率的一侧，而且感应电压随频率呈线性变化，动态范围比较大。这样既限制了磁场传感器的频带范围，又不利于音频大地电磁仪对磁场信号的采集接收。为了扩展频带，充分利用谐振频率，本设计采用磁通负反馈的技术和低频电路补偿的方法来调制感应线圈产生的电压信号。这样既扩展了频带，又使得磁场传感器的频率响应曲线比较平坦。

磁通负反馈的原理是将线圈的感应电压放大后经反馈电阻转换成电流量，利用绕在感应线圈外侧的反馈线圈产生反馈磁场，进而对被测磁场形成负反馈，使磁场传感器形成闭合的磁通反馈回路[15]。磁通负反馈原理如图4所示。

图4中：Rsc、C、Lp分别是感应线圈的电阻、寄生电容和电感，Ls为反馈线圈的电感，Rfb为反馈电阻，V为线圈的感应电压；G为电路的放大倍数，G=1+R1/[R2(1+jωR1C1)]；M 为感应线圈和反馈线圈之间的互感，设k为互感系数，当两线圈紧密耦合时k=1，

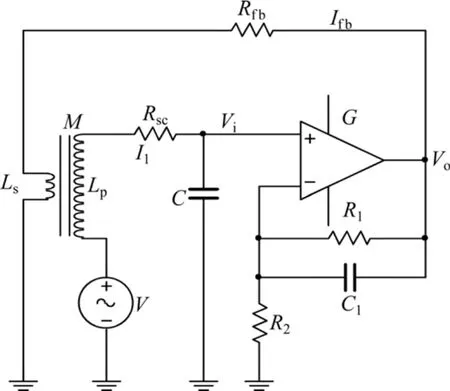
图4 磁通负反馈原理Fig. 4 Principle diagram of magnetic flux negative feedback

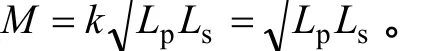
由图4可知，磁场传感器的线圈部分是一个振荡电路，整个反馈系统的传输函数如下：

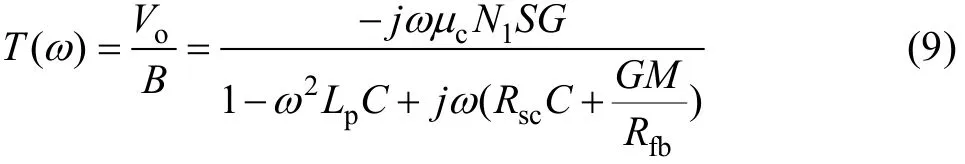
式中：N1是感应线圈的匝数。由文献[6]可知，其低频截止频率fL和高频截止频率fH分别如下：

并且在fL和fH之间，磁场传感器的灵敏度响应曲线为一平坦曲线，且幅值为

式中：μ0是真空中的磁导率，N2是反馈线圈的匝数，λ=1.85−1.1ln/l为校正系数。

当频率f＜fL时，磁场传感器的灵敏度响应曲线并不平坦，而是随频率呈线性变化。为了获得在全频段比较平坦的灵敏度曲线，对磁场传感器进行低频电路补偿。电路补偿的基本思想是在谐振频率两边按曲线的梯度进行放大，而在谐振频率点附近及其周围很小的区域保持其信号幅度不变[16]。

本设计采用螺旋线圈产生均匀磁场来测试感应线圈的频率响应。由于螺旋线圈只需很小的功率就能产生适合于磁场传感器标定用的磁场强度，并且体积小、产生的磁场分布比较均匀、使用灵活方便等优点，适合于磁场传感器的现场测试标定[7]。给螺旋线圈供带宽为100 kHz的白噪声，产生激励磁场，并将感应线圈置于螺旋线圈中心，通过数据采集卡采集激励信号和感应线圈的响应信号，将采集的数据通过 Labview虚拟仪器进行快速傅里叶变换，就可以得到感应线圈的频率响应曲线。图5所示为没有经过电路调制的感应线圈频率响应曲线。从图5可以看出，线圈的谐振频率在2～3 kHz之间，在该频率附近磁场传感器具有最佳的磁场接收效果，解决了天然磁场信号在该频率处出现局部最小值给检测带来的困难，满足前面提出的设计要求。

本设计中反馈电阻Rfb=2.4 kΩ，反馈线圈的匝数N=30匝。图6所示为经反馈和低频频率补偿后，感应线圈的频率响应曲线。从图6可以看出，在1 Hz～9.8 kHz的频带范围内，线圈的响应曲线非常平坦，平坦度达±1.5 dB。但是，在10 kHz处出现小尖峰和频率响应曲线剧降的现象，这是由反馈线圈产生的二次谐振引起的。而在图5和图6中线圈的频率响应曲线在10 Hz和100 Hz之间出现的尖峰是由50 Hz的工频干扰引起的。

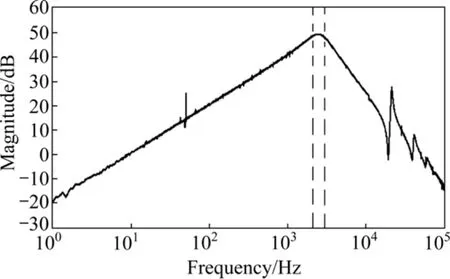
图5 没有前置放大器的线圈频率响应Fig. 5 Frequency response of search coil without preamplifier

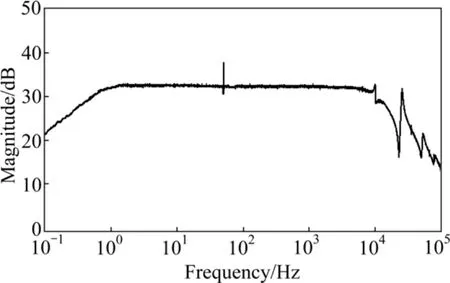
图6 经过电路调理后线圈频率响应Fig. 6 Frequency response of search coil with preamplifier

采用通电螺旋线圈产生标准磁场对传感器进行灵敏度标定。给螺旋线圈串联一个阻值为1 Ω的采样电阻并通入标准正弦信号，测试每个频点下传感器的输出电压幅值和采样电阻两端的电压幅值。通过采样电阻两端的电压幅值就可换算流过螺旋线圈的电流，并进一步计算得到螺旋线圈产生的磁场强度值，从而可得到在该频率下磁场传感器的灵敏度值。整个测试过程在一个经过电磁屏蔽的空间内进行。图7所示为本次设计的磁场传感器灵敏度—频率曲线。在1 Hz～9.8 kHz频带范围内传感器的灵敏度不随频率变化，幅值为40 mV/nT；在0.01～1 Hz频带范围内，传感器灵敏度正比于频率，当频率为0.1 Hz时，传感器的灵敏度为10 mV/nT。而受反馈线圈二次谐振的影响，在10 kHz处，传感器的灵敏度值先出现小尖峰然后急剧下降。

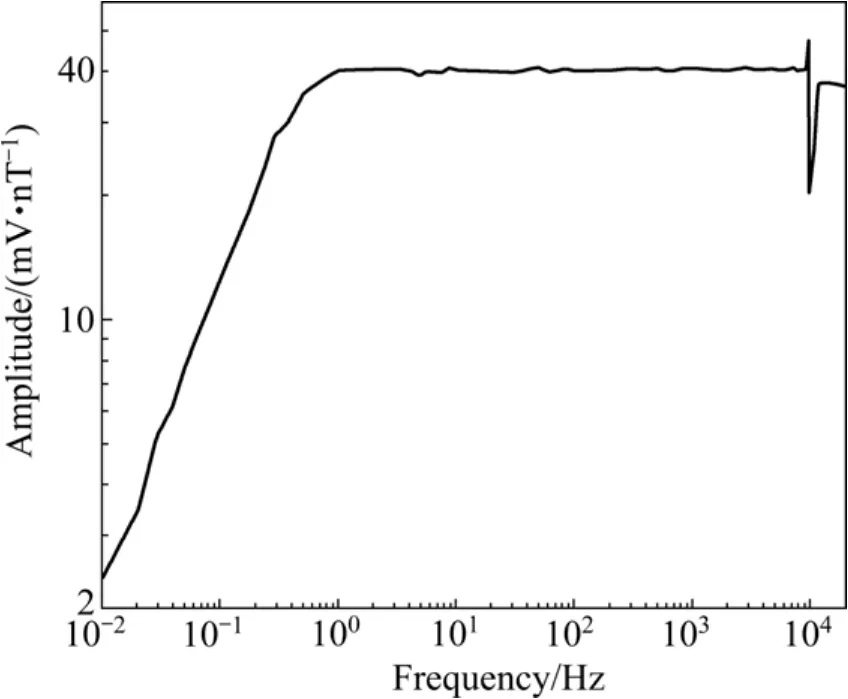
图7 磁场传感器灵敏度—频率曲线Fig. 7 Amplitude—frequency response curve of magnetic sensor

5 结论

1) 在分析磁芯和线圈结构对传感器灵敏度影响的基础上，并结合天然电磁场音频段磁分量的信号特征，设计磁场传感器谐振频率在2～3 kHz之间，使在音频段天然磁场信号局部最小值处具有最佳的磁场接收效果。

2) 采用磁通负反馈原理和对磁场传感器进行了低频电路补偿，扩展了频带，得到了在1 Hz～9.8 kHz频带范围内平坦度为±1.5 dB的灵敏度曲线，满足音频大地电磁探测的需要。

[1] 罗延中, 万 乐. 电法勘探新进展[M]. 北京: 地质出版社,1999: 28−46.

LUO Yan-zhong, WAN Le. New progress of electrical prospecting [M]. Beijing: Geological Publishing House, 1999:28−46.

[2] KAUFMAN A A, KELLER G V. 大地电磁测深法[M]. 刘国栋,晋光文, 邓前辉, 赵国泽, 王宝钧, 孙 浩, 译. 北京: 地震出版社, 1987: 1−40.

KAUFMAN A A, KELLER G V. The magnetotelluric sounding method [M]. LIU Guo-dong, JIN Guang-wen, DENG Qian-hui,ZHAO Guo-zhe, WANG Bao-jun, SUN Hao, transl. Beijing:Earthquake Publishing House, 1987: 1−40.

[3] 陈文华, 吴明启. 音频大地电磁仪中磁传感器的设计和研究[J]. 河北地院学报, 1982(12): 14−26.

CHEN Wen-hua, WU Ming-qi. Design and research of magnetic sensor in Audio-frequency magnetotelluric sounding [J]. Journal of Hebei University of Geological, 1982(12): 14−26.

[4] LENZ J E. A review of magnetic sensors [J]. Proceedings of the IEEE, 1990, 78: 973−989.

[5] 邵英秋. 感应式磁传感器线圈参数及其接口电路的研究[D].长春: 吉林大学, 2008: 1−3.

SHAO Ying-qiu. Magnetic induction sensor parameter of loop and study of its interface circuit [D]. Changchun: Jilin University,2008: 1−3.

[6] SEARN H C, FERGEAU P. An optimized low-frequency three-axis search coil magnetometer for space research [J].Review of Scientific Instruments, 2005, 76: 1−10.

[7] 张秀成. 大地电磁测深测量及仪器[M]. 北京: 地质出版社,1989: 23−42.ZHANG Xiu-cheng. Magnetotelluric measurement instrumentation[M]. Beijing: Geological Publishing House, 1989: 23−42.

[8] 耿胜利. GCI-1A型磁感应传感器的铁芯工艺研究[J].仪表技术与传感器, 1988(5): 21−25.

GENG Sheng-li. Research on ferromagnetic core of GCI-1A magnetic induction sensor [J]. Instrument Technique and Sensor,1988(5): 21−25.

[9] RIPKA P. Magnetic sensors and magnetometer [M]. Norwood:Artech House, 2001: 57−65.

[10] BOZORTH R M, CHAPIN D M. Demagnetizing factor of rods[J]. Journal of Applied Physics, 1942, 3: 320−326.

[11] PAPERNO E, GROSZ A. A miniature and ultralow power search coil optimized for a 20 mHz to 2 kHz frequency range [J].Journal of Applied of Physics, 2009, 105(7): 1−3.

[12] BOLL R, OVERSHOTT K J. Magnetic field sensors—Induction coil (search coil) sensors [M].VCH Publishers, 1989: 205−254.

[13] TUMANSKI S. Induction coil sensors—A review [J].Measurement Science and Technology, 2007, 18: R31−R46.

[14] 王言章, 程德福, 王 君, 林 君. 基于纳米晶合金的宽频差分式磁场传感器的研制[J]. 传感技术学报, 2007, 20(9):1967−1969.

WANG Yan-zhang, CHEN De-fu, WANG Jun, LIN Jun.Research of broad frequency difference magnetic field sensor based on nanocrystalline alloy [J]. Chinese Journal of Sensors and Actuators, 2007, 20(9): 1967−1969.

[15] 邵英秋, 程德福, 王言章, 张 飞. 基于磁反馈的宽频带磁传感器的研制[J]. 仪器仪表学报, 2010, 31(11): 2461−2466.

SHAO Ying-Qiu, CHEN De-fu, WANG Yan-zhang, ZHANG Fei.Development of broad frequency band magnetic field sensor based on flux feedback [J]. Chinese Journal of Scientific Instrument, 2010, 31(11): 2461−2466.

[16] 林继鹏, 王 君, 凌振宝, 程德福. 基于非晶态合金的感应式磁敏传感器的研究[J]. 仪器仪表学报, 2004, 25(2): 195−198.

LIN Ji-peng, WANG Jun, LING Zhen-bao, CHEN De-fu.Research for induction magnetic sensor based on amorphous alloy [J]. Chinese Journal of Scientific Instrument, 2004, 25(2):195−198.