随机分布树状分叉网络渗流特性的分形研究

王世芳，吴 涛，邓永菊，戴 伟

（1.湖北第二师范学院 物理与电子信息学院，武汉 430205；2.武汉工程大学 理学院，武汉 430074）

随机分布树状分叉网络渗流特性的分形研究

王世芳1＊，吴 涛2，邓永菊1，戴 伟1

（1.湖北第二师范学院 物理与电子信息学院，武汉 430205；2.武汉工程大学 理学院，武汉 430074）

基于Darcy定律和Hagen－Poiseuille方程，应用分形理论研究了母管直径分布具有分形分布的树状分叉网络的渗流特性，得到了具有随机分布的树状分叉网络渗透率的解析表达式.研究结果表明：通过具有随机分布的树状分叉网络的流量与压力梯度之间呈线性变化关系；其渗透率随分形维数Df和孔隙率φ的增加而增加，随长度比的增加而减小.

树状分叉网络；渗透率；Darcy定律；压力梯度

树状分叉网络是自然界一种常见网络结构，在生物工程、石油开采工程、材料科学工程、微电子器件冷却系统工程等实际应用领域得到了广泛的应用，因此树状分叉网络输运特性的研究引起众多学者的关注［1-5］.

树状分叉网络的研究始于1926年生理学家Murray对于血管系统血液流动优化管道直径比为2－1／3的提出［6-7］.Chen等人［8］提出了一个三维树状网络结构微通道散热器热流体动力学模型，他们的研究结果表明树状网络的微通道散热器在散热和压降损失等方面将比传统结构具有更大的优势.Xu和 Yu［9-10］采用两种不同的方法研究了“点到线”型和“点到圆”型树状分叉网络的渗流特性，还讨论了迂曲度对网络渗流特性的影响，但他们只研究了单个树状分叉网络渗流特性.Wang和Yu［11］研究了非牛顿幂律流体在单个Y－Shape树状分叉网络中的渗流特性，分析了网络结构参数对渗透率的影响.Li和Yu［12］研究非牛顿Bingham流体在单个规则树状分叉网络中启动压力梯度，讨论了网络微结构参数对启动压力梯度的影响.然而自然界中的分叉网络一般都是不规则的，且大部分是随机分布，仅仅用规则的树状分叉网络来分析渗流特性往往是不够的.本文以低渗透油藏中可能存在的裂缝网络为研究背景，将母管直径分布具有分形分布的“点到线”型树状分叉网络嵌入到多孔介质母体材料中，形成复合材料.假设这些分叉网络在分叉过程中没有重叠现象，分叉网络具有相同的直径比和长度比.为了研究问题的方便，本文忽略了母体介质对渗流的影响，主要研究了母管直径具有分形分布树状分叉网络的渗流特性.

1 母管直径具有分形分布的树状分叉网络的流量

单个类分形树状分叉网络一般是由初级到末级组成，设其最大分叉级数为m，每个母分支可以分成n个子分叉.图1是单个“点到线”型树状分形分叉网络的结构示意图［13］，第k级分叉的长度和直径分别为lk和dk，分叉角度为θ，为了描述分叉网络的几何结构，定义尺度因子γk和βk分别表示相邻两级分叉子管的长度比和直径比：

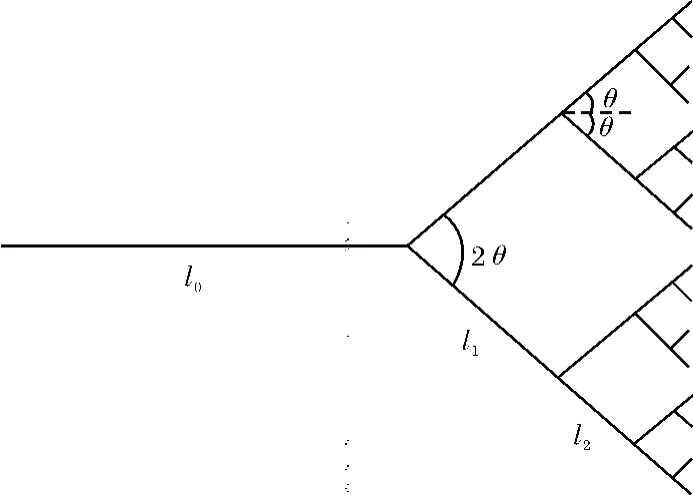
图1 点到线型树状分叉网络示意图［13］Fig.1 Fractal－like tree network model between apoint and a straight line［13］

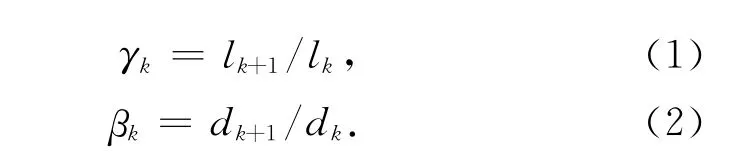
如果单个树状分叉网络具有分形特征，必须要求分叉长度比与直径比保持常数［1］，即：γk＝γ和βk＝β.第k级分叉管道的总数为nk，其长度与直径分别为［1］：

式中，l0和d0分别表示第0级管道的长度和直径.对于二分叉网络结构，分叉数n＝2.

图2 随机分布的类分形树状分叉网络嵌入到母体多孔介质中（忽略母体渗流的影响）Fig.2 A porous matrix embedded with randomly distributed Y－shaped fractal－like tree networks（The seepage of matrix is ignored）

图2为母管直径具有分形分布的树状分叉网络嵌入到母体多孔介质中形成复合介质示意图，这里忽略了母体的渗流影响.根据Hagen－Poiseuille方程，通过第k级分叉单管的流量为

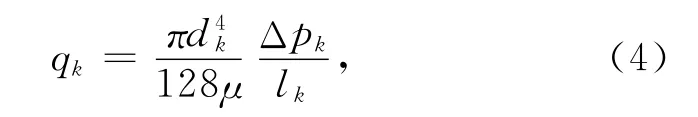
式中，Δpk为第k级单管两端的压强差，μ为牛顿流体的粘度.由（4）式可以得到流过第k级所有分叉管道的流量：

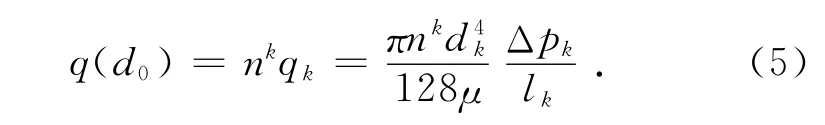
根据流体的质量守恒定律，第k级分叉网络的流量q（d0）也是通过单个树状分形分叉网络的总流量.由（5）式可得第k级分叉网络两端的压强降为：

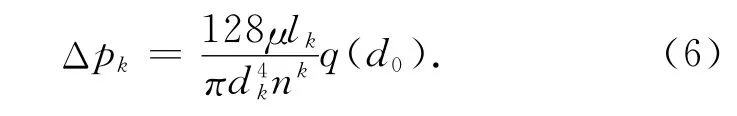
如果忽略网络分叉处的局部损失，网络的总压降Δp可近似等于各级压降Δpk之和：

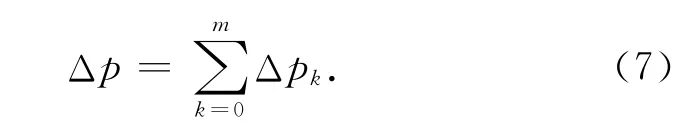
将方程（3）、（5）和（6）代入（7）式，得到分叉网络的总压降为：

根据方程（8），则流过母管直径为d0的单个分叉网络的流量重新改写为：

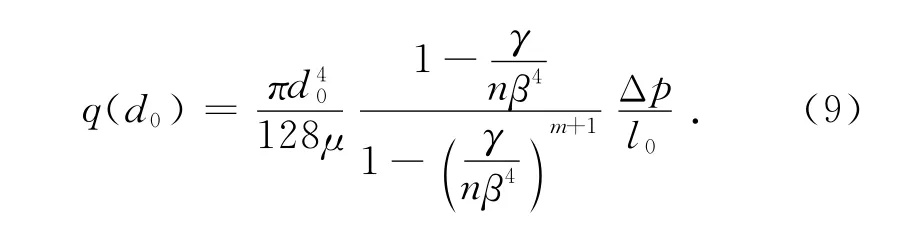
假设分叉网络的母管直径满足分形分布，则母管道直径分布在d0和d0＋d（d0）区间内的母管数目为：

根据Darcy定律：

式中，A和L0分别代表复合材料的横截面积和直线距离长度，L0可以由下式计算得［9］

将方程（11）（13）代入（12）式，得到随机分布的树状分叉网络嵌入到母体介质形成的复合介质的渗透率的分形解析表达式：

对于二分叉网络（n＝2），在保证分叉网络横截面积守恒的前提下，即每一个母管分叉出两个相邻子管道的横截面积均相等，得到直径比大小为

类似于多孔介质孔隙率的定义［14］，定义母管直径具有分形分布的树状分叉网络镶嵌到多孔介质中形成复合材料的孔隙率：

由上式可以看出复合材料无量纲渗透率k＋是分叉管道长度比γ、分叉角θ以及孔隙率φ和分形维数Df的函数，该表达式不含任何经验常数，清楚地揭示了影响裂缝网络渗透率的物理机制.

由此可以看出流量和渗透率对最大母管直径非常敏感.当m＝0或γ＝0时，每个树状分形分叉网络只有第0级单管，此时裂缝网络相当于由一束独立的、不同大小尺寸的平行直圆毛细管组成的，此时裂缝网络流量和渗透率的表达式与Yu和Cheng［15］给出的结论一致.

图3显示了基于方程（19）在不同最大母管直径下，通过裂缝网络的流量与压力梯度之间的关系.在总分叉级数m＝10、分叉角θ＝、分形维数Df＝1.1、孔隙率φ＝0.4、粘度μ＝1Pa·s下，通过裂缝网络的流量随压力梯度的增加而线性增加；当长度比γ＝0.6和直径比β＝时，分叉网络的最大母管直径越大，通过具有分形分布树状分叉网络的流量也越大.

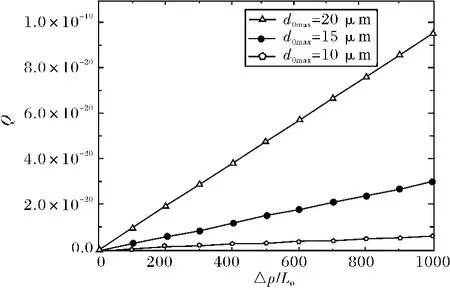
图3 在不同最大母管直径下流量与压力梯度之间的关系Fig.3 The flow rate versus the pressure gradient at the different maximum diameter of the 0th branching level

图4显示裂缝网络无量纲渗透率随孔隙率的变化趋势曲线.在m＝10，n＝2，θ＝，μ＝1Pa·s，γ＝0.6，β＝和Df＝1.1时，裂缝网络无量纲渗透率随孔隙率的增加而逐渐增加，这也与物理事实相符合.

图4 无量纲渗透率与孔隙率的关系曲线Fig.4 The dimensionless permeability versus the porosity

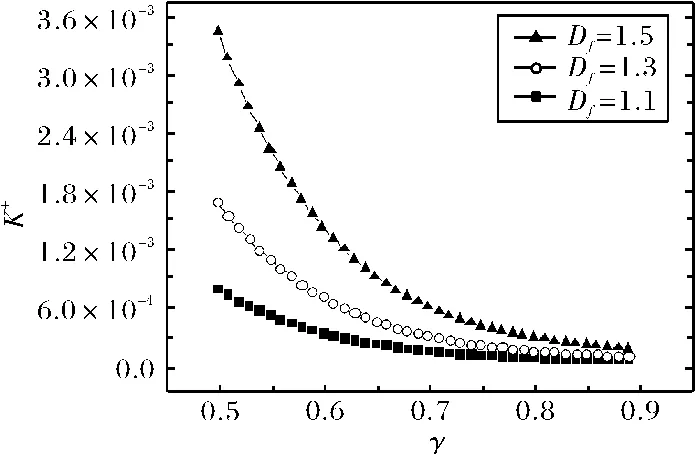
图5 在不同的分形维数下，裂缝网络无量纲渗透率随长度比的变化趋势图Fig.5 The dimensionless permeability versus the length ratio

图5显示了裂缝网络无量纲渗透率随长度比的变化趋势图，其中参数为m＝10，n＝2，θ＝π／4，β＝从该图可以看出，无量纲渗透率随长度比的增加而减小，最后逐渐趋近于0，这是因为流体流动阻力随着长度的增加而增加.

2 结论

本文基于分形理论与技术，将母管直径具有分形分布的树状分叉网络嵌入到母体材料中形成复合材料，在不考虑母体材料的渗透率情况下，得到了通过裂缝网络的流量以及渗透率的分形表达式.结果表明通过裂缝网络的流量与渗透率均对最大母管直径很敏感.裂缝网络渗透率k＋是最大母管直径d0max、长度比γ以及孔隙率φ和分形维数Df的函数，不含任何经验常数；且渗透率随分形维数Df和孔隙率φ的增加而增加，随长度比的增加而减小.

［1］Mandelbrot B B.The Fractal Geometry of Nature［M］.New York：Freeman，1982.

［2］McCulloh K A，Sperry J S，Adler F R.Water transport in plants obeys Murray's law［J］.Nature，2003，421：939－942.

［3］Mathieu－Potvin F，Gosselin L.Optimal conduction pathways for cooling a heat－generating body：A comparison exercise［J］.International Journal of Heat and Mass Transfer，2007，50：2996－3006.

［4］Lasance C，Simons R E.Advances in high－performance cooling for electronics［J］.Electronics Cooling，2005，11：22－38.

［5］Frey U，Hislop A，Silverman M.Branching properties of the pulmonary arterial tree during pre－and postnatal development［J］.Respiratory Physiology ＆ Neurobiology，2004，139：179－189.

［6］Murray C D.The physiological principle of minimum work.I.The vascular system and the cost of blood volume［J］.Proc Natl Acad Sci U S A，1926，12：207－214.

［7］Murray C D.The physiological principle of minimum work applied to the angle of branching of arteries［J］.J Gen Physiol，1926，9：835－841.

［8］Chen Y P，Chen B Z，Shi M H，et al.Thermal and hydrodynamic characteristics of constructor tree－shaped minichannel heat Sink［J］.AIChE，2010，56：2018－2029.

［9］Xu P，Yu B M，Feng Y J，et al.Analysis of permeability for the fractal－like tree network by parallel and series models［J］.Physica A，2006，369：884－894.

［10］Xu P，Yu B M，Feng Y J，et al.Permeability of the fractal disk－shaped branched network with tortuosity effect［J］.Phys Fluids，2006，18：078103－078104.

［11］Wang Shifang，Yu Boming.Analysis of seepage for powerlaw fluids in the fractal－like tree network［J］.Transp Porous Media，2011，85：191－206.

［12］Li Yan，Yu Boming.Study of the starting pressure gradient in branching network［J］.Sci China Tech Sci，2010，53（9）：2397－2403.

［13］Lorente S，Wechsatol W，Bejan A.Tree－shaped flow structures designed by minimizing path lengths［J］.Int J Heat Mass Transfer，2002，45：3299－3312.

［14］Meijuan Yun，Boming Yu，Jianchao Cai.A fractal model for the starting pressure gradient for Bingham fluids in porous media ［J］.International Journal of Heat and Mass Transfer，2008，51：1402－1408.

［15］Yu Boming.Fractal analysis of permeabilities for porous media［J］.AI Ch E J，2004，50：46－57.

Analysis on seepage of the randomly distributed fractal－like tree network

WANG Shifang1，WU Tao2，DENG Yongju1，DAI Wei1
（1.School Physics and Electronic Information，Hubei University of Education，Wuhan 430205；2.School of Science，Wuhan Institute of Technology，Wuhan 430074）

Based on Darcy's law and Hagen－Poiseuille equation，the flow characteristics of the randomly distributed fractal－like tree network with the diameter d0of the 0th branching level are investigated by use of fractal theory，which follows the fractal scaling law.An analytical expression for permeability of the randomly distributed fractal－like tree network is presented.The results show that the flow rate for the randomly distributed fractal－like tree network scales linearly with pressure gradient.The dimensionless permeability for the randomly distributed fractal－like tree network increases with the increase of fractal dimension and porosity and decreases with the increase of the length ratio.

fractal－like tree network；permeability；Darcy law；pressure gradient

O357

A

1000－1190（2012）04－0406－04

2011－12－05.

湖北省教育厅科学技术项目（B20113002）.

＊E－mail：flatime＠sina.com.