装备健康状态评估方法研究*

姚云峰，伍逸夫，冯玉光，赵建印

(1．海军航空工程学院，山东 烟台 264001;2．海装驻武汉地区军事代表局，湖北 武汉 430022)

0 引言

由于视情维修的前提就是依据装备当前的健康状况来决定是否维修以及采用何种维修保障方式，因此评估装备当前的健康状态，确定其健康状态退化情况，对于实现装备的视情维修具有重要意义。对于武器装备，由于环境应力对其健康状态的影响无法精确确定，即装备的健康状态主要是由通电测试得到的参数的测试数据来表征的。在忽略测试设备误差的情况下，参数的测试数据是装备健康状态的最直接反映，因此可以应用参数的测试数据对装备测试时的健康状态进行评估。

1 装备健康状态的内涵

1．1 装备健康状态基本概念

对装备进行健康状态评估之前，需要明确装备健康状态的概念。根据文献［1］，装备的健康状态描述了装备及其部件执行设计功能的能力。由此可见，健康状态表征的是一种能力。由于装备的健康状态一般是通过测试数据来表征的，测试数据偏离标准值的程度越大，其健康状态越差，因此装备的健康状态在一定程度上可表现为测试数据偏离标准值的程度。

通过对装备健康状态的定义与可靠性定义的对比可以发现，它与可靠性的区别主要体现在“稳定”和“持续”上［2］。从某种程度上说，装备的健康状态是指装备保持一定可靠性水平的能力，是装备在使用状态下可靠度保持在一定范围(保证装备完成预定功能的前提下)的置信水平。保持一定的可靠性水平是指在今后较长一段时间内装备能正常工作［2］。

1．2 装备健康状态等级分类

以往对装备进行健康状态评价时，往往采用“是非制”，即将其健康状态简单地划分为合格和不合格，认为测试数据落在规定的阈值范围内是合理的，超出规定的阈值是不合格的。这种“是非制”的评估方法对于状态非常良好的装备和状态已经接近故障的装备可能会采用相同的维修策略，这对于前者将产生不必要的维修，而对于后者可能会因维修不足而影响其战备完好性，无法实现装备的视情维修，因此考虑将装备的健康状态等级细化［3－4］。但是健康状态等级的分类也不能过多，否则对于不同健康状态等级的装备，可能会无法判断采取何种维护保障措施。为了更好地描述装备的健康状态，本文从健康管理的角度出发，根据装备测试数据偏离标准值的程度，建议将装备的健康状态分为优、良、中、差和故障5个等级，如表1所示。

根据以上定义，可以认为优状态和良状态属于健康，中状态和差状态属于亚健康。处于“健康”和“亚健康”状态的装备，由于所有参数的测试数据均在允许范围内，因此是合格的。但是对于“亚健康”的装备，要引起维修保障人员的注意，在未来一定时间内，这种状态的装备很可能会退化为故障状态，因此必须加强监测。对于故障状态的装备，由于参数的测试数据超过阈值，因此是不合格的，为保证其战备完好性和任务成功性，必须立即安排合理的维修保障措施。

表1 健康状态分级及等级描述Table 1 Classification of health condition and description

由于现行的装备故障与否的判断准则是通过测试数据来表征的，如果测试数据超过阈值，就可以判定装备故障。因此对于装备的故障状态等级，可以根据测试数据是否超过阈值来判断。而装备的优、良、中、差健康状态等级之间则没有明确的界限划分，只有模糊的过渡区域［3］。比如说，处于优—良状态边缘的装备可能既隶属于优状态，也隶属于良状态，只是隶属于2种健康状态的隶属度不同，这时就需要依据一定的方法对装备的健康状态进行决策，确定其最终健康状态等级，以便于根据评估结果及时安排维修、排除安全隐患［5］。

2 装备参数健康状态评估

由于装备的健康状态是由多个参数的健康状态综合表征的，因此为了确定装备的健康状态，需要对其参数进行健康状态评估，确定各个参数的健康状态。由装备的健康状态等级分类可知，对装备的参数进行健康状态评估时，首先应根据参数的测试结果判断参数是否超差。如果参数的测试结果超过阈值，表明参数是不合格的，此时可以直接判定装备处于故障状态。反之则表明参数是合格的，需要对其进一步分析。下面对测试合格的参数进行健康状态评估，在不加说明的情况下本节中的参数均指测试合格的参数。

2．1 参数健康状态的归一量化

对参数的测试结果进行分析时，由于参数的技术要求大多不相同，因此得到的表征参数健康状态的测试数据偏离标准值的程度也大多不同，为使不同参数之间的健康状态具有可比性，可考虑对参数的测试数据进行归一化处理，用测试数据的归一化值来表征参数的健康状态。对测试数据进行归一化时，可以设定测试数据偏离标准值的程度越大，其归一化值越小，这样测试数据的归一化值在一定程度上也就表征了参数的健康状态，测试数据的归一化值越小，测试数据偏离标准值的程度越大，参数健康状态越差。

假设装备有n个参数，第i(i=1，2，…，n)个参数的测试结果为xi，标准值为xs，上阈值为xu，下阈值为 xl，则本次测试值与标准值的偏差 Δ=，参数的上最大允许误差δ1=，下最大允许误差δ2=，参数的归一化值λi可定义为

由式(1)可知，当参数的测试结果为标准值时，其归一化值为1，表示参数的健康状态最好;随着测试数据偏离标准值的程度变大，其归一化值变小，参数的健康状态变差;当参数的测试结果达到阈值，其归一化值为0，表明参数的健康状态最差。

2．2 参数健康状态等级的隶属度

由装备的健康状态等级分类可知，装备的优、良、中、差健康状态具有模糊性，即由于缺乏从一种健康状态等级到另一种健康状态等级的明显过渡而引起的不确定性，这种不确定性是非随机的，可以用模糊集合理论来表示［6］。

模糊集合的思想是把经典集合中的绝对隶属关系模糊化，使元素对集合的隶属程度不再局限于取0或1，而是可以取区间［0，1］上的任一数值，这一数值反映了元素隶属于集合的程度［7］。

根据文献［7］，模糊集合完全可以由其隶属度函数来刻画。对于任意x∈X，都有唯一的隶属度函数 μA～(x)∈［0，1］与之对应。μA～(x)的值接近 1，表示 x 隶属于A～的程度很高;μA～(x)的值接近于0，表示x隶属于A～的程度很低。常见的隶属度函数有正态型、柯西型、三角型和降Γ分布等。

对于装备而言，其全部参数的集合可看作论域X，优、良、中、差健康状态等级可分别看作模糊集合A～i(i=1，2，3，4)。因此装备任一参数可用隶属度函数来表述它与优、良、中、差健康状态等级之间的从属关系。由于测试数据的归一化值是对参数健康状态表征，因此可以根据测试数据的归一化值来确定参数的隶属度函数。同时，由于三角型隶属度函数形状简单，并且与其他较复杂的隶属度函数得出的结果差别较小［8］，因此本文采用三角型隶属度函数，根据装备健康状态退化的实际情况和专家经验，可得装备参数的三角型隶属度函数如图1所示。

图1 参数的三角型隶属度函数Fig．1 Triangle membership function of parameter

从图1中可以看出，根据三角型隶属度函数，每一个参数都隶属于2个相邻的健康状态等级，即装备参数的健康状态可能隶属于相邻2个健康状态等级中的任何一个，只是其隶属度可能不同，且装备隶属于相邻2个健康状态等级的隶属度之和为1。

2．3 参数的权重

权重是表征评估指标重要程度大小的度量，要准确评估装备的健康状态，需要确定各参数的权重。由于测试数据的归一化值表征了参数的健康状态，归一化值越小说明参数偏离标准值的程度越大，其健康状态越差。因此对装备进行健康状态评估时，应将健康状态较差的少数参数突出出来，即参数的健康状态越差，其归一化值越小，权重应该越大。为了根据参数的健康状态确定权重，可以对每一个参数的归一化值取倒数，将得到的结果除以全体参数归一化值的倒数和，即可得到每一个参数的客观权重。

设装备有n个参数，第i(i=1，2，…，n)个参数的归一化值为λi，则该参数的权重可表示为

由式(2)可知，参数的归一化值越小，其权重越大;当某一个参数的归一化值为0时，说明该参数的测试结果达到了规定的阈值，此时该参数的权重为1，而其他参数的权重则为0，可以直接根据该参数的健康状态来判断装备的健康状态，这与实际情况是相符的。

3 基于改进证据理论的装备健康状态评估模型

由于装备的健康状态是由多个参数的健康状态综合表征的，因此对参数进行健康状态评估，确定其健康状态之后，可以根据参数的健康状态来确定装备的健康状态。根据参数的健康状态评估结果，如果一个或多个参数处于故障状态，则可以直接判定该装备为故障状态;如果所有参数的健康状态均合格，则表明装备是合格的，此时每一个参数的健康状态都表征了装备相应部件的健康状态，对装备进行健康状态评估实际上是一个多属性的决策问题，可以考虑对这些参数的健康状态进行融合以达到目标属性判决的目的。由于测试不合格的装备的健康状态已经确定，因此本节仅对测试合格的装备进行健康状态评估。

3．1 装备健康状态评估的改进证据理论

D-S组合规则是证据理论的核心，它可以有效地将来自不同信息源的独立证据信息进行融合，具有较强的决策处理能力［9］。

由于装备的优、良、中、差健康状态等级可以构成测试合格的装备健康状态评估的识别框架，且根据装备参数的三角型隶属度函数，各参数隶属于优、良、中、差健康状态等级的隶属度满足基本概率赋值函数的定义，因此装备参数隶属于优、良、中、差健康状态等级的隶属度即为其基本概率赋值。

应用D-S组合规则对装备多个参数的健康状态进行合成时，证据理论的合成公式认为所有参数提供的证据在合成过程中的重要程度是一样的。实际上，随着某一两项参数健康状态的严重恶化，装备的综合健康状态也急剧下降，即装备的健康状态受少数健康状态较差的参数的影响较大，各个参数提供的证据在证据合成过程中的重要程度是不一样的，因此有必要在证据合成过程中引入可描述证据重要程度的权重系数，其方法如下［10－11］。

(1)根据证据源提供的证据确定识别框架内各命题的基本概率赋值，并建立证据源的权重向量

(2)设 wmax=max(w1，w2，…，wn)，可得相对权重向量 w*=(w1，w2，…，wn)/wmax，由此可以确定证据基本概率赋值的“折扣率”利用“折扣率”对识别框架内所有命题的基本概率赋值进行调整，调整后的基本概率赋值为

式中:k=1，2，…，di，di为第 i个证据提供的识别框架内的非U焦元数。

由此可见，调整后的基本概率赋值函数不满足和为1的条件，为构成基本概率赋值函数需要补充定义

于是由式(4)和(5)定义的函数可构成一个新的基本概率赋值函数［12］。确定各参数新的基本概率赋值之后，由于各参数之间独立不相关，因此可应用D-S组合规则对装备参数的健康状态进行合成。

3.2 装备健康状态等级的决策

应用改进证据理论对装备多个参数的健康状态进行合成之后，为了确定装备的最终健康状态等级，可以采用基于基本概率赋值的决策方法对装备多个参数的健康状态合成结果进行决策［9］。

设∃A1，A2⊂U为装备2个健康状态等级，满足

对于预先设定的门限 ε1，ε2，若式

成立，则认为判决结果为A1的可能性远大于A2，即装备的最终健康状态等级为A1。

3．3 评估模型的验证

应用基于改进证据理论的装备健康状态评估模型确定测试合格的装备的健康状态等级之后，可以采用纵向对比法对评估模型进行验证。

纵向对比法即根据装备的历史测试信息对装备历次测试时的健康状态进行评估。在不考虑对装备进行维护的情况下，装备的健康状态应是逐渐恶化的。如果评估模型合理，则装备历次测试时的健康状态应逐渐朝着状态恶化的方向发展。

4 实例分析

已知某装备的健康状态可由7个独立不相关的参数表征，且该装备已经测试6次，未经历任何维护，第6次测试时7个参数的测试结果均合格，为了确定该装备的健康状态退化情况，可以对第6次测试时的健康状态进行评估。

首先根据式(1)对7个测试合格的参数的测试数据进行归一化处理，可得其归一化值为0．36，0.60，0．80，0．90，0．88，0．62．由于测试数据的归一化值是对参数健康状态的表征，因此为了直观地表示装备7个参数的健康状态，可作一单位圆并对其7等分，得到7条半径。每条半径的长度为1，表示每个参数测试数据的最大归一化值1，这样每个参数测试数据的归一化值λi可表示为第i条半径上的一个点，λi离圆心越近，说明测试数据的归一化值越小，参数的健康状态越差。将7个参数的归一化值在单位圆上连接起来，即可得到装备的多参数健康状态曲线，因其外形与雷达相似，故可称作多参数健康状态雷达图，如图2所示。

确定参数测试数据的归一化值之后，可以根据参数三角型隶属度函数确定参数隶属于优、良、中、差健康状态等级的隶属度，并应用式(2)确定参数的权重，结果如表2所示。

图2 多参数健康状态雷达图Fig．2 Health condition radar chart of parameters

表2 装备参数的健康状态评估结果Table 2 Health condition assessment result of parameters

确定7个参数隶属于优、良、中、差健康状态等级的隶属度之后，为了直观地表示7个参数的健康状态，以便于分析潜在的故障，可作参数健康状态映射图如图3所示。

图3 参数健康状态映射图Fig．3 Health condition mapping chart of parameters

图中每一个六边形代表一个参数，青色部分代表该参数隶属于优状态，黄色部分表示该参数隶属于良状态，橘红色部分表示参数隶属于中状态。从图中可以看出每个参数都隶属于2个健康状态等级，即参数的健康状态具有模糊性。

确定参数的隶属度，即其基本概率赋值之后，可知第2个参数的权重最大，因此可以将其他参数的权重除以第2个参数的权重以确定其“折扣率”，进而根据式(4)和(5)确定参数修改后的基本概率赋值如表3所示。

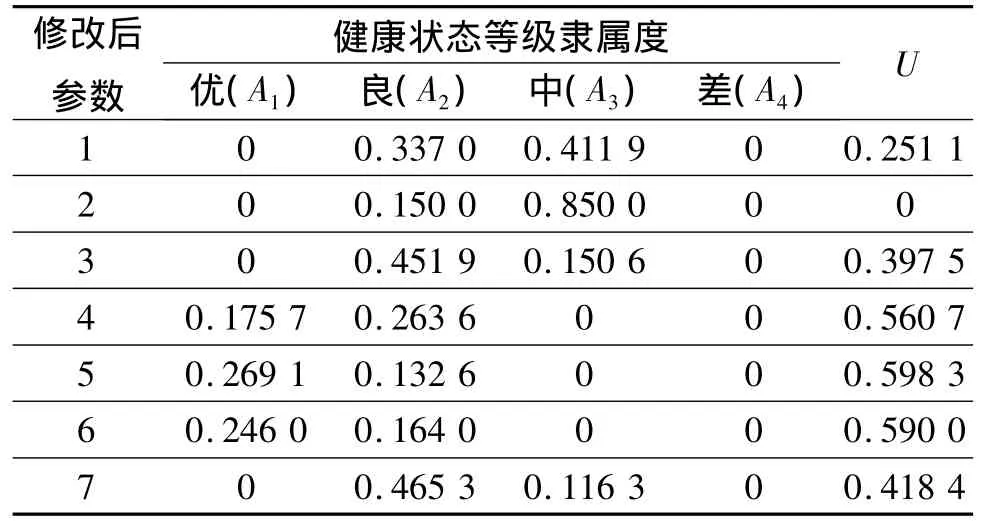
表3 参数修改后的基本概率赋值Table 3 Basic probability assessment of revised parameters

应用证据合成规则对表3中的基本概率赋值进行合成，可得合成结果为 m(A1)=0，m(A2)=0.479 2，m(A3)=0．520 8，m(A4)=0，m(U)=0。如果取阈值ε1=ε2=0.01，则根据式(8)可知判决结果为A3，即该装备的最终健康状态为中状态。

同理对该装备前5次的测试结果进行健康状态评估，可知其评估结果为优，良，良，良，良。由于该装备的健康状态是平稳变差的，因此本文建立的评估模型是合理的。

5 结束语

本文首先对装备健康状态的内涵进行分析，将装备的健康状态分为优、良、中、差和故障5个等级，认为处于优、良、中、差状态的装备是合格的，其健康状态具有模糊性，而处于故障状态装备则是不合格。其次对装备参数的健康状态进行评估，根据测试数据确定测试合格的参数健康状态的归一化值，进而根据归一化值确定参数健康状态等级的隶属度及其权重。最后根据参数的健康状态评估结果对装备进行健康状态评估。对于测试不合格的装备，可以直接判定其处于故障状态;对于测试合格的装备则建立基于改进证据理论的装备健康状态评估模型，根据参数的权重对原始证据源修改，进而应用D-S组合对参数的健康状态进行融合并决策，确定装备的最终健康状态等级，并进行实例分析，验证了评估模型的合理性。

［1］ FERREL B L．Air Vehicle Prognostics＆ Health Management［C］∥Proceedings of IEEE Aerospace Conference，New York:IEEE，2006:145－146．

［2］ 余鹏，吕建伟，刘中华．舰船装备健康状态评估及其应用研究［J］．中国修船，2010，23(6):47－49．

［3］ 王俨凯，廖明夫．航空发动机健康等级综合评价方法研究［J］．航空动力学报，2008，23(5):939－942．

［4］ 吴波，贾希胜，夏良华．基于模糊聚类和综合评判的装备－装备群健康状态评估［J］．军械工程学院学报，2009，21(5):1－5．

［5］ 韩国泰．航空电子的故障预测与健康管理技术［J］．航空电子技术，2009，40(1):30－38．

［6］ 郭利，张锡恩，马彦恒．模糊数据融合算法在设备监测中的应用［J］．传感器技术，2004，23(6):73－74．

［7］ 杨伦标，高英仪．模糊数学原理及应用［M］．广州:华南理工大学出版社，2005:62－65．

［8］ 廖瑞金，王谦，骆思佳，等．基于模糊综合评判的电力变压器运行状态评估模型［J］．电力系统自动化，2008，32(3):71－73．

［9］ 何友，王国宏，关欣．信息融合理论及应用［M］．北京:电子工业出版社，2010:57－60．

［10］ 叶清，吴晓平，宋业新．基于权重系数与冲突概率重新分配的证据合成方法［J］．系统工程与电子技术，2006，28(7):1014－1016．

［11］ 朱承治，郭创新，辛建波．基于改进证据推理的变压器状态评估研究［J］．高电压技术，2008，34(11):2332－2336．

［12］ 郭华伟，施文康，刘清坤，等．一种新的证据组合规则［J］．上海交通大学学报，2006，40(11):1895－1900．