平等与效率关系的数理经济逻辑——基于完全自由竞争的前提

何晓星

（上海市发展改革研究院，上海 200032）

●理论经济学

平等与效率关系的数理经济逻辑
——基于完全自由竞争的前提

何晓星

（上海市发展改革研究院，上海 200032）

运用数理经济学理论方法可以建立平等与效率关系新的逻辑框架。假设平等、效率是两种消费品，弱者、强者是两种消费者。在强、弱两者关于平等、效率的纯交换经济中，在完全自由竞争的前提下，两者经过竞争交易和讨价还价博弈，有可能实现均衡。这种均衡只是在一定条件下的产物，其具有存在性的三个主要条件是，相应的平等与效率关系满足凸性、紧致性和连续性；其具有稳定性的三个主要条件是，上述关系满足总量可替代性、瓦尔拉斯律和齐次性。

完全自由竞争；平等；效率；均衡；存在性；稳定性

一、引言和文献简述

平等与效率的关系是一个重大问题。这个问题在实践中争议不休，主要原因是在理论上争议不休。尽管关于平等与效率关系的理论浩如烟海，但运用数理经济逻辑来分析这一问题的文献迄今比较鲜见。范里安·H（2009年，第507～508页）在一般商品的交易中，寻找其中体现的平等与效率；但他尚未将平等、效率作为消费品，即从这个角度来分析平等与效率的关系。丁烈云等（2006年，第44～47页）将平等、效率作为一对函数，以基尼系数代表平等作为因变量，以人均GDP代表效率作为自变量，从而以中国的宏观数据来实证研究平等与效率的关系。何大昌（2002年，第42～52页）研究了公平与效率两者均衡的存在性问题。他指出：经济学就是在机会集合范围内以替换形式分析成本问题的，一种选择的成本可用效率的损失来表示提高结果公平的成本；当边际收益等于边际成本时产生了均衡，可用边际社会成本等于边际社会收益来定义公平和效率的均衡，即最优组合。

虽然以上见解均有启发意义，但至今仍然缺乏运用系统的数理经济学理论，将平等、效率直接作为两种消费品，以此为对象，来研究不同消费者对平等、效率进行交易时如何达到均衡并实现稳定。而这正是本文试图解决的问题。鉴于平等、效率的定义、概念纷繁复杂，为减少歧义，笔者采用最简化最直观的也为大多数人凭直觉可以判断的定义：平等就是收入分配结果的平等，也即分配的无差别化、对称化或平均化，而衡量平等简言之就是观察切分蛋糕的平均化程度；效率就是在既定投入下产出最大化，衡量效率就是观察做大蛋糕的最优增长程度。一些数理经济方法也是类似这样定义的，如洛伦茨曲线描述的平等，最优反应函数和纳什均衡描述的效率等。在本文中主要研究平等与效率的关系，特别是这种关系的核心即竞争交易均衡，而非平等效率消费的本身。

笔者运用数理经济学理论方法，分析平等与效率关系的主要逻辑如下：平等和效率是两种消费品，弱者和强者是两个（种）消费者，强弱两者关于平等、效率的消费和竞争交易受到收入预算约束。在强弱两者的纯交换经济中，在完全自由竞争的前提下，假设满足一系列条件，那么经过两者关于平等、效率的交易和讨价还价博弈，则有：（1）强弱两者各自关于平等、效率消费的替代达到了最优；（2）强弱两者各自关于平等、效率的边际替代率达到彼此相等；（3）通过上述替代强弱两者各自的消费都实现了预算约束下的效用最大化；（4）总之，这表明强弱两者之间的交易和博弈达到了均衡。应指出，这种均衡既不是必然存在和稳定的，也不是必然不存在和不稳定的，而均衡的存在和稳定只是在一定条件下的产物。因而本文讨论的重点是，决定上述均衡具有存在性和稳定性，究竟需要哪些条件。当然，本文的主要任务是试图提出一个逻辑框架，并给出一些分析，而非正式地证明这个逻辑。

二、基本假设：平等与效率关系的数理经济逻辑

虽然运用数理经济学理论可以分析任何消费品，但如何将平等、效率作为具有自身特点的消费品，以它们的关系为研究对象，建立起数理经济分析的逻辑框架，却是本文的尝试。

（一）概念和前提

1.在完全自由竞争条件下的两人纯交换经济。为了讨论方便，笔者将平等与效率关系限定为“在完全自由竞争条件下的两人纯交换经济”。（1）两人：强者和弱者。从某种意义来说，全部人口可划分为上述两类消费群体。当然每类群体人口都是无限多，这里简化为两个消费者或交易者。同时这也表明“两人”不受外部性的影响。（2）纯交换经济：一是强弱两者分别成为交易双方，两者只有交换，没有生产函数，因此也不区分供方和需方；二是在交换中只是以物易物，没有货币，不存在利率、汇率、币值及通货膨胀、通货紧缩等有关问题；三是两者交换的只是两种特定的消费品：平等和效率。（3）完全自由竞争场所的前提。这个前提对于强弱两者关于平等、效率的交易能够达到均衡至关重要。高山晟（2009年，第166、280页）指出：根据价格做出的分散决策之间的协调，是竞争性均衡概念的本质所在；竞争均衡具有的唯一形式：分散化决策过程。这表明，分散化决策保证了没有垄断、完全自由的竞争，还保证了信息和物质流动的完全自由、公开，从而保证了经典经济学理论要求的自由竞争均衡的实现。

2.作为竞争交易对象的消费品：平等和效率；作为竞争交易主体的消费者：强者和弱者。两种消费品：设xi为平等，xj为效率。两者虽然是具有特定个性的消费品，但也具有一般商品的共性：（1）商品的可细分性（高山晟，2009年，第 157页）；（2）商品效用的可转移性（高山晟，2009年，第 174页）；（3）在纯交换经济中的“商品守恒”，商品既不会产生也不会消灭（埃里克森·B，2008年，第12页）。总之，这两种消费品构成了两维商品空间，即以xi为横轴、xj为纵轴的平面坐标系，这是消费者可以进行平等、效率替代交易的平台。

两个消费者：设a为弱者，b为强者。本文中的强弱者概念，只是以各自对于平等、效率消费品的不同偏好来区分。弱者的定义是“平等偏好者”，即有，这表示就弱者a来说，其偏好平等更甚于效率。强者的定义是“效率偏好者”，即有，这表示就强者b而言，偏好效率更甚于平等。应强调，本文中的强、弱只是就上述偏好意义来说的，不同于一般语言意义上的强弱者概念。

3.平等与效率的边际替代率。假设平等、效率可以相互替代，那么一个消费者在消费这两种消费品时，在取得同样效用下可以选择它们不同的消费组合。在这些组合中，可以是平等xi多些，而效率xj少些；也可以是效率xj多些，而平等xi少些。另一方面，平等效率的组合效用u=u（xi，xj）；那么在u=c（常数）条件下，xi，xj有任意不同的组合，故在不变的效用下，xi，xj可有不同的替代率。为比较变化的程度和速度，采用边际替代率这一形式。鉴于此，平等xi和效率xj构成不同的边际替代率。有边际替代率上式表明每个消费者各自的平等/效率边际替代率，等于该消费者分别对于平等以及效率消费的边际效用之比。同时平等xi与效率xj构成该消费者组合效用的无差异曲线，而边际替代率MRSi，j（x）=|dxj/dxi|就是该曲线斜率的绝对值。另一方面，消费品价格等于边际效用，因此无论对于弱者a还是强者b，［∂u（x）/∂xi］/［∂u（x）/∂xj］=Pi/Pj，而上式左边又等于MRSi，j（x）。可见，对于每一个消费者，平等与效率的价格之比Pi/Pj，即它们的相对价格，又等于它们的边际替代率。

4.平等与效率关系的预算约束。在资源稀缺、没有免费午餐的经济学公理之下，任何竞争交易只能在预算约束下进行。在纯交换经济中，预算约束就是初始禀赋约束；在引入生产、供给后，它就是收入约束，也可以说收入中包括初始禀赋。那么在纯交换经济中，强弱者之间的竞争交易，只能依据原有的初始禀赋，即原有的消费品平等xi和效率xj进行交易。在平面坐标图上显示，需求是选择集（偏好关系）与预算集可分离，但在均衡时又有共切点的产物。其含义是一个商品束属于消费者的消费集，当且仅当消费者能够付得起相应代价，并且也没有比这更好的其他商品来可供选择。换言之，每个消费者在预算集约束下最大化其效用（埃里克森·B，2008年，第12页）。这对于平等效率的交易也是如此，它们的预算集对消费集，也是两点：一是约束后者，二是支撑其效用最大化。

在坐标图上，预算集的右上方边界就是预算线；而预算线经过强者或弱者关于平等、效率之初始禀赋的那一点（xi0，xj0）。同时预算线的斜率为－（Y/Pj）/（Y/Pi）=-Pi/Pj，其中Y为平等效率共同被其约束的收入。可见预算线的斜率等于平等、效率相对价格的绝对值。另一方面，又因为平等、效率无差异曲线斜率的绝对值|dxj/dxi|=MRSi，j（x）=Pi/Pj，可见在均衡点，无差异曲线斜率同预算线斜率相等，并共一条切线。此外由于MRSi，j（x）=Pi/Pj，故可反过来说，当交易达到均衡时，平等与效率的相对价格，即预算线之斜率等于平等、效率的边际替代率。

（二）强弱两个消费者关于平等、效率的竞争交易

在交易前强弱两者各自拥有的平等、效率初始禀赋，按“掷钱币游戏”这种最普遍的随机方式界定：每个消费者（强者或弱者）各拥有50%概率之平等，50%概率之效率。假定以1为每个消费者拥有消费品的全部份额，那么，上述每个消费者都同样拥有0.5 的平等，记为 0.5xi；0.5 的效率，记为 0.5xj。

确定初始禀赋后的交易过程如下：由于强者更偏好效率，为增加效用，故拿一部分平等xi去换取弱者之效率xj。交易结果强者之效率增加了，有0.5xj；而平等减少了，有。另一方面，由于弱者更偏好平等，为增加效用，故拿一部分效率xj去换取强者之平等xi。交易结果弱者之平等增加了，有，而效率减少了，有。综上所述，首先对于每个消费者（强者或弱者），两者的相互交易和各自自身的替代同在而互不可缺，是同一件事情的两面。其次，由偏好发生的替代和交易都产生效用，即每个消费者自身产生了平等、效率的替代效用，从而产生了强弱两者之间的交易效用，否则竞争交易不能发生。

但强者并不能将自身替代和互相交易进行到极端，即达到效率xj为1而平等xi为0。因为一方面因旨在提高效率引起的自身替代和互相交易的边际效用递减；另一方面这种交易与替代是有成本的，事实上，强弱两者都不是孤立存在的，而是互相映射的，比如平等或不平等正是强弱两者比较的差距。其中强者受到来自弱者的嫉妒压力，因为如果强者的平等xib很少以至为零，意味着不平等极大，这当然引起弱者对强者嫉妒压力的增大，从而增加了两者的交易成本和强者自身的替代成本，这种成本随着不平等程度和嫉妒压力增大而增加。因而，当强者的交易替代效应小于其交易替代成本时，强者自身关于平等、效率的替代以及强弱者之间的交易停止。这时强者的

同样弱者也不能将自身替代和互相交易进行到极端，即达到平等xi为1而效率xj为零。因为一方面因旨在提高平等引起的替代和交易的边际效用递减；而另一方面替代和交易成本增加，这是由于弱者受到来自强者的嫉妒压力，因为平等极大意味着不平等极小，这使得强者对弱者的嫉妒压力增大，从而增加了两者的交易成本和弱者自身的替代成本，这表明同弱者产生嫉妒压力一样，强者也会产生嫉妒压力，只不过同弱者的方向相反。应指出嫉妒仅具有中性，并可广泛地解释为不满。

休谟·D（2007年，第103页）指出，成为嫉妒对象的快乐往往比我们所有的快乐占着优势：一方面，一种优势使我们相形见绌，并呈现出个人不愉快的比较来；另一方面，甚至就在他处于劣势的情况下，我们（笔者注：此处指强者）仍然希望同他有一种较大的距离，以便增大自我的观念；当这个距离减少时，那种比较对我们的利益要少些，因而使我们感到较小的快乐甚至不愉快；人们在看到比他地位低微的人在追求光荣或快乐方面接近或赶上他们时，就感觉到那种嫉妒。由此笔者认为，出自嫉妒心理的比较可分为两种：第一种是弱者同比自己强势者的比较，这种比较产生了弱者的嫉妒压力，这种嫉妒压力因占优的差距较大而导致痛苦；第二种是强者同比自己弱势者的比较，这种比较产生了强者的嫉妒压力，这种嫉妒压力因占优差距较小而导致痛苦。由于以上两方面，当弱者的交易替代效应小于其交易替代成本时，弱者自身关于平等、效率的替代，以及强弱者之间的交易停止。这时弱者的

（三）关于平等效率的交易是强弱参与人的讨价还价博弈

盖尔·D（2008年，第34页）指出：如果某些经济原理不能从博弈理论中推导出来，我们就只能原地踏步走，这就好比说，某些经济原理是不能从理性中推出来一样。事实上，竞争交易以至达到均衡，不仅是微观经济学而且也是博弈论研究的核心问题。并且，如果我们运用“动态匹配和讨价还价博弈”理论来分析竞争交易及其均衡，则更能揭示其内在的利益实质。这一实质正如盖尔·D（2008年，第38页）援引哈恩（1974年）所言：博弈论将均衡行为描述为一组行为人相互一致的最优行为。斯塔尔·R（2003年，第137页）则直接用博弈论概括了竞争交易均衡：每个交易者试图获得最大利益而在交易中讨价还价直至完成交易，这将导致一个大型经济的均衡；将市场经济的“核”定义为战略性讨价还价的结果。

那么，讨价还价博弈的解，或纳什讨价还价解（穆素·A，2005年，第25页）同市场竞争交易的均衡结果是否等价？盖尔·D（2008年，第68～69页等）证明了两者是等价的。他指出，将市场竞争过程看作是一个马尔可夫（MPE）过程，同时如果所有效用函数ui都是收敛的，那么这个假定能保证配置｛xt｝也是收敛的，即x∞=limxt∈P。这表明，由于MPE的重要性质是对博弈历史没有记忆，它在t时的结果只同t时的条件有关，而与t之前的条件结果无关。这样，在参与人数量很大，或参与人匿名，或博弈的时间过程有贴现等条件下，这些条件和性质就会使每个参与人等价于价格接受者，使得讨价还价过程等价于完全自由竞争市场，从而在连续、凸性、紧集（后文详论）的假定下，不能再通过交换满足ui（xi′）≥ui（xi），使得所有参与人对两种配对商品的边际替代率都是相同的，使得配对效率和帕累托效率等价（盖尔·D，2008年，第49～51页）。这样，马尔可夫（MPE）过程就会收敛于一个子博弈完美均衡（SPE），并得到市场竞争交易下的瓦尔拉斯均衡（盖尔·D，2008年，第24页、117页）。

再从讨价还价理论（穆素·A，2005年，第25页）可以推论强弱两者关于平等、效率博弈的纳什讨价还价（均衡）解，这可以简单表示为如下最大化问题的解：Max（ua-da）τ（ub-db）1-τ=Max（ua-Jb）τ（ub-Ja）1-τ。式中，ua、ub为弱者或强者在竞争交易博弈中获得的效用，da、db为衡量能否达成纳什讨价还价解的“无协议点”，它们具有成本的含义；Jb为强者产生的嫉妒压力，Ja为弱者产生的嫉妒压力。根据上述最大化问题有唯一纳什讨价还价解的条件是：ua≥da，即ua≥Jb；ub≥db，即 ub≥Ja。而上式中的 τ，1-τ则分别表示两个参与人对于在均衡时净收益的分配份额，它主要同贴现率、破裂风险等有关。

（四）关于平等、效率的竞争交易均衡

1.竞争交易均衡的产生（以埃奇沃思图解释）。图1为所借用的埃奇沃思方框图（以下简称“埃图”），以平等xi为横轴，效率xj为纵轴，强弱两个交易者分别位于右上方原点O和左下方原点O。那么在强弱两者关于平等、效率的两簇（各有多条）无差异曲线集合中，其中会有多对相应的无差异曲线相切，在切点两者各自的无差异曲线斜率的绝对值相等，而这些公共切点的连线就是帕累托最优曲线。同时这些公共切点的其中之一又是它们同预算线的切点。因而强弱两者关于平等、效率的交易在如下意义上达成了均衡：在均衡点两者各自关于平等、效率的边际替代率的绝对值相等，它们同预算线斜率（从而又是平等、效率的相对价格比）相等并使消费组合效应达到最大化。

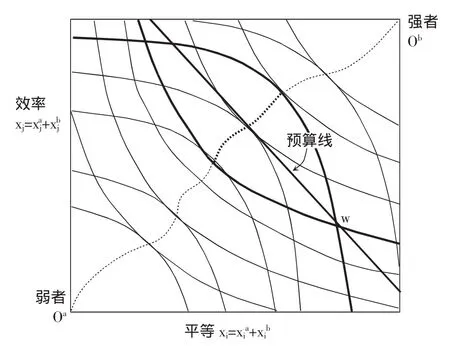
图1 强弱两者关于平等、效率竞争交易的埃图

2.竞争交易均衡的产生（以净交易图解释）。在两个消费者的纯交换经济中，应用埃图直观而方便，但不能运用于多个交易者关于两个消费品的纯交换经济，为此可将埃图转换至净交易图，同时净交易图还可以更多展示竞争交易均衡的某些重要性质（埃里克森·B，2008年，第14～17页）。为简明计，在以下净交易图中我们仍只标明强弱两个交易者，并只标上一对无差异曲线。将图1转换为图2，仍以平等xi、效率xj作为平面坐标系的横、纵轴。

通过位移△w，将原埃图的坐标系连同原点（0，0）移至初始禀赋点 W，而预算线 H（P，0）是通过此点的直线。此时，原坐标系上所有的点、向量、曲线与集合等都随同位移△w。同时，将埃图之右上半部分之强者无差异曲线逆时针翻转180°，这条曲线在位移和翻转后仍与预算线H相切；而原来埃图之左下半部分之弱者无差异曲线也随着预算线位移△w。上述过程已建构了净交易图，即图2。埃里克森·B（2008年，第19页）证明，在上述转换前后的两种方式表达的瓦尔拉斯均衡等价。

图2 强、弱两者关于平等、效率的净交易图

在图2中，在预算线的右上方，强弱两者的无差异曲线都同预算线相切，这说明强弱两者的无差异曲线在同预算线的共切点的斜率彼此相等，同时它们关于平等、效率的边际替代率在上述共切点也彼此相等，而这正是强弱两者关于平等、效率竞争交易达成的均衡。假设均衡时规范数字为1和-1，在图2中，强者之无差异曲线位于Ⅱ象限的预算线之上，切点为，这表明强者的平等少，效率多。而弱者之无差异曲线位于Ⅳ象限的预算线之上，切点为，这表明弱者的平等多，效率少。应指出在埃图中，在均衡点强弱两者的无差异曲线的公共切点同预算线的切点是三者重合的，而在净交易图中，强弱两者的无差异曲线各自同预算线的切点虽然俩俩分开，但在均衡时它们的净交易和为零。这表明它们的绝对值相等，符号相反。如上图中1）+（-1，1）=（1-1）+（-1+1）=（0，0）。推广至多个交易者的一般，其结果同上述完全一样仍为0。

在图2中，强弱两者无差异曲线都同预算线相切，还表明它们在预算约束下都已达到效用最大。此外由于预算线斜率又等于平等、效率的相对价格，即－Pi/Pj，这样当预算线H随着自身斜率而变动时，平等、效率的相对价格也随之变动。若H平坦，表明相对来说，平等的价格较高而效率的价格较低，这说明弱者的力量较大；若H陡峭，表明相对来说，平等的价格较低而效率的价格较高，这说明强者的力量较大。

3.关于平等、效率竞争交易的均衡解，是逐步排除被占优部分的最后剩余部分。

（1）图 3（再借用埃图）中，个体理性部分 IR（ε）就是由通过初始禀赋点W点的、强弱两者的两条无差异曲线Pa和Pb围成的中间镜状（阴影）区域。它表明消费分配就是在初始禀赋预算约束下，在强弱者各自偏好集重合区域之内的部分，这是排除了非个体理性分配的剩余部分之集合。

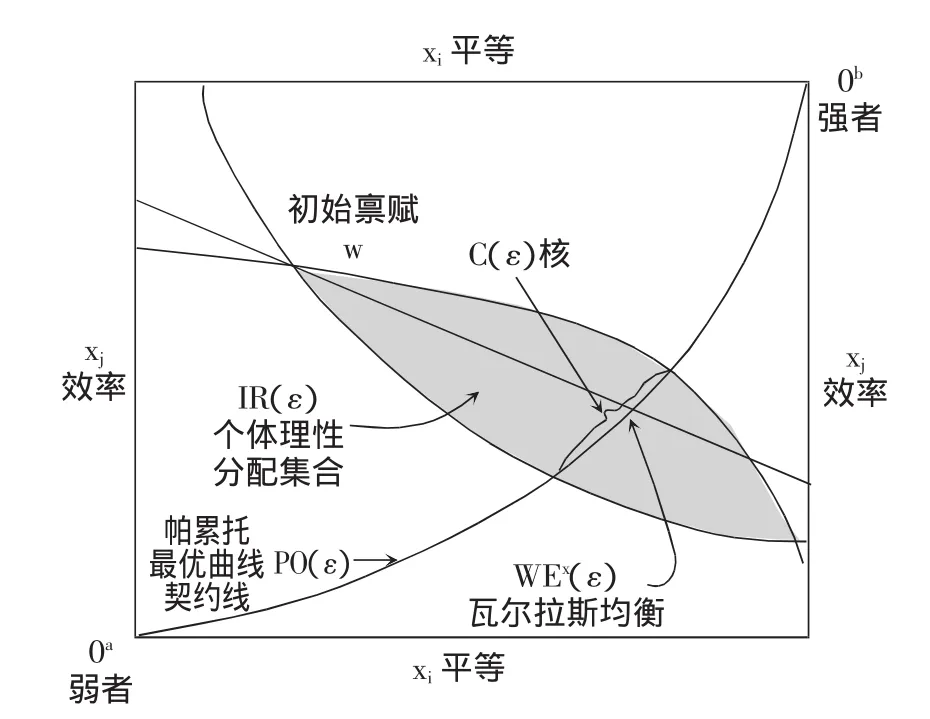
图3 个体理性、帕累托最优曲线、核与瓦尔拉斯均衡

（2）帕累托最优曲线PO（ε）和契约线，就是强、弱两者所有对应无差异曲线共切点的连线。因为这条连线上所有点对应偏好集的边际替代率在此点相等且消费者效用相对最大，这就是“不损失某一方就不能使它变得更好”的帕累托最优状况，故称为帕累托最优曲线。同时这条连线又是强弱两者关于平等效率的边际替代率相等从而达成交易的契约，故又称契约线②。总之，这是排除了非最优部分的剩余部分之集合。

（3）核C（ε），就是上述帕累托最优曲线位于强、弱两个偏好集的交集（阴影部分）之中的那一曲线段。这表明，核就是由那些在个体理性分配（在预算约束之下，两个偏好集之间）范围内但又排除了那些被占优（即不符合帕累托最优条件）的剩余部分之集合。

（4）瓦尔拉斯均衡WEx（ε）。核作为一条曲线段表明双方关于平等、效率交易仍会有多个解。但极限定理（高山晟，2009年，第176页）表明，当竞争交易者数目逐步增大时，就会排除预算约束下效用最大化集合的其他点，核就会逐步缩小。当交易者数量I→∞时，核收缩为一个点，竞争性均衡收敛为瓦尔拉斯均衡。即C（ε）→WEx（ε）∣I→∞∣。由图3可见，瓦尔拉斯均衡就是帕累托最优曲线或核（线段）同预算（或相对价格）线之交点，换言之排除了核线段同预算线交点之外的其他最优点。理论证明，这个点即这个均衡解是唯一的。总之，强弱者关于平等、效率的竞争交易发展到瓦尔拉斯均衡是逐步达到的。这一过程服从夏普利定理（埃里克森·B，2008年，第 26 页）：对任意交换经济 ε，有 WE（ε）⊂C（ε）⊂PO（ε）；并有WEx（ε）⊂C（ε）⊂IR（ε）。可见，关于平等、效率竞争交易的解，是从预算约束偏好集，到不被占优，到最优集合，直到唯一最优，这样逐步排除，直至最后剩下唯一最优解，这就是竞争交易的瓦尔拉斯均衡。

三、关于平等与效率竞争交易均衡具有存在性的条件

均衡是强弱者关于平等、效率关系的核心。经济理论认为，一切状态都是在一定约束条件下的产物。平等与效率关系的均衡，并不必然存在或不存在，它只是在一定条件下的产物。

（一）均衡存在性的概念、意义、定理和条件

上述定义表明，如果向量组是一个均衡，那么（1）均衡中消费的价值大于非均衡中消费的价值，对某商品均衡中消费的偏好，甚于任何非均衡中消费的偏好，此为实现了消费者均衡；（2）实现了生产者利润最大化，即生产者均衡；（3）供求平衡，即实现了竞争交易均衡的可行性。

另一方面从博弈论角度，这种均衡也是纳什解。纳什解的定义是“对其他一切参与人的一切策略都是最优”（姚国庆，2007年，第 39～40页），这一均衡定义同高山晟的定义是一致的。

对于我们所论的关于平等、效率的交易，运用埃里克森·B（2008年，第11～12页）的定义更为方便：交换经济的瓦尔拉斯均衡，是包含可行分配X∈F（ε，I）和价格函数P∈L′｛0｝的有序对（X，P），对所有的i∈I，xi∈фi（P），上式中фi（P）为预算集，I为商品种类，L为商品空间。这个定义表明（1）需求等于供给，即为初始禀赋。笔者认为，这其实就是预算约束问题。还有，供求平衡还可以转换为另一种说法：即超额需求为零或为非正，设超额需求为Z，有，即Z≤0。（2）每个消费者都在预算约束下最大化其效用。这是因为xi属于价格为P时的需求集，而严格偏好集Pi（xi），严格位于通过xi的无差异曲线之上的商品束集合中。

至于均衡的存在性问题，高山晟归之为均衡价格的存在性问题。他指出（2009年，第242页），均衡价格P是使D（P）=S（P）成立即供求相等的价格，是否存在这样的均衡价格P，就是均衡的存在性问题。按照前述说法，均衡价格P也是使总超额需求Z（P）=0的价格，蒋殿春（2006年，第 113页），斯塔尔·R（2003年，第114页）等也有这样的说法。因而也可以说是否存在使Z（P）=0的价格P，就是均衡的存在性问题。笔者认为，适用于本文强弱两者关于平等、效率关系的纯交换经济，那么使每个消费者的交易，在预算约束下取得效用最大化的平等效率相对价格是否存在，就是有关均衡的存在性问题。

2.均衡存在性的意义。高山晟（2009年，第213页）指出，重心在于各经济人行为之间的协调性，在相互独立的约束条件下，众多个体最大化目标同时实现，这是均衡存在性问题现代化表述的核心。何大昌（2002年，第40页）指出，根据经济主体的行为必须相互一致的均衡性定义。上述表明，在关于平等效率的纯交换经济中，在相互独立的诸条件下，在收入或禀赋预算的制约和支撑下，强弱两者对于平等与效率边际替代率的调整不但相互一致而且同时达到了消费效用的最大化，那么均衡的价格，即均衡中的平等与效率之边际替代率，存在于上述使之效用最大化的边际替代率集合之中。笔者认为，这是关于平等、效率均衡存在性的实质意义。

3.证明竞争交易均衡存在的基本原理：布劳威尔不动点定理。可以通过两个途径来证明上述均衡的存在。正如埃里克森·B（2008年，第203页）所言，如果市场需求是单值的，那说明瓦尔拉斯均衡的存在性就等价于布劳威尔定理或是KKM（卡库塔尼）定理，其中KKM定理是从另一个角度“纳什均衡是最佳反应函数的不动点”（埃里克森·B，2008年，第209页），并还要加上更为复杂的一些条件才能运用。故本文只采用布劳威尔定理方法。

布劳威尔定理指出，设S是Rn的一个非空紧凸子集，F是从S到自身的单值连续函数，则存在一个pˆ∈S 满足pˆ=F（pˆ）（高山晟，2009 年，第 212 页）。简单来说，不动点就是，无论当自变量P怎样变化，函数F（pˆ）总是等于自变量pˆ。那么，我们寻找平等、效率的竞争交易均衡是否存在，就是要寻找：若平等、效率关系是一个从S到自身的连续单值函数，则在非空、紧、凸子集条件下，存在一个pˆ，满足pˆ=F（pˆ）。以上关于平等、效率关系的F函数，其定义域和值域都是S，它是“自己到自己的映射”；有些情况这种映射要发生变化，那就是动点；有一种情况它不发生变化，它就是不动点。由于是自己到自己的映射，故可以转换成一个以1为单位，以P和F（P）为两边的正方形。某函数曲线经过该正方形45°对角线上任一点，都可以得到 F（pˆ）=pˆ。从布劳威尔不动点定理的证明过程（埃里克森·B，2008年，第175～182页；高山晟，2009年，第212～224页）可看出，不动点其实就是各参与方相互一致并实现效用最大化的那一点。

那么，从布劳威尔不动点定理如何转化等价于竞争性均衡的存在性呢？受斯塔尔·R（2003年，第116～118页）启发，就平等效率这两种消费品的竞争交易均衡而言，可作如下解释：原来强弱两者关于平等效率的对应无差异曲线都有许多交点；或者没有交点。现设有一个价格调整函数Tk（P），按超额需求Zk（P）之大小，来调节价格P，这实质是调节平等、效率两种消费品的相对价格，亦即调节它们的边际替代率，使强弱两者关于平等、效率的无差异曲线从不相交到相交，从多值（多个交点）到单值（一个切点）。这种通过竞争交易的调节，直到在预算等各种约束条件下，强弱两者关于平等、效率的边际替代率彼此正好相等，并各自达到了效用最大化；此时以相对价格P=MRSi，j（x）为弱（或强）者的边际替代率，以F（P）为强（或弱）者的边际替代率，则实现了 F（pˆ）=pˆ，表明两者的边际替代率作为不动点存在，从而达到了“相互一致并实现效用最大化”的要求，就此使得相对价格pˆ成为不动点。当然这表明关于平等、效率的竞争交易均衡存在。同时可见，这里Tk（P）是一个专为调节平等、效率边际替代率的函数。

4.满足达成布劳威尔定理——竞争交易均衡的三个主要条件。可见，既然布劳威尔不动点的存在等价于瓦尔拉斯均衡的存在，那么布劳威尔不动点存在的条件同样也等价于瓦尔拉斯均衡存在的条件，这些条件主要是：非空、紧致、凸性、单值连续函数。其中非空、单值的条件比较容易满足，就是相应的无差异曲线能够相交（有交点），但只有一个交点（属于切点）；或者说从定义域到值域的映射既有对应，又只是一一对应而非一对多点（或多点对多点）的对应。故而笔者认为，凸性、紧致性和连续性是满足上述定理和均衡的三个主要条件。进而言之，强弱者关于平等、效率关系是否满足凸性、紧致性和连续性，是布劳威尔不动点及至它们的竞争交易均衡是否存在的三个主要条件。

（二）平等与效率关系是否满足凸性条件

1.凸性的理论性质。凸组合和凸集：一般的说，给定线性空间 X 中的 xi和 xj，定义 Z=θxi+（1-θ）xj，其中0≤θ≤1，Z称为xi和xj的凸组合。或者说，如果 xi，xj∈S，且对所有的 θ，0≤θ≤1，有 θxi+（1-θ）xj∈S，那么 S为凸集（高山晟，2009年，第 13页；埃里克森·B，2008年，第43页）。上两式的文字意义是集合S内任意两点连线被集合完全包含，则S为凸集（斯塔尔·R，2003年，第 49页；阿罗·K，1988年，第53页）。而凸性的定义，则需借助几何方式，见图4：弧为函数f［θxi+（1-θ）xj］，相应的弦为函数θf（xi）+（1-θ）f（xj）。显然弦上任何一点都大于等于弧上一点，因而θf（xi）+（1-θ）f（xj）≥f［θxi+（1-θ）xj］，这样的性质称为凸性。这样弧f［θxi+（1-θ）xj］为凸函数，以其为边界包含的右上方部分，即是所有相应的弦θf（xi）+（1-θ）f（xj）都属于其的集合就是凸集（史树中，1990年，第33、41页）。上式中左式不小于右式表明弦总是不小于弧，具有重要意义。因为弦的两端必然座落在对应的弧上。故可以说，弦是弦自身中间点运动变化的轨迹，而弧是弦之两端点运动变化的轨迹。弦上任何一点θf（xi）+（1-θ）f（xj）总是大于等于弧f［θxi+（1-θ）xj］，表明弦线段中间任一点总是大于等于弦的两个端点，换言之，弦线段的中间点即两端函数之（加权平均）组合效应，大于两端各自单独效应，这就是凸性的本质。

凸性体现了边际效用和边际替代率递减的重要性质。这恰好体现了经济学的核心思想，即任何消费行为都是边际效用递减，单一消费效用总是小于组合消费效用。凸性在数理经济分析中具有极为重要的地位，“有两块基石构成经济活动的基础，其一是偏好的凸性定理”，因为“它表明消费者追求消费品的多样化或平均化，而不是把自己的消费局限在某单一物品上”（高山晟，2009年，第151页，引chipman·J语）。阿罗·K（1988年，第 53页）指出，在消费者理论中凸的无差异曲线（或偏好集合），在经济上可相应地解释为边际替代率递减性质。蒋殿春（2006年，第44页）指出，凸偏好假设其实就是边际替代率（绝对值）递减性质。盖尔·D（2008年，第48～49页）则进一步说，上述凸性和边际替代率递减性质表示行为人在最大化期望效用时是风险规避的。

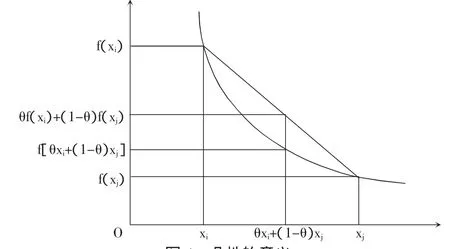
图4 凸性的意义

从图4还可以看出，凸集从而凸函数凸向原点的性质表明，如果凸函数是具有这一性质的无差异曲线，由于其边际替代率是边际递减的，那么它的趋势是从左上方向右下方倾斜的。但如果这种无差异曲线是严格凸的，则在几何图上呈现严格弯曲而不存在平坦段，这表明无差异曲线所表示的边际替代率是逐步递减的。换言之，在总消费效用不变的前提下，边际替代率只存在部分替代，而不存在完全替代。因为完全替代就是允许单一或极端消费，这在经济学理论中是不存在的。完全替代在几何图上的表现就是无差异曲线对横轴或对纵轴完全平坦（即平行），而对纵轴或横轴完全陡峭（即垂直）（斯塔尔·R，2003年，第73～74页）。

在现实中，凸性也为普遍的事实所实证。正如盖尔·D（2008年，第26页）所言，有限联盟的数量可以非常大，而且非常大的数量会产生一个凸性效应。笔者指出，这也符合统计学理论和实践：如果人数众多，绝大多数人的行为都会集中在区域中间的某一点，而呈正态分布，这表明绝大多数人都是风险规避的，厌恶极端和单一，从而偏好折中和多元。

凸性同竞争交易均衡的关系。高山晟（2009年，第93页）指出：设f（x）是定义在Rn中的凸集X上的函数，如果函数f在约束集C上，在点X达到局部最大值，并且C是凸集，那么f（x）在C上有唯一全局最大值点。其实从几何上来说，无差异曲线从两端向原点趋近的过程，就是弧弦的两端逐渐接近中间点的过程，也是逼近消费效用最大值的过程。当弦趋于0时，即刚刚变成切线时，弦的两端和中间点三者重合，这表明两端与中间的效用三者相等了，两端效用已收敛到极限点：limP（x）=C，而这正是切点（一阶导数）的数学含义。同时，这一极限点也是弦缩小到弧上，即同时属于弧上的这一点。在凸性条件下，这一点就是凸集的极值或最值，由于凸集定义，这个最值也必然包含在集合之内。总之，在一定条件下，凸集具有全局唯一的最大值点，而全局唯一最大值点正好就符合纳什讨价还价解的定义，如前所述也就符合竞争交易的瓦尔拉斯均衡定义。因此，集合具有凸性，是竞争交易均衡具有存在性的主要条件之一。

2.如果平等与效率关系满足凸性条件，那它们就成为存在竞争交易均衡的条件之一。若要考察平等效率关系是否满足凸性条件，就是要从理论上证明平等效率的加权平均组合效应θf（xi）+（1-θ）f（xj）大于等于平等、效率两个端点之单独效用，但目前对此直接证明有困难。在现实中就强者或弱者每一个消费者来说，平等和效率关系函数构成无差异曲线集合，笔者认为，如果平等效率关系具有以下表现或特点，则这些集合就是凸集，或具有凸性。

第一，平等、效率两种消费各自都呈现边际效用递减。普遍的事实证明经济学主要公理之一，即“边际效用递减”在平等、效率消费及两者的关系上仍然存在。因此在平等、效率无差异曲线上，在u（x）不变条件下，对 xi来说（对 xj也类似），由于∂xi由小逐步变大，使∂u（x）/∂xi由大逐步变小，致使 xi呈现边际效用递减，导致曲线从左上方向右下方倾斜延伸，从对xi轴陡峭（同时对xj轴平坦），到对xi轴平坦（同时对xj轴陡峭），而且中间转弯过渡的部分，则呈弯曲形状并由于“弦大于弧”而凸向原点，形成凸集。

第二，平等、效率相互的边际替代率递减。由于平等、效率的边际替代率，即，那由“边际效用递减”可直接得出边际替代率递减。另外有，则平等、效率无差异曲线的斜率为。由于dxi即xi变动额从小变大，而dxj即xj变动额从大变小，使得∣dxj/dxi∣不断减少，致使无差异曲线斜率——边际替代率不断减少，从而呈递减性质。那么这种递减的趋势如何呢？以下将其划分为三个阶段（当然这是为了便于表述，事实上它们是平滑连续的，没有理由认为它们是截然分开的）：在曲线的第一段，xi变动额dxi很小，xj变动额 dxj很大，此时∣dxj/dxi∣＞1，表明曲线斜率较大，对xi轴比较陡峭；在第二段，xi和xj的变动额差别不大，接近于∣dxj/dxi∣=1，曲线以约-45°向右转弯；在第三段，xj变动额dxj很小，而xi变动额dxi很大，故∣dxj/dxi∣＜1，表明曲线斜率较小，对xi轴比较平坦。反过来的边际替代率MRSj，i（x）之变化同上述类似，只是方向正好相反。总之由于平等、效率边际替代率的递减呈上述三个阶段的变化，故无差异曲线的斜率也呈上述三个阶段的变化，即曲线中间凸向原点的从左上方向右下方倾斜的变化，从而形成凸集。

第三，实证表明，由平等、效率两种消费品的组合效用，大于平等或效率单一消费的效用。从偏好来说，绝大多数人的实际感受是最终厌恶极端平等或极端效率的做法，而偏好两者适当的组合。“绝对平均”和“唯利是图”最终同样缺乏市场。因此从实证来说，平等、效率关系具有凸性。

综上所述，假定平等、效率关系具有上述三个表现，则这种关系具有凸性，那么平等、效率消费组合后的效用，必定大于平等或效率各自单一消费之效用。确定平等、效率适当的组合，就是确定强者或弱者关于平等、效率适当的边际替代率。那么，关于平等、效率竞争交易均衡的实质，就是在预算等各项条件约束下，强弱者关于平等、效率边际替代率通过调节相互一致并实现消费效用最大化；换言之，这种调整就是寻找强弱者各自无差异曲线斜率彼此相等，并为共切点从而是共同最大值的那一点。从理论上讲，由于平等效率的边际替代率递减，而使无差异曲线凸向原点，则凸集中的“全局唯一最大值点”在一定条件下是可以通过调节得到的。换言之，布劳威尔不动点和竞争交易均衡点存在于强弱两者关于平等、效率无差异曲线集合之中。

（三）平等与效率关系是否满足紧致性条件

紧致性的定义，由高山晟（2009年，第20，22～23，27页）援引“海湟·波莱尔定理”给出：Rn中的每一个子集都是紧的，当且仅当这个集合是闭集且有界；其中“有界”就是，Rn中的集合S称为有界，如果存在半径有限的开球包含集合S；其中“闭集”就是极限运算下封闭的集合，而任一个闭集包含它所有的极限点。斯塔尔·R（2003年，第45页）给出闭集一个简明易懂的定义：集合中任意序列点的极限点都属于集合。若 xi∈X，xi→x0，则 x0∈X，那么集合X是闭的。

应说明，紧致性就是紧集的特性。那么，紧集直接的定义就是：如果S的每一个开复盖都有一有限子复盖；或者S的每一个无限子集都有极限点，S中每个序列都有收敛子列并极限属于S（高山晟，2009年，第22～23页）。从字义可看出，紧集定义和紧致性定义的实质一样：有限序列或无限序列的极限点都包含在有界集合内。

那么，紧致性（紧集特征）是如何成为布劳威尔不动点的条件呢？这就是魏尔斯特拉斯定理：设（X，τ）为一拓扑空间，且f为X上的连续实质函数，设S为X的紧子集，那么f在S中可以取得最大值和最小值（高山晟，2009年，第24页）。由于最小值前面加个负号就成为最大值，故上述定理表明，在紧子集可以取得最优值。

假设平等、效率关系具有紧致性，那么：第一，这表明它们的集合必然是闭的，那么平等、效率无差异曲线集合，或边际替代率MRSi，j（x）集合，在它们交易的前后，其中或是有限的序列，或是无限序列的极限都在集合之内，这样根据魏尔斯特拉斯定理，集合中存在着最优值，换言之，存在着平等、效率边际替代率的最优值。第二，表明它的集合是有界的，即平等、效率之无差异曲线和边际替代率曲线的集合，在它们交易的前后，都受到预算线的约束，从而它们的替代和交易的最值以及均衡都存在于此有界的范围内。总之，假定平等、效率关系具有紧致性，它作为条件之一，可以使得布劳威尔不动点存在于平等、效率关系集合中。换言之，作为条件之一，可以使强弱两者的边际替代率相互一致并实现效用最大化。

（四）平等与效率关系是否满足连续性条件

高山晟（2009年，第20页）给出连续性的定义：称函数f在X中点x0处连续，如果对任意给定的实数ε＞0，存在一实数δ，使得对于满足距离d1（x，x0）＜δ且x∈X的x，有d2［f（x），f（x0）］＜ε；如果函数在X中所有点处都连续，那么称函数f在X上连续。埃里克森·B（2008年，第126～127页）给出更加数学化的定义：如果∀ε＞0∃δ＞0，使得，这就是在 x点连续性的 δ-ε 定义。

斯塔尔·R（2003年，第48页）指出，函数连续性概念的精髓在于：定义域内相互邻近的点映射到值域以后，映射点仍然相互接近，函数在值域中的取值没有跳跃。阿罗·K（1988年，第41页）也指出，直观上我们只是说，当自变量有微小变化时，函数也只有微小变化。笔者认为，连续性的实质含义在于，函数（映射、内生变量等）随自变量（外生变量）变化而变化，而不论这种变化微小到任何程度。将连续性同极限联系起来，可以对其含义加深理解。函数连续性定义等价于下述论断：若xq→x0，那么f（xq）→f（x0）（高山晟，2009年，第20页）。经f的映射，定义域中的一个收敛的序列，在值域中的映射是函数值的一个收敛序列（斯塔尔·R，2003年，第48页）。总之，连续性保证无限序列全面趋向极限，而不会间断、跳跃、突变和逆转。这是连续性之所以能成为满足布劳威尔不动点定理的一个条件之原因。

假设平等、效率作为消费品，以及它们关系的函数，都具有可细分性、效用可转移性以及商品守恒性质，那么平等、效率作为互为函数，其中一个微小变化必然引起另一个微小变化，其中一个收敛即趋向极限（极值、最值），必然导致另一个收敛即趋向极限（极值、最值）。这使得强弱两者关于平等、效率之边际替代变化，不会发生间断、跳跃、突变和逆转，从而使上述两者边际替代率通过变化实现一致和共同效用最大化。这样作为条件之一，有助于使上述交易产生布劳威尔不动点，从而使竞争均衡存在于上述集合之中。

四、关于平等与效率竞争交易均衡保持稳定的条件

高山晟（2009年，第242页）指出，价格P是否会收敛于原始均衡价格P，这就是“稳定性问题”。可见，所谓均衡价格的稳定性问题同存在性问题类似，就是强弱两者各自关于平等、效率的比价是否不动（存在性），是否稳定（收敛于常数）。还有，平等、效率关系的均衡也不是必然稳定或不稳定，它的稳定只是一定条件下的产物。

（一）均衡稳定性的定义、意义、定理和条件

1.均衡稳定性的定义和意义。高山晟（2009年，第251～252页，257页）给出均衡稳定性的定义：在非自治系统（有时间t）中，一个点xˆ∈X属于微分方程组x¯（t）=f［x（t），t］，式中xˆ为均衡时的消费或需求，x¯为x微分形式；如果对所有t都有f（xˆ，t）=0，则称xˆ为均衡点（状态）。在自治系统（无时间t）中，如果f（xˆ）=0，则称xˆ为均衡点。那么，当 t→∞ 时，ф（t；x0，t0）→xˆ，均衡状态xˆ称为全局稳定；或者，如果动态方程组解的时间路径从初始点P0收敛于pˆ，我们就说一个均衡（均衡价格向量pˆ）是稳定的，Samunelson称其为真正稳定的。

因此均衡稳定性的意义可作如下表述：随着t→∞，P（t）→limP（t）→C，表明随着时间趋向无限，其价格总是趋向一个极限常数。高山晟（2009年，第243～244页）以将超额需求函数写成微分方程的形式来表述：dxi（t）/dt=hi｛f［x（t）］｝。式中，hi为任何（固定）单调递增可微实值函数，f［x（t）］是超额需求函数，为需求同供给之差。该式表明，当价格移动时，超额需求的数量会发生移动，并且当价格以超额需求消失的方式移动时，市场便趋于稳定过程。总之，以价格调整市场上的稳定性被称为瓦尔拉斯稳定。

关于均衡的稳定性，就平等、效率的关系而言，笔者认为，随着时间趋向无限，强弱两者的竞争交易价格，即关于平等、效率的比价，倘若收敛于同一个常数极限，这就表明强弱两者各自对于平等、效率的边际替代率都收敛于一个彼此相等的常数极限，从而可以保持均衡的稳定性。

2.定理和条件。关于均衡稳定性的条件，有阿罗—布洛克—赫维茨定理：在瓦尔拉斯律、齐次性和总量可替代性的假设下，如下方程描述系统是全局稳定的（高山晟，2009年，第 249～251页，266～268页）。令P为均衡价格，fi（P）=fi［P（t）］为超额需求，那么这个系统是：dPi（t）/dt=fi［P1（t），P2（t），……Pn（t）］≡xi［P1（t），P2（t），……，Pn（t）］-x¯，上式中x¯（t）≡dxi（t）/dt，i=1，2，……，n。上述定理提出的全局稳定之三个条件简要表述如下（高山晟，2009年，第259页，266～268页），其中假定在以下所有关系中，t≥0，且 P（t）成立。

条件一，总量可替代性。即总量可替代率为正，有∂xi（p）/∂pj＞0，对所有的P，i≠j，i，j=1，2，……。上式也可简写为xij＞0，或αij＞0或fij（P）＞0。该式表明，对某个消费者来说，i种消费品的需求变动额对于j种消费品价格变动额的比值，即xij=∂xi/∂pj就是总量可替代率；该参数为正，表明这两种消费品具有总量可替代性。应指出，“总量可替代”同“普通净替代”不同，区别在于前者没有而后者拥有收入补偿。总量可替代条件表明，当时间t趋于无限时，交易者关于两个消费品的边际替代率（即相对比价）收敛于一个不变的常量pˆ，即均衡价格pˆ，从而保持了均衡稳定。

条件三，齐次性。可写为xi（p）=xi（αp），i=1，2，……n，对任何正数α，该式表明，一个函数同它乘上一个正的常数之后的积没什么不同。

总之，如果平等效率关系能满足总量可替代性、瓦尔拉斯律和齐次性，那么随着时间变化，即t→∞，强弱两者的竞争交易价格就会收敛于一个常数极限即稳定价格，从而实现均衡价格的稳定。

（二）平等与效率关系是否满足总量可替代性条件

1.理论性质。这从三个方面进行分析：

（1）替代品（这一部分参考了高山晟，2009年，第114-117页，但对某些数学符号做了改动）。总量可替代率为正表明两种消费品互为替代品。根据萨缪尔森交互作用关系，对所有的i和j，有总量可替代率 xij=∂xi/∂pj=∂xj/∂pi，则替代矩阵 S=［xi，j］，由上式看出S是对称的。再由欧拉定理，对所有的P，有S（P）·P=0。可见替代矩阵必有 S=0。因为 S*·P=0，故有是消费品种类。由上式可得出，在无论多少消费品中，就一对特定消费品 i，j而言，如果 x*ij＞0，则 i和 j是替代品，即满足了总量可替代条件；如果x*ij＜0，则i和j是互补品，即没有满足总量可替代条件。

理论还证明，当只有两种商品时，它们只能是替代品。因为若n=2，有这表明，此时只有当x12=x21＞0，才有可能使S=0。可见当n=2时，必有总量可替代率xij＞0，从而这两种消费品必须是替代品。而当n≥3时，由于会有xij＜0，则可能出现互补品，但其中至少有一对相互间是替代品，因为这样才能使S=0。一对消费品是替代品，表明它们具有总量可替代性，这是使均衡保持稳定的主要条件之一。

（2）总量可替代率为正，表明两种消费品的无差异曲线凸向原点。前述“若xij为正，则两种消费品只能是替代品”之结论的重要意义在于，它使两种消费品的关系呈现凸性。平新乔（2001年，第35～36页）从希克斯—斯拉茨基公式的分解中说明这一点，上述公式第1项∂xi/∂pj∣u=c为替代效应（笔者注：该项结构同总量可替代率相同，其中C为常数）。上式表明，当两种消费品之无差异曲线凸向原点时，替代效应∂xi/∂pj∣u=c为正。原因是，由于无差异曲线凸向原点，那么当pj上升时xj下降，由于xi对xj是替代的，所以在同一条无差异曲线上xi会上升，即随pj上升。反之当pj下降时，在同一条无差异曲线上xi会下降，即随pj下降。总之表明j的价格pj同i的需求xi是同向的，故替代效应∣∂xi/∂pj∣u=c为正。

笔者指出，由上述推理过程可看出，这一推理可以是逆向的：首先假设替代效应∂xi/∂pj∣u=c为正，则j的价格pj同i的需求xi必然是同向的，然后如前所述的那一变化过程必然使i，j的无差异曲线呈凸向原点的走势。这表明，只要两种消费品具有总量可替性，那它们的关系必然稳定地具有凸性，从而使两者的边际效用和边际替代率具有递减性质；又因为无差异曲线凸向原点，表明在同样不变的效用下，消费最少量的消费品，从而产生最优值。这样随着时间t→∞，在i，j的无差异曲线集合中可以找到极值和最值，从而实现均衡价格稳定。

（3）总量可替代率同边际替代率具有密切联系。我们已知：MRSi，j（x）=∣dxj/dxi∣=pi/pj，由此可得dxj/pi=dxi/pj，另一方面，总量可替代率 xij=∂xi/∂pj。从上两式可知，xij同MRSi，j具有密切的内在联系，在一定条件下，总量可替代性质可以决定和调节边际替代率从而有助于实现均衡稳定。

2.平等与效率关系如何满足总量可替代条件。在一个纯交换经济中，如果只有平等、效率两种消费品，即n=2，根据前述理论分析，平等、效率两者只能是替代品，两者具有总量可替代性，即 xij=∂xi/∂pj＞0。此外，前述理论还表明，即使在n≥3条件下，也至少有一对是替代品。这表明，在n≥3时，其中平等、效率两种消费品如果仍满足xij＞0，则平等、效率仍会是替代品，从而具有总量可替代性。可见，只要在一定条件下，平等、效率两种消费品具有总量可替代性，则就具有凸性并遵循边际替代率递减规律，因而随时间变化t→∞，强弱两者各自的边际替代率（相对价格）会收敛于一个常数极限，即收敛于一个双方一致而最优的边际替代率，从而收敛于一个稳定的均衡价格。

还应指出，既然平等、效率的交易替代是在预算约束下追求效用最大化，那么只要在分配规则重新调整的重要前提下，收入变动也会间接地影响平等效率的相对比价和关系。比如一国的经济增长了，国民收入提高了，倘若把蛋糕增长的更大一部分增加投入公共财政和转移支付政策，那么就会间接地提高平等所占比重。这里特别强调，这一“间接”提高平等之比重，必须要有收入分配比例重新调整的重要前提，即重新制定更为平均地分享蛋糕的规则。前述提高效率做大蛋糕，只是重新平均分配蛋糕的基础，如果没有重新调整分配比例即提高平等比重，那么单独提高效率绝不可能自然或必然地促进平等。这也就是在只有这两种消费品的前提下，平等与效率相互间只能是替代品而不是互补品的原因之一。反之如果是互补品，那就能够无条件地自动互补。

（三）平等与效率关系是否满足瓦尔拉斯律条件

事实上在强弱者关于平等、效率的纯交换经济中，瓦尔拉斯律条件表现为需求等于初始禀赋，而后者就是预算约束。强弱两者关于平等、效率的竞争交易，一是受到预算制约，它们关于平等、效率的替代变化，总是不会超过收入或禀赋资源；二是受到预算支撑，它们关于平等、效率的替代变化，总是能在预算约束下实现效用最大化。总之以此为可行性条件，使平等、效率的替代交易顺利进行，从而随着时间趋向无限，使这种边际替代率和交易价格收敛于一个常数极限，以实现均衡价格稳定。

此外从净交易图（图2）来看，假如收入预算增加了，从而导致预算线以及强、弱者的无差异曲线向右上方移动，这样在平等、效率比价关系和边际替代率仍然不变的条件下，使得强弱两者各自的效用仍能增加和改善。

（四）平等与效率关系是否满足齐次性条件

关于齐次性的定义，阿罗·K（1988年，第423页）指出，每个商品按相同因子上升、下降，超额需求Z不会发生变化。这表明，对每个商品的价格同时乘以某个正常数，不会改变均衡状态。斯塔尔·R（2003年，第78页）给出齐次性的意义：P的零次齐次性蕴涵只有相对价格（价格比率），对于经济中的供给和需求才是重要的，而与所报价格的数值是不相干的。这表明，在那些只需要重点关注其相对比价关系的消费品中，具有齐次性质十分重要。因为均衡是人们关注的重点，而均衡就是相对关系的均衡，所以在许多情况下，人们关注与观察的只是序数效用，即相对偏好。在现实中，在人们观察平等、效率关系时，最主要关注的是它们的相对关系以及在相对关系下达到均衡。因为在平等、效率关系中，如前所述，人性中的“嫉妒”心理有着极为重要的作用，而嫉妒是从人与人之间的相对比较而来的。

因此假设平等、效率关系满足齐次性条件，那么当强弱者的平等、效率“价格”都按同方向、同比例变动时，则平等、效率的相对比价和边际替代率都不会改变。这样，尽管一个消费者有多条平等、效率无差异曲线，若这些曲线的集合都具有齐次性，表明虽然各条曲线的效用不同，但它们关于平等、效率的边际替代率都是相同的，因此，这些曲线的斜率是相同的从而是相互平行的。当然这也表明，在无差异曲线平行移动时，平等、效率的组合效用还是可以变化和改善的，还是可以作为条件之一，在齐次性条件下向最优值调整。总之，在齐次性条件下，如果平等、效率的消费同比例增长，总量可替代性和瓦尔拉斯均衡照样不变，因而保持了平等与效率在相对关系下均衡的稳定性。

五、结论

综上所述可得出结论：运用数理经济学理论方法可以建立平等与效率关系新的逻辑框架。假设平等、效率是两种消费品，弱者、强者是两种消费者。在强弱两者关于平等、效率的纯交换经济中，在完全自由竞争的前提下，两者经过竞争交易和讨价还价博弈，有可能实现均衡。这种均衡只是在一定条件下的产物，其具有存在性的三个主要条件是，相应的平等与效率关系满足凸性、紧致性和连续性；其具有稳定性的三个主要条件是，上述关系满足总量可替代性、瓦尔拉斯律和齐次性。

注释：

①上述交易都是从强弱两者的平等、效率各自从0.5份额的初始禀赋发展到大于或小于0.5。当然也可从另一个方向比如强弱两者从各自的平等、效率为｛1，0｝或｛0，1｝的初始禀赋，通过交易替代发展到大于或小于0.5。由于相同的机理，两个方向的结果必然是一致的。

②有的文献将契约线等同于核，总之对契约线有等同于帕累托最优曲线或核的两种说法。

［1］【美】阿罗·K，英特里盖特·M.数理经济学手册（第 1卷中译本）［M］.胡显佑，等译.北京：中国人民大学出版社，1988.

［2］【美】奥肯·A.平等与效率：重大的抉择（中译本）［M］.王奔洲，等译.北京：华夏出版社，1999.

［3］【美】埃里克森·B.竞争均衡——理论和应用（中译本）［M］.费方域，孙娟，译.上海：上海财经大学出版社，2008.

［4］【美】盖尔·D.一般均衡的策略基础——动态匹配与讨价还价博弈（中译本新1版）［M］.韦森，等译.上海：格致出版社、上海三联书店、上海人民出版社，2008.

［5］【美】高山晟.数理经济学（第2版中译本）［M］.杨斌，等译.北京：中国人民大学出版社，2009.

［6］何大昌.公平与效率均衡及路径分析［D］.南京：南京师范大学博士论文，2002.

［7］何晓星，浦亦稚.平等与效率关系的实质是强、弱利益集团的博弈——兼论快乐与嫉妒变量在这一博弈中的作用［J］.经济体制改革，2007，（3）.

［8］蒋殿春.高级微观经济学［M］.北京：北京大学出版社，2006.

［9］【美】穆素·A.讨价还价理论及其应用（中译本）［M］.管毅平，郑丹秋，等译.上海：上海财经大学出版社，2005.

［10］平新乔.微观经济学十八讲［M］.北京：北京大学出版社，2001.

［11］史树中.凸性的分析［M］.上海：上海科学技术出版社，1990.

［12］【美】斯塔尔·R.一般均衡理论（中译本）［M］.鲁昌，许永国，译.上海：上海财经大学出版社，2003.

［13］【英】休谟·D.论人性（中译本）［M］.张晖，译.北京：北京出版社，2007.

［14］姚国庆.博弈论［M］.北京：高等教育出版社，2007.

Mathematical Economic Logic of the Relationship Between Equality and Efficiency

He Xiaoxing

A new logical framework on the relationship between equality and efficiency can be established by the way of mathematical economic theories.Assuming that equality and efficiency are two sorts of consumer goods,while the weak and the strong are two groups of consumers,in the pure economic process of exchange for equality and efficiency between the weak and the strong,and on the premise of perfect competition,they may realize equilibrium after competitive transaction and bargaining games.Such equilibrium only exists under certain circumstances,including three major conditions：convexity,compactness and continuity in respect of the relationship between equality and efficiency.Its stability relies on three main factors：the aforesaid relationship has its aggregative fungibility,Walras'Law and homogeneity.

equality；efficiency；equilibrium；existence；stability

F064.1

A

1007-2101（2011）03-0009-13

2011-03-08

何晓星（1946-），男，上海人，上海市发展改革研究院研究员，研究方向为制度经济学。

武玲玲

责任校对：秦学诗