粘塑性海冰流变模型的稳定性分析

王光辉，谷湘潜

（中国气象科学研究院 灾害天气国家重点实验室，北京 100081）

粘塑性海冰流变模型的稳定性分析

王光辉，谷湘潜

（中国气象科学研究院 灾害天气国家重点实验室，北京 100081）

对Hibler 1977提出的具有粘塑性本构关系的海冰模型进行了修改和稳定性分析。在已有的工作中，应用这样一个粘塑性本构关系进行数值积分时大多都必须引入人工扩散项。这里我们用数值逼近技巧提出计算相邻浮冰之间相互作用力的新方法，并且证明修改后的模型无论是海冰的收敛还是发散流动都是稳定的，模式积分无需引入人工扩散项。以二维结构为例给出了详细分析。

海冰；流变模型；稳定性；椭圆屈服曲线；插值

1 前 言

海冰覆盖地球海洋的大约7%，并且在这些海洋和大气之间形成了尽管是部分但有时非常有效的屏障，阻止海－气之间的相互交换。极地水冷却到冰点形成海冰，其大小从浮在水中的小冰粒到几米厚的大冰块。虽然通常情况下海冰是结实的， 但冰层从来不会是完整的，因为海洋中的局部加热和冰的不同方向的运动，冰破裂露出水面来。冰经常变形，将均匀一大片冰块分裂成许多形状不规则的大浮冰。与海洋大气分布状态明显相反的是海冰的分布有非常大的季节和年度变化，因而对气候模拟研究增加了复杂性[1]。长期以来，人们认识到在海洋，大气和冰之间存在许多联系。一方面，无论是海洋的上层还是海冰的覆盖都将受到大气有意义的影响。另一方面，海冰的存在有大量的气候因果关系，影响大气和海洋的温度与环流形式。海冰减少吸收在海洋表面的太阳辐射量。它是一个强大的绝缘体，限制着海洋与大气之间热量、质量，动量及化学要素的交换。此外，在全球气候模式里，对海冰动力过程的理解为大气提供了临界边界条件。在海冰模拟中有两个重要的变量，即：冰盖率和冰的移速。冰盖率对海洋和大气之间的热量交换有较大的作用。冰的移速对海洋冰的质量，海温及盐度的重新分布有重要的影响。在收敛流动中，相邻的浮冰相互作用并向对方施加接触力。而在发散流场内浮冰彼此分离，接触力消失。在维持聚合流动期间，相邻浮冰间不断增加的接触力通过破裂，变形和垂直位移形成在上面漂浮，在下倾覆的山脊式粘合冰。为了确定弹性响应，应变将被不确定的追踪，呈现出丰富的理论[2]和数值问题[3]。Hibler于1977年[4]通过在合适的时空尺度上取应力和应变率的平均值，提出了一种新的粘塑性流变理论。紧随着这个工作，Hibler 1979年提出了动力热力学海冰模型[5]，在这个模型里，厚冰和薄冰被区别对待，厚冰的区域部分定义冰的聚合。这个理论作为一种经典的海冰动力学模型被广泛接受。数值算法[6]形成了大多数其它海冰动力模型的基础。虽然计算的代价高昂，但仍有越来越多的近代模型包含复杂的流变学理论[7,8]。

然而，粘塑性模型同被采用的相应椭圆屈服曲线在它的表达式里是否存在内在的不稳定性仍是一个有争议的问题。Gray和Killworth 1995年作了稳定性分析，证明模型是不稳定的，而且问题根本就是不适定的[7]。以前的研究工作表明数值模式的稳定性依赖于人工扩散项的引进，而且，模式积分的数值结果是（至少部分）人工数值扩散项的函数。在粘塑性海冰模拟过程中，动量平衡方程和连续方程构成一组基本的方程组。不同于Gray和Killworth的处理方法，我们在这里提出：用数值逼近的方法去计算相邻浮冰之间的相互作用力。 在这个模型里，由于计算相邻海冰相互作用力的应力张量不连续，采用一个连续函数序列去逼近不连续的应力张量函数。然后，通过这个序列，重新计算相邻海冰间的相互作用力。由此得到的模型是稳定的，无需为了稳定而引入人工扩散项。

文章的其余部分安排如下：第2→部分，叙述了粘塑性模型和相邻浮冰之间作用力F的基本计算方法→。第3部分，主要对二维水平情况的相互作用力F进行近似计算。第4部分，用扰动法[9−11]对修改后的海冰模型的解的稳定性进行了分析，证明了在不引进人工扩散项的情况下，模型是稳定的。最后给出本文的结论。

2 粘塑性海冰模型

以 Gray 和 Morland 1994年提出的相互作用的连续框架描述大片浮冰的质量、动量及能量平衡关系[8]为基础。用浮冰和前导水组成的水平二维混合公式对Hilbler 1979年提出的经典框架推导类似的平衡定理[5]。

2.1 海冰的密集度与厚度的连续方程

设xoy是固定在旋转地球的Cartesian 直角坐标系，并且定义一个非惯性框架。冰的密集度和厚度满足的连续方程是[7]

2.2 海冰的动量平衡方程

考虑海冰在二维平面内移动。在海冰运动平面的Cartesian 直角坐标系内，动量平衡方程是[7−8]：

对于一个拥有椭圆纵横比为e的椭圆屈服表面，由文献[7]，粘塑性模型将通过法向流规则将应变张量D和应力张量Ne联系起来，即：

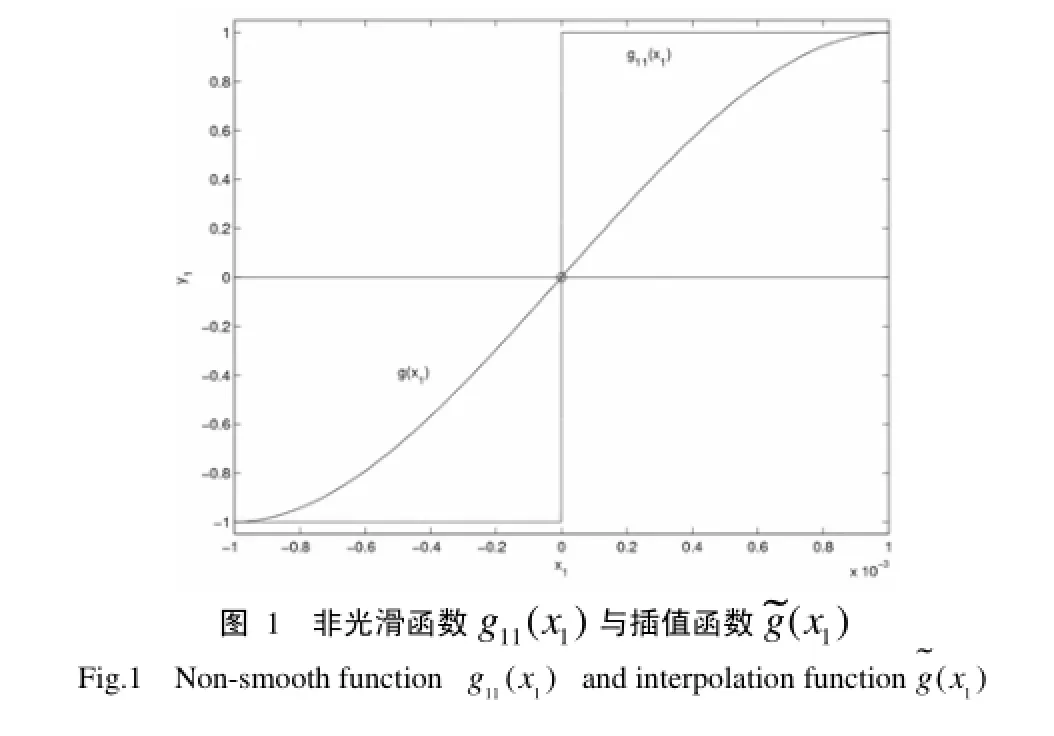
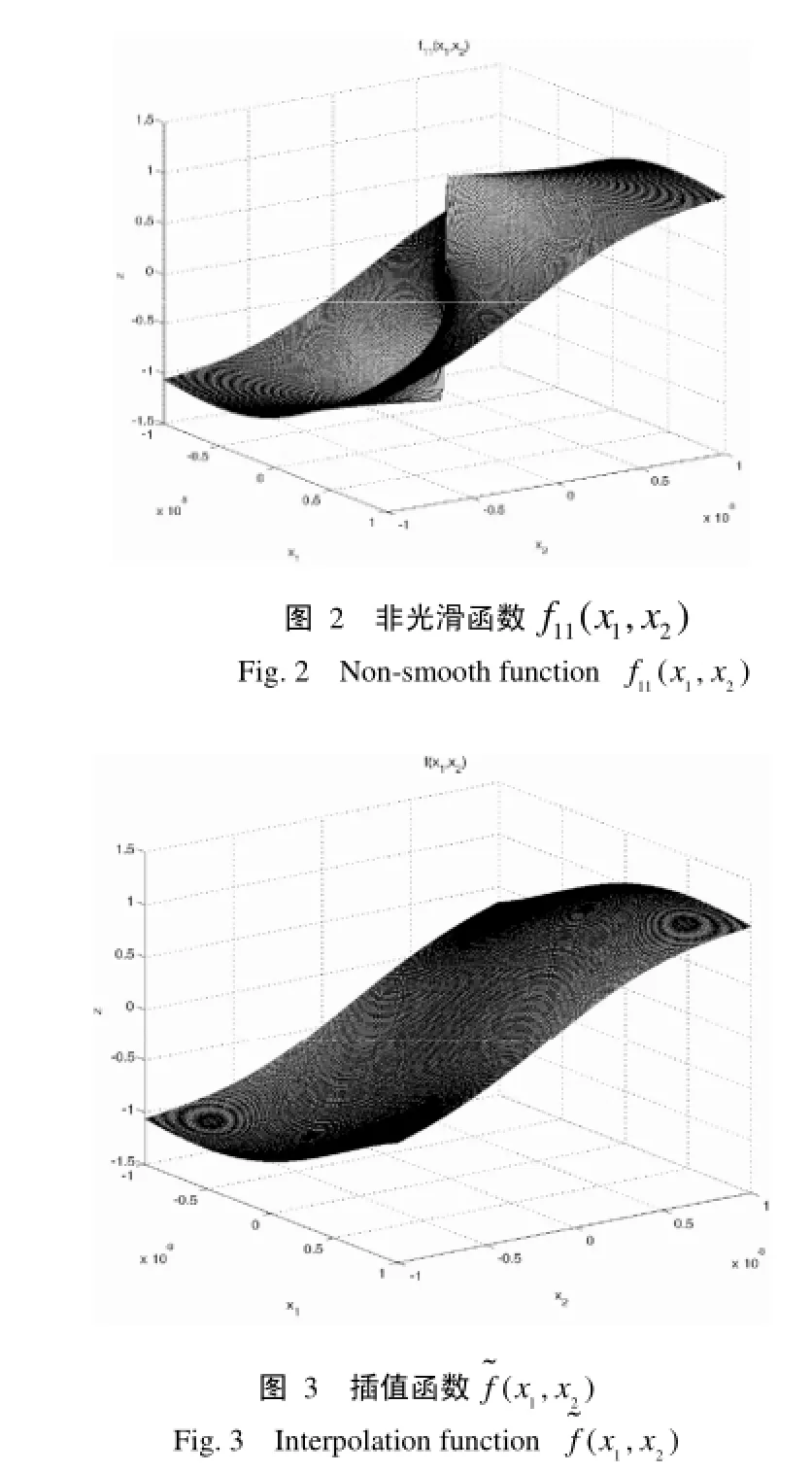
4 稳定性分析

式中上面有横杠的变量表示平衡态，上面有波浪线的量为扰动变量。将上述表达式代入(15)－(18)并舍弃高阶小量，得到其线性化方程组

5 结 论

本文通过插值逼近方法重新计算浮冰之间的相互作用力，修改了粘塑性流变模型，并用扰动理论对其解的稳定性进行了分析。证明修改后的模型在某些条件下，其解无任是浮冰收敛时的聚集还是发散时的分离，其解都是稳定的。克服了修改前模型的解存在不稳定的现象。

致谢：感谢美国Vermont 大学Yu Jun教授对本文的帮助。

[1]Washington M W, Claire L P.An introduction to Three-Dimensional Climate Modeling [M].New York: Oxford University Press, 1986.

[2]Pritchard R S.An elastic-plastic constitutive law for sea ice [J].Journal of Applied Mechanics, 1975(42): 379-384.

[3]Colony R, Pritchard R S.Integration of elastic-plastic constructive laws [J].AIDJEX- Bull, 1975(30): 55-80.

[4]Hibler W D.A viscous sea ice law as a stochastic average of plasticity [J].Journal of Geophysical Research, 1977, 82(27): 3932-3938.

[5]Hibler W D.A dynamic Thermodynamic sea ice model [J].Journal of Physical Oceanography, 1979(9): 815-845.

[6]Hibler W D.Modeling pack ice as a viscous-plastic continuum: Preliminary results.Sea Ice Processes and Models [M].R.S.Pritchard ED: University of Washington Press, 1980.

[7]Gray J M, Killworth P D.Stability of the viscous plastic sea ice Rheology [J].Journal of Physical Oceanography, 1995(25): 971-978.

[8]Gray J M, Morland L.A two-dimensional model for the dynamics of sea ice [J].Phil.Trans.Roy.Soc, 1994, 34(7): 219-290.

[9]Yu J, Kevorkian J, Haberman R.Weak Nonlinear Long Waves I in Channel Flow with internal Dissipation [J].Studies in applied mathematics, 2000(105): 143-163.

[10]Yu J, Kevorkian J.Nonlinear evolution of small disturbances into roll wave in an inclined open channel [J].Journal of Fluid Mechanics, 1992(243): 575-594.

[11]Horst L.Stability Theory: An Introduction to the Stability of Dynamic Systems and Rigid Bodies [M].Stuttgart: John Wiley & Sons Ltd.and B.G.Teubner, 1987.

Stability analysis of the viscous plastic sea ice rheology model

WANG Guang-hui, GU Xiang-qian

(State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 10081, China)

Revision and stability analysis are carried out for a sea ice model with a viscous-plastic constitutive relation of Hibler (1977) in this paper.In the existing work, numerical model integration in many studies using this viscous-plastic constitute relation are only made possible by introducing an artificial diffusion.Here, we present a new way to compute the interaction force of adjacent sea ice floes by using a mathematical approximate method.The revised model is shown to be stable in all cases including both convergent and divergent flows.The need of artificial diffusion in model integration has now been removed.As an example, we present detailed analysis for a two-dimensional configuration.

sea ice; rheology model; stability; elliptical yield curve; interpolation

P731.15

A

1001-6932(2011)06-0625-08

2011-07-07；

2011-09-26

中国自然科学基金 (40875066, 41075080 )。

王光辉(1962－), 男, 研究员, 主要从事数值天气预报研究。电子邮箱：earth54@126.com。