Voronoi生成的Clifford代数实现方法

易 琳，袁 林 旺，俞 肇 元，罗 文，闾 国 年

Voronoi生成的Clifford代数实现方法

易 琳，袁 林 旺＊，俞 肇 元，罗 文，闾 国 年

（南京师范大学虚拟地理环境教育部重点实验室，江苏 南京 210046）

引入具有维度融合、坐标无关等特性的Clifford几何代数，构建不同维度统一Voronoi生成框架及算法流程。定义了可支撑不同维度、不同对象间距离、相交及对偶关系的几何、拓扑运算，基于多重向量设计了可支撑不同维度地理对象的统一存储结构及关系表达机制，实现了基于Clifford代数的多维统一Voronoi生成算法。以中国城市气象数据为例进行了算法验证，并分析了算法复杂度。结果表明，该算法可根据输入数据维度自适应地实现相应维度的Voronoi分析，可为以维度统一为特征的GIS分析算法实现提供借鉴。

Clifford代数;维度统一;Voronoi算法

Voronoi算法是GIS最具代表性的空间分析方法之一［1－3］，Voronoi图的构建同时涉及点、线、面等多种几何对象间度量、拓扑关系的表达与计算［4］，多维Voronoi分析也得到较多关注［5－8］。但GIS中常用的Voronoi算法对二维空间数据结构依赖较强，高维扩展相对困难;而由计算几何等领域发展的高维Voronoi算法［9，10］缺乏与GIS空间数据的有效连接机制。Clifford代数以维度运算作为几何运算基础，运算具有坐标无关性，并能对不同代数系统进行有机集成［11，12］，被广泛应用于相对论物理学、计算机视觉和机器人学等领域［13－16］。谢维信等基于Clifford代数研究了二维Delaunay剖分和Voronoi图构建［17］。Dorst等给出了基于共形几何代数的多维统一Voronoi图的理论框架和理论推导［18］，并进行了二维实现;Zonnenberg实现了多维Voronoi图生成程序库CGAP［19］，受存储结构、计算引擎及不同数据类型频繁转换等制约，在算法结构、效率与运算稳定性等方面有待提高，且缺乏与GIS空间数据的有效连接。本文研究了不同维度Voronoi的Clifford代数表达及其几何特性，构建了适用于GIS的Voronoi生成算法。

1 基于Clifford代数的Voronoi算法构建

1.1 Clifford代数及Clifford代数空间

Clifford代数是一种结合代数，运算规则实现了标量运算与矢量运算、维度运算和几何运算的统一。典型的Clifford代数空间Cl（p，q）可通过式（1）定义：

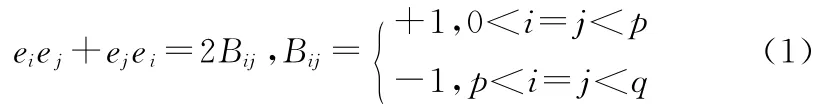
通过选取并定义不同单位向量间Clifford积的符号，可实现不同维度几何、代数空间定义，并保证不同空间中运算的坐标无关性。与复数类似，式（1）中“＋”的几何意义仅用于表达连接而非数值运算，“＋”可以连接不同维度的表达式，构成称为多重向量（MultiVector）的多维度共存的数学结构，该结构是Clifford代数中基本的数学结构之一。

在欧氏、齐次和共形这3类最常用的Clifford代数空间中，齐次空间通过增加一固定的投影维，将三维欧氏空间Cl（3，0）嵌入高维射影空间，实现了代数空间的Grassmann分级结构与几何形体分级结构的统一;而共形空间Cl（4，1）则在齐次空间基础上增加无穷远点，在保留齐次空间外积的Grassmann分级结构的同时，使得内积具备了表征距离、角度等基本度量的明确几何意义［14］。在齐次和共形空间中的新增维度仅用于辅助计算，而不影响所嵌入欧氏空间的几何特性及运算规则。Clifford代数在不同空间中的表达与相互转换，使几何计算过程具有内蕴性和直观性，在有效支撑和简化高维计算的同时，也为欧氏几何、双曲几何、射影几何、微分几何等提供统一和简洁的齐性代数框架。

1.2 基于Clifford代数的Voronoi算法设计

Voronoi的数学定义与其发生点集的维度无关，具备了发展多维统一算法的数学基础。提升法是求解高维Delaunay和Voronoi常用方法之一，通过将d维空间的点集提升至d＋1维，可将d维的Delaunay求解转化为d＋1维的凸包求解，结合Delaunay与Voronoi的对偶关系获得d维空间点集的Delaunay和 Voronoi（图1a）［20］。欧氏几何与计算几何缺乏多维统一的对象表达与空间关系计算方法，基于Clifford代数的维度运算及其坐标无关性，可实现基本几何对象维度与坐标无关的自适应表达（图1b），并可定义相应的几何与拓扑关系运算算子（图1c）［21］，从而统一并简化不同维度几何对象的表达与运算。基于Clifford代数的不同维度统一Voronoi算法流程如图1d所示。利用共形变换实现欧氏空间向共形空间转换与维度提升，基于凸包与Delaunay在维度上的对应关系，在共形空间求解d＋1维凸包后映射回欧氏空间即得Delaunay图。而Voronoi图的求解则通过将共形空间中点集的超切平面围成的包络结果反向投影回欧氏空间实现。

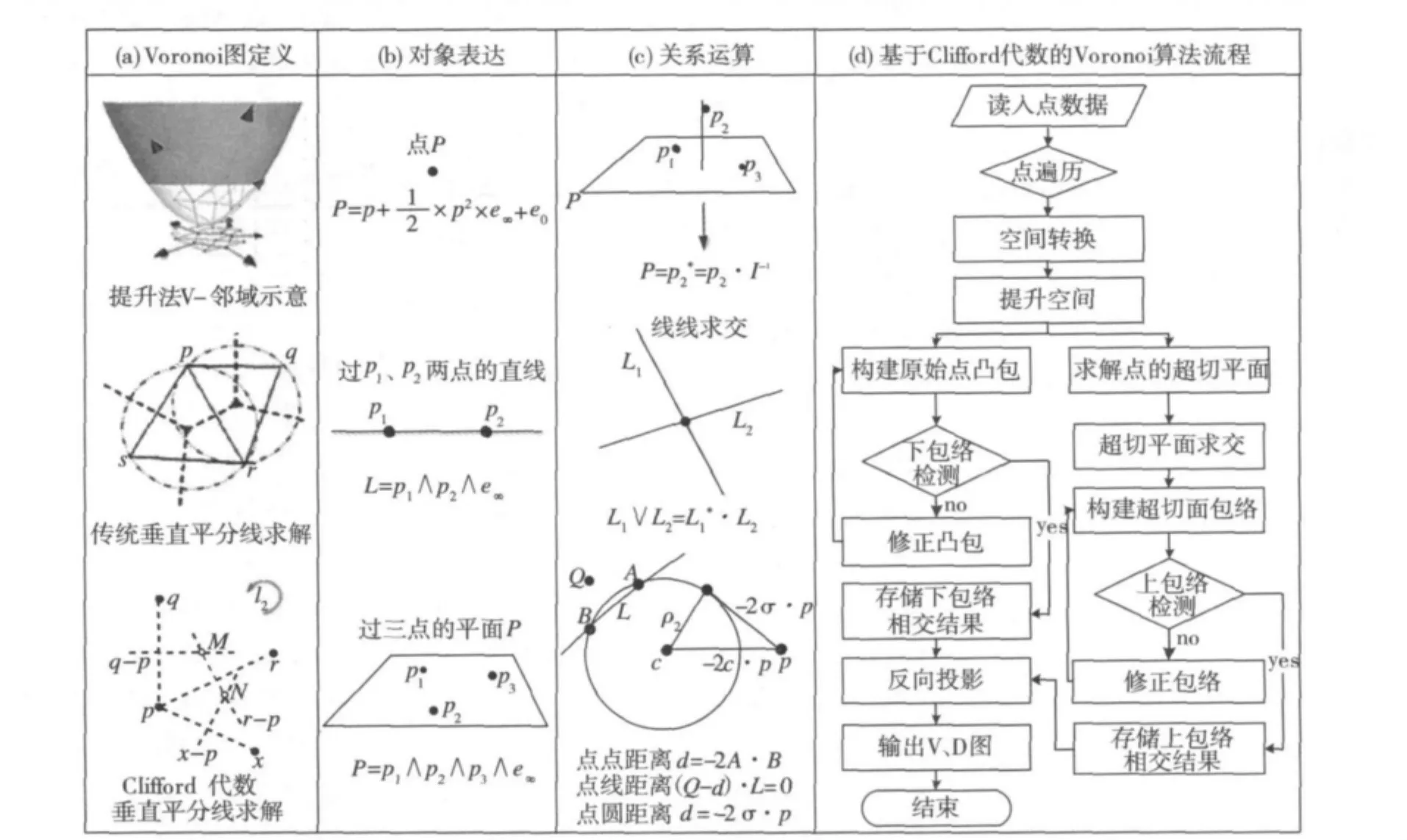
图1 Voronoi图、对象表达和基本关系运算算子定义及Voronoi-Delaunay算法流程Fig.1 The definition of Voronoi，objects expression and basic operations in Clifford space and the algorithm flow of Voronoi-Delaunay

2 算法设计与实现

2.1 存储结构与拓扑关系维护

共形空间中不同维度几何体的层次结构满足Grassmann分级结构，d维基本几何形体可直接通过d个任意共形点集的外积构建［22］，实现了维度与坐标无关的几何对象统一表达与存储。几何代数中多重向量提供了不同维度、不同类型几何对象表达、关联及数学运算结构的统一［23］。基本几何对象构建及基于多重向量的存储结构设计思路见图2。除点集外，其他几何形体存储均可通过存储所包含点的ID标识。其中线段只标定起点和终点，根据两点的外积与e∞外积构建线段方程;射线则利用点、方向、e∞外积方程表达，并采取标定起点和发射方向方式存储。该存储结构有效利用了共形空间中不同维度几何形体在构建关系和表达形式上的简洁性，不仅便于拓扑关系维护，也适用于任意维度几何对象存储。

不同维度统一Voronoi算法的关键在于拓扑关系建立，通过ID建立点与算法生成中各要素间的拓扑关系（图3）。其中，Delaunay按顺序组织每个三角形的顶点ID表达三角形间邻接关系。Voronoi中多边形（cell）可利用原始数据点 PID（N1，N2，N3）为主索引，建立其与 hyper＿segements、hyper＿rays的关联，并通过此ID连接原始数据与该点所在cell的邻接cell及各超线段、超射线。线段与射线通过SID和RID进行标定，进而实现其与所属多边形对应关系的建立。该拓扑关系结构的优势在于不仅有效组织Voronoi、Delaunay图间的连接关系，而且在CGA空间运算中确定了空间提升后地理点集数据与所求得的超切面间的拓扑关系，在对超切面相交结果进行解析时，能保持原数据与生成结果的关联关系。

2.2 核心算法实现

Delaunay和Voronoi生成的核心伪码见图4。Delaunay生成依赖共形空间中点集凸包的求解。通过以任一点作为起点，连接该点最邻近的两点依次判断每3个数据点外积构成的面与点的位置关系，确定最小边界包络。算法核心在于基于对偶算子进行点的超切面求解，以及不同维度几何对象的求交。利用对偶算子Dual（）求得输入各点的超切面，并将其存储至hyper Tangent Plane中，调用intersection（）函数计算超切面不同维度组成部分的相交结果，进而将超切面连接形成半闭合超多面体。由于外积运算具有反对称性，所构建各面具有不同的方向性，因此需要进行包络检测与修正。基于Check＿upper＿envelop（）方法对存储结果进行包络检测，若为上包络，则调用unlift＿space（）函数将包络相交边界反向投影，得到Voronoi图各边;若经检测非上包络则返回至超切平面求解，进而对包络构建过程进行修正，直至检测为上包络。迭代所有顶点输出Voronoi。

3 实例验证与算法分析

3.1 不同维度的Voronoi的生成实验与对比

本文选取2005年中国城市气象观测数据的经度、纬度、高程作为3个空间维度的试验数据（图5a），数据来源于中国气象科学数据共享服务网（http：//cdc.cma.gov.cn），共计179个站点。算法实现基于VC⧺9.0，并以插件形式集成于CAUSTA系统中［23］。二维和三维Voronoi图见图5b、图5d。结果显示本文构建算法可实现不同维度Voronoi的求解。图5c为ArcGIS二维Voronoi分析结果，两者的微小差距出现在无穷远点的射线上，谢维信等已论证了基于Clifford代数的Voronoi算法不受边界限制［17］，其结果具有更好的准确性与有效性。不同浮点精度误差的模拟实验也显示本文算法具有较强的稳健性。

3.2 算法复杂度分析

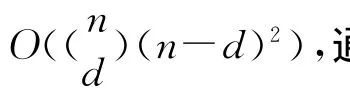
图5 多维Voronoi算法的实现及对比Fig.5 Implementation of 2D and 3D Voronoi algorithm and the results comparison

4 结论与讨论

本文利用Clifford代数在多维融合、计算的坐标无关等优势，构建了面向GIS的多维统一Voronoi算法：修改了传统提升法的Voronoi生成框架，构建了不同维度统一Voronoi算法流程;基于相应的几何、拓扑算子，实现了不同维度、不同对象间距离、相交及对偶关系运算;利用共形空间中几何对象的Grassmann分级结构，基于多重向量给出了可支撑不同维度地理对象的统一存储结构及关系表达机制;设计了用于Voronoi求解的核心算法类并进行算法实现，进而基于全国城市气象观测数据进行了二维和三维Voronoi分析。

多维GIS空间分析是GIS发展的重要方向之一。由于维度扩展所导致的复杂性及多维运算的不统一性，要求GIS分析从理论基础上能够进行多维融合，并能够支持多维统一表达与运算。本文研究表明基于Clifford代数构建的不同维度统一Voronoi算法，在算法设计上实现了多维度统一，在计算结构上实现了与Clifford代数结构的有效衔接，在计算流程上也表现出简洁直观性与几何意义明确性等特征。Clifford代数可为多维融合GIS空间分析算法构建提供全新的理论基础与数学工具。

［1］颜辉武，祝国瑞，徐智勇.基于动态Voronoi图的距离倒数加权法的改进研究［J］.武汉大学学报（信息科学版），2004，29（11）：1017－1020.

［2］李佳田，陈军，赵仁亮，等.基于线性四叉树结构的Voronoi图反向膨胀生成方法［J］.测绘学报，2008，37（2）：236－242.

［3］陈军，李志林，蒋捷，等.多维动态GIS空间数据模型与方法的研究［J］.武汉大学学报（信息科学版），2004，29（10）：858－862.

［4］KIM D S，KIM D U，SUGIHARA K.Voronoi diagram of a circle set from Voronoi diagram of a point set：Topology［J］.Computer Aided Geometric Design，2001，18（6）：541－562.

［5］LEE I，GAHEGAN M.Interactive analysis using Voronoi diagrams：Algorithms to support dynamic update from a generic triangle-based data structure［J］.Transections in GIS，2002，6（2）：89－114.

［6］KIM D，KIM D S.Region-expansion for the Voronoi diagram of 3D spheres［J］.Computer-Aided Design，2006，38：417－430.

［7］FORT M，SELLARES J A.Computing generalized higher-order Voronoi diagrams on triangulated surfaces［J］.Applied Mathematics and Computation，2009，215：235－250.

［8］BERCHTOLD S，ERTL B，DANIEL A K.Fast nearest neighbor search in high-dimensional space［A］.Proceedings of 14th International Conference on Data Engineering（ICDE′98）［C］.Orlando，Florida，1998.23－27.

［9］NILFOROUSHAN Z，MOHADESB A，REZALLI M M，et al.3D hyperbolic Voronoi diagrams［J］.Computer-Aided Design，2010，42：759－767.

［10］DOLBILIN N P.Properties of faces of parallelohedra［J］.Proceedings of the Steklov Institute of Mathematics，2009，266（1）：105－119.

［11］CLIFFORD W K.Applications of Grassmann′s extensive algebra［J］.American Journal of Math，1878，1：350－358.

［12］LI H B，HESTENES D，ROCKWOOD A.Generalized Homogeneous Coordinates for Computational Geometry［M］.Berlin Heidelberg New York：Springer-Verlag，2001.27－59.

［13］HESTENES D，SOBCZYK G.Clifford Algebra to Geometric Calculus：A Unified Language for Mathematics and Physics［M］.Reidel Publishing Company，1984.

［14］李洪波.共形几何代数与几何不变量的代数运算［J］.计算机辅助设计与图形学学报，2006，18（7）：902－911.

［15］HESTENES D.New Foundations for Classical Mechanics［M］.Kluwer Academic Publishers，1999.

［16］PERWASS C.Geometric Algebra with Applications in Engineering［M］.Heidelberg：Springer-Verlag，2009.

［17］XIE W X，CAO W M，MENG S.Coverage analysis for sensor networks based on Clifford algebra［J］.Science in China（Series F：Information Sciences），2008，51（5）：460－475.

［18］DORST L，FONGJINE L，MANN D.Geometric Algebra for Computer Science：An Object-Oriented Approach to Geometry［M］.San Fransisco：Morgan Kaufmann，Elsevier Science Ltd，2007.

［19］ZONNENBERG C.Conformal Geometric Algebra Package［D］.U-trecht University，2007，INF/SCR－2006－066.

［20］EDELSBRUNNER H，SEIDEL R.Voronoi diagrams and arrangements［J］.Discrete and Computational Geometry，1986，1（1）：25－44.

［21］YUAN L W，YU Z Y，LUO W，et al.A 3D GIS spatial data model based on conformal geometric algebra［J］.Science China：Earth Sciences，2011，54（1）：101－112.

［22］李洪波.共形几何代数与运动和形状的刻画［J］.计算机辅助设计和图形学学报，2006，18（7）：895－901.

［23］YUAN L W，YU Z Y，CHEN S F，et al.CAUSTA：Clifford algebra-based unified spatio-temporal analysis［J］.Transactions in GIS，2010，14（s1）：59－83.

［24］BRADFORD C B，DVID P D，HANNU H.The Quickhull algorithm for convex hulls［J］.ACM Transaction on Mathematical Software，1996，22（4）：469－483.

Clifford Algebra-Based Voronoi Algorithm

YI Lin，YUAN Lin－wang，YU Zhao－yuan，LUO Wen，LV Guo－nian
（KeyLaboratoryofVGE，MinistryofEducation，NanjingNormalUniversity，Nanjing210046，China）

Based on the superiority of Clifford algebra in multi-dimensional diffusion and coordinate freeing，the unified multi-dimensional generation framework and the algorithm flow of Voronoi have been constructed.Geometric operations and topological operations are defined，which can calculate the distance，intersection and dual among different dimensions and different types of geometric objects.And the unified storage structure and expression mechanism for different dimensional objects are designed with multivector.Finally，2D ＆3D experiments and comparison analysis of complexity and accuracy are given to validate the algorithm.The work proves that the designed algorithm is effective and feasible to multi-dimensional Voronoi analysis，and geometric algebra provides a new math tool to establish multi-dimensional unified spatial analysis algorithms.

Clifford algebra;multi-dimensional unified;Voronoi algorithm

P208

A

1672－0504（2011）05－0037－05

2011－05- 04;

2011－06－29

国家自然科学基金“基于共形几何代数的三维空间数据模型研究”（41001224）;国家863课题“基于Clifford代数的时空统一数据模型关键技术研究”（2009AA12Z205）

易琳（1986－），女，硕士，从事GIS开发研究。＊通讯作者E－mail：yuanlinwang＠njnu.edu.cn