改进的BP神经网络在故障诊断中的应用

陈金辉，赵雷振，杨宗宵，郭 伟

（南京信息工程大学信息与控制学院，江苏南京 210044）

改进的BP神经网络在故障诊断中的应用

陈金辉，赵雷振，杨宗宵，郭 伟

（南京信息工程大学信息与控制学院，江苏南京 210044）

针对传统BP算法存在的收敛速度缓慢和易陷入局部极小值的固有缺陷，提出用具有全局搜索能力的模拟退火算法优化BP神经网络，避免陷入局部极小值，提高网络的稳定性；引入Powell算法优化模拟退火算法，加快网络的收敛速度。最后，以齿轮箱故障诊断为例进行仿真试验，结果表明改进后的BP神经网络比传统BP神经网络的训练收敛速度快、精度高。

模拟退火算法；Powell算法；BP算法；PSA-BP算法；故障诊断

人工智能故障诊断技术因不需要建立对象的精确数学模型，部分解决了故障诊断的模糊性和不确定性等经典常规方法不能解决的各类问题，因而在故障诊断中得到了越来越广泛的重视［1］。人工神经网络着眼于模拟人脑，是一个广泛连接的巨型系统，它具有I／O非线性特性、信息的分布存储、并行处理和全局集体作用，特别是其高度的自组织和自学习能力，为故障诊断问题提供了一种崭新的途径［2］。BP神经网络是目前应用最广泛的人工神经网络模型之一。但是，BP算法采用的是梯度训练法，是一种局部搜索算法，很容易陷入局部极小和收敛速度缓慢的问题。所以很多学者提出了不同的改进算法，如变学习速率BP算法、动量BP算法、LM算法、遗传算法等［3－6］，取得了一定效果。笔者将具有全局寻优的快速模拟退火算法引入到BP神经网络用于故障诊断，主要包括：首先介绍了模拟退火算法，阐述了模拟退火算法的不足，用Powell算法优化模拟退火算法，形成快速模拟退火算法，加快模拟退火的速度；然后简要说明BP算法的训练过程，将快速模拟退火算法与BP算法结合，形成新的PSA-BP算法；最后将PSA-BP算法应用到齿轮箱的故障诊断中，仿真结果表明该算法具有很好的应用价值。

1 模拟退火算法及其改进

1.1 模拟退火算法

模拟退火（SA）算法的思想最早由METROPOLIS于1953年提出［7］，1983年KIRKPATRICK等成功将其应用于组合优化问题［8］。SA算法是一种关于Mente-carlo迭代求解策略的随机寻优算法，其出发点是基于物理中固体物质的退火过程和一般组合优化问题的相似性。SA算法是在某一初始温度下，伴随温度参数的不断下降，结合概率突跳性在解空间中随机寻找目标函数的全局最优算法，在局部优解状态下能概率性地跳出并最终趋于全局最优解［9］。模拟退火算法过程可参考文献［10］。

1.2 快速模拟退火算法

利用SA算法求解复杂问题的时候，需要大量的迭代计算，因而收敛速度缓慢。Powell算法是局部优化直接算法中收敛性较好的一种，迭代次数远远小于SA算法［11］。将Powell算法与模拟退火算法组合形成快速模拟退火算法（PSA算法），可以减小迭代次数。

该算法步骤：1）从任一初始解出发，执行Powell算法快速得到一局部极小值点；2）调用SA算法进行全局搜索；3）若在指定搜索次数内找到一个比该极小值点更小的点，则初始解被替换为此次的更优解，返回1），否则该初始解为全局最优解，退出。

2 快速模拟退火算法与BP神经网络的融合

2.1 BP神经网络

BP（back propagation）网络即误差反向传播训练的神经网络，是RUMELHART等在1986年提出的。它是一种多层前馈神经网络，网络一般由三层或者三层以上的神经元组成，包括输入层、隐含层（至少包含一个隐含层）、输出层。根据Kolmogarav定理，一个三层BP网络可以逼近n维到m维的任意连续函数［12］。所以选用三层的神经网络结构，如图1所示。

BP算法的中心思想是不断调整网络权值和阈值来修正网络的输出误差，下面给出BP算法实现过程。

设输入层有n个神经元，隐含层有q个神经元，输出层有m个神经元，输入层到隐含层的权值为wij，隐含层的阈值为θj，隐含层到输出层的权值为vjk，输出层的阈值为γk，（P，T）为含有N个样本的样本集合，p为N 个样本的任意一个，激励函数选用其中i＝（1，2，…，n），j＝（1，2，…，q），k＝（1，2，…，m），P＝（p1，p2，…，pn），T＝（t1，t2，…，tn）。

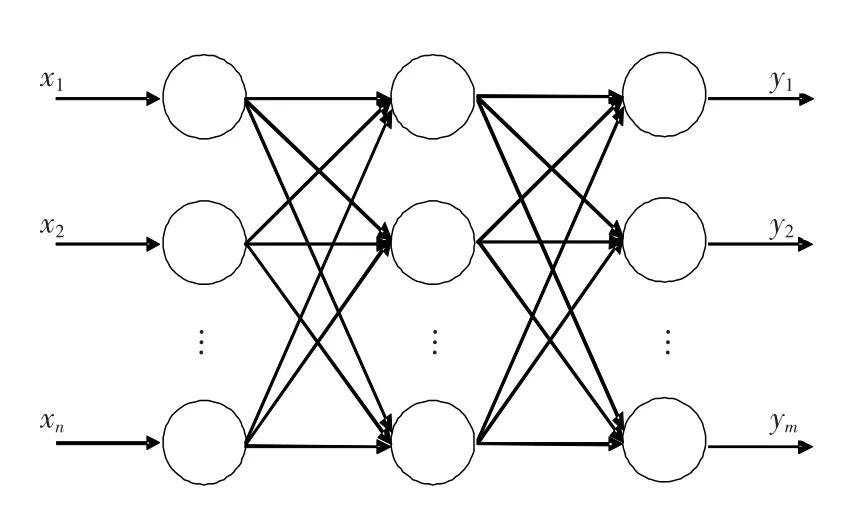
图1 三层神经网络结构Fig.1 Structure of three-layer neural network

1）正向传播过程

①初始化网络权值wij，vjk；阈值θj，γk；

②输入训练样本集（P，T）；

③计算隐含层第j个神经元输出

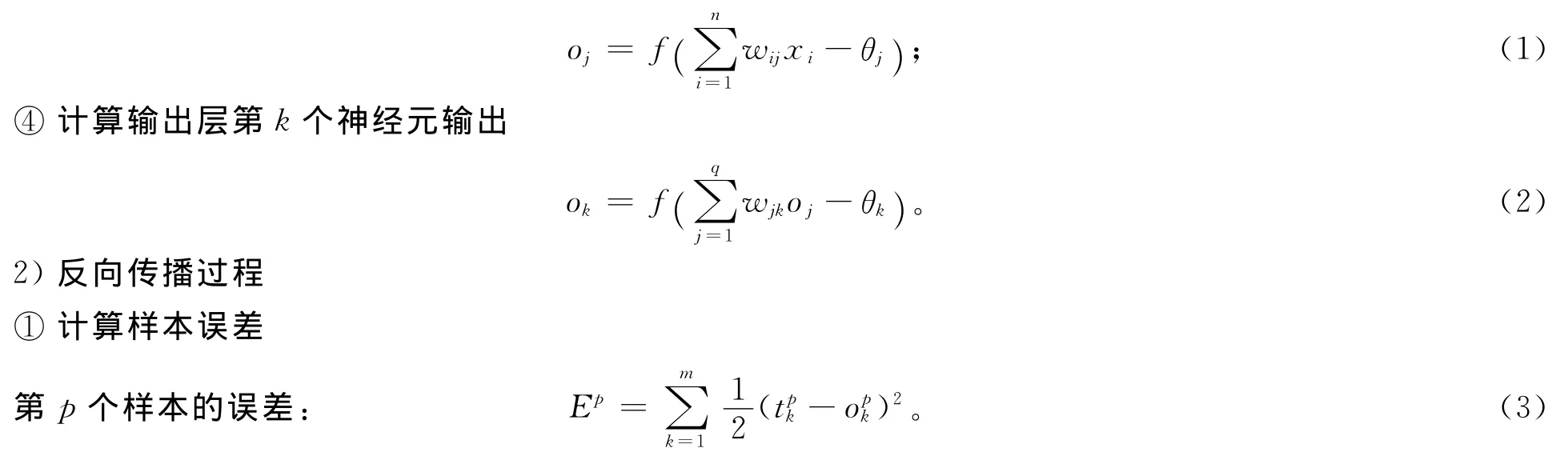
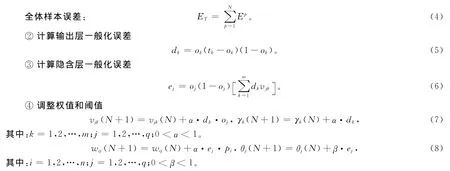
⑤返回1）③，重新计算，直至ET小于设定的值或者达到训练次数，训练结束。

2.2 快速模拟退火算法与BP算法的融合

传统BP算法是通过梯度最速下降法来修正权值、阈值向量，很容易陷入局部极小值，且收敛速度慢。为了克服BP算法的缺陷，将具有全局搜索能力的PSA算法和局部搜索的BP算法完美地结合在一起，形成PSA-BP算法，既避免了网络陷入极小值的发生，又加快了训练的收敛速度。

1）构造目标函数，即所有训练样本的平方误差的均值：

2）采用T＝T0（1＋ln（i））的降温策略。

3）初始化网络的权值W，阈值B，温度T0，迭代次数N，网络最大允许误差E＿GOAL。

4）输入训练样本。

5）计算当前的误差E，若E小于E＿GOAL，退出程序。

6）将网络的权值W，阈值B作为初始解，调用Powell算法快速搜索到某个局部极小值，得到一组新的网络权值W′、阈值B′，计算当前的误差记为E′。令W＝W′，B＝B′，E＝E′，转7）。

7）调用模拟退火算法：

① 加入随机扰动，令W＊＝W＋ΔW，B＊＝B＋ΔB，其中ΔW和ΔB 为很小的均匀分布的随机扰动。

② 重新计算误差E，记为E＊。若E＊＜E，则W＝W＊，B＝B＊；否则计算接受概率r＝exp［（－E＊－E）／（k Ti）］，Ti为当前温度，产生一个［0，1］区间的随机数p＝random（0，1），若r＞p则W＝W＊，B＝B＊，否则W＝W，B＝B。

③ 若E＊小于E＿GOAL或者超过迭代次数N，退出。否则i＝i＋1。

8）若E＊＜E，转6）；若E＊＞E，转7）。

3 仿真试验

利用新的PSA-BP算法，对齿轮箱故障进行仿真。样本集［13］选择15个特征信号作为齿轮箱故障信号，故障类型有3种，所以输入层神经元数目为15个，输出层神经元数目为3个。根据经验，试验后得出隐含层神经元数目为6个，得到15-6-3的网络结构。隐含层采用S型正切函数tansig，输出层采用S型对数函数logsig。参数设置：初始温度T＝30℃，SA最大迭代次数N＝50，系统最大误差0.001，网络总的迭代次数10 000次。归一化后的样本数据如表1所示。

图2是采用传统BP神经网络训练误差曲线图，图3是采用PSA-BP算法的神经网络训练误差曲线图，从两图的比对结果来看，传统BP神经网络经过10 000次的训练，精度远远大于给定值，收敛速度慢，训练时间长；采用PSA-BP算法的神经网络只需要经过493次的训练，精度达到并小于给定值，收敛速度快，训练时间短。同时，重复多次试验的统计结果表明，采用PSA-BP算法的神经网络更易获取全局最优解。

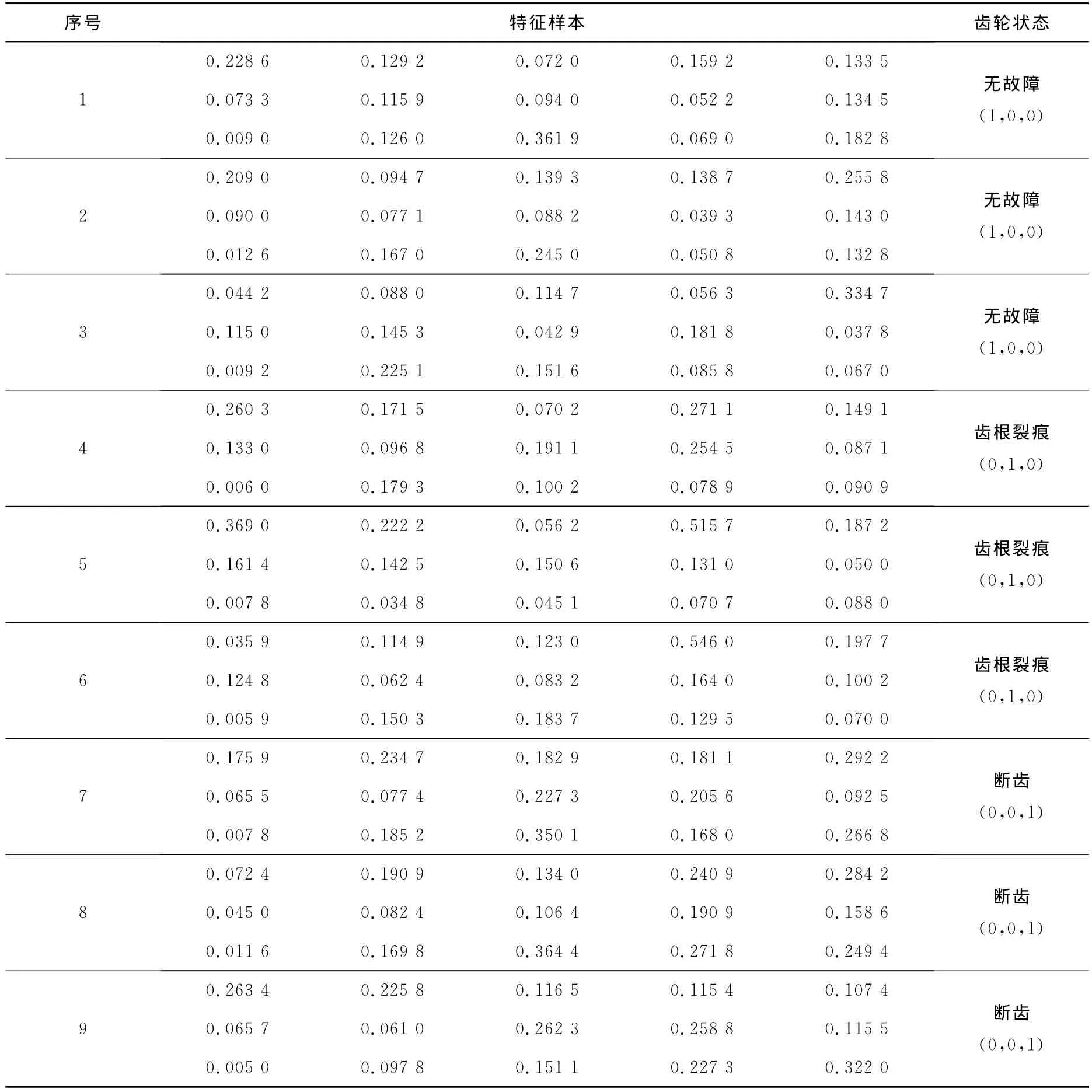
表1 齿轮箱状态训练样本数据Tab.1 Training sample data of gearbox state

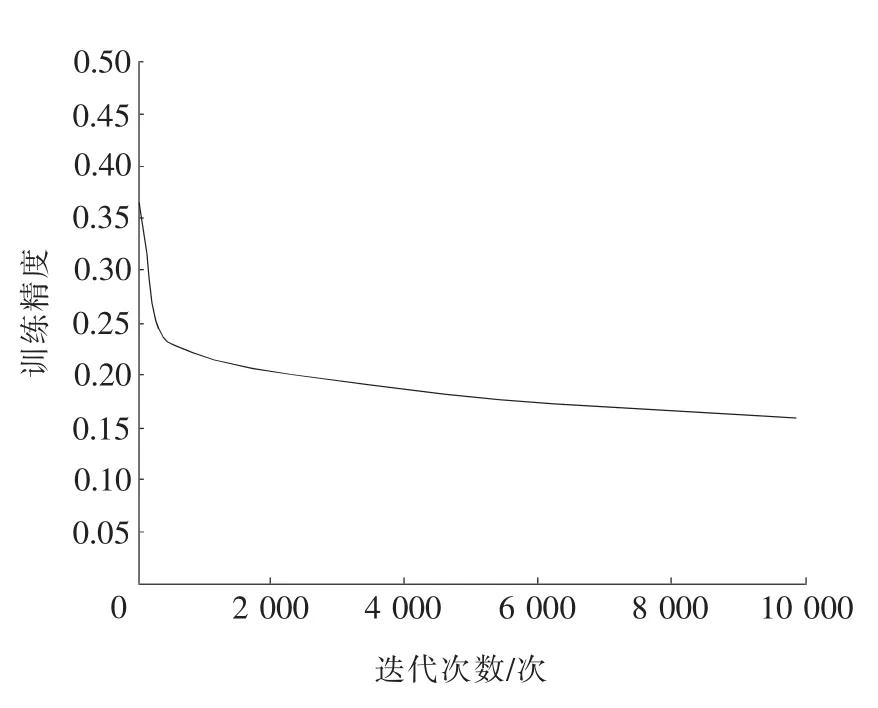
图2 传统BP神经网络训练误差曲线图Fig.2 Curve of traditional BP neural network training error

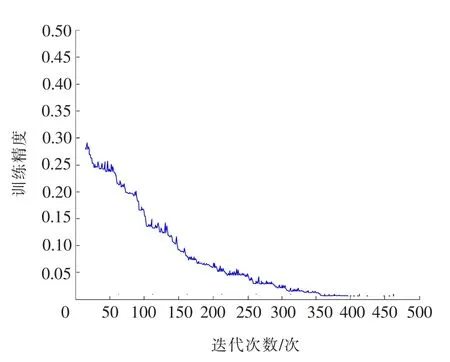
图3 PSA-BP算法的神经网络训练误差曲线图Fig.3 PSA-BP algorithm based training error curve of neural network

4 预测结果分析

为了验证PSA-BP算法的有效性，选取6组测试样本进行预测试验，归一化后的样本数据如表2所示，测试结果如表3所示。

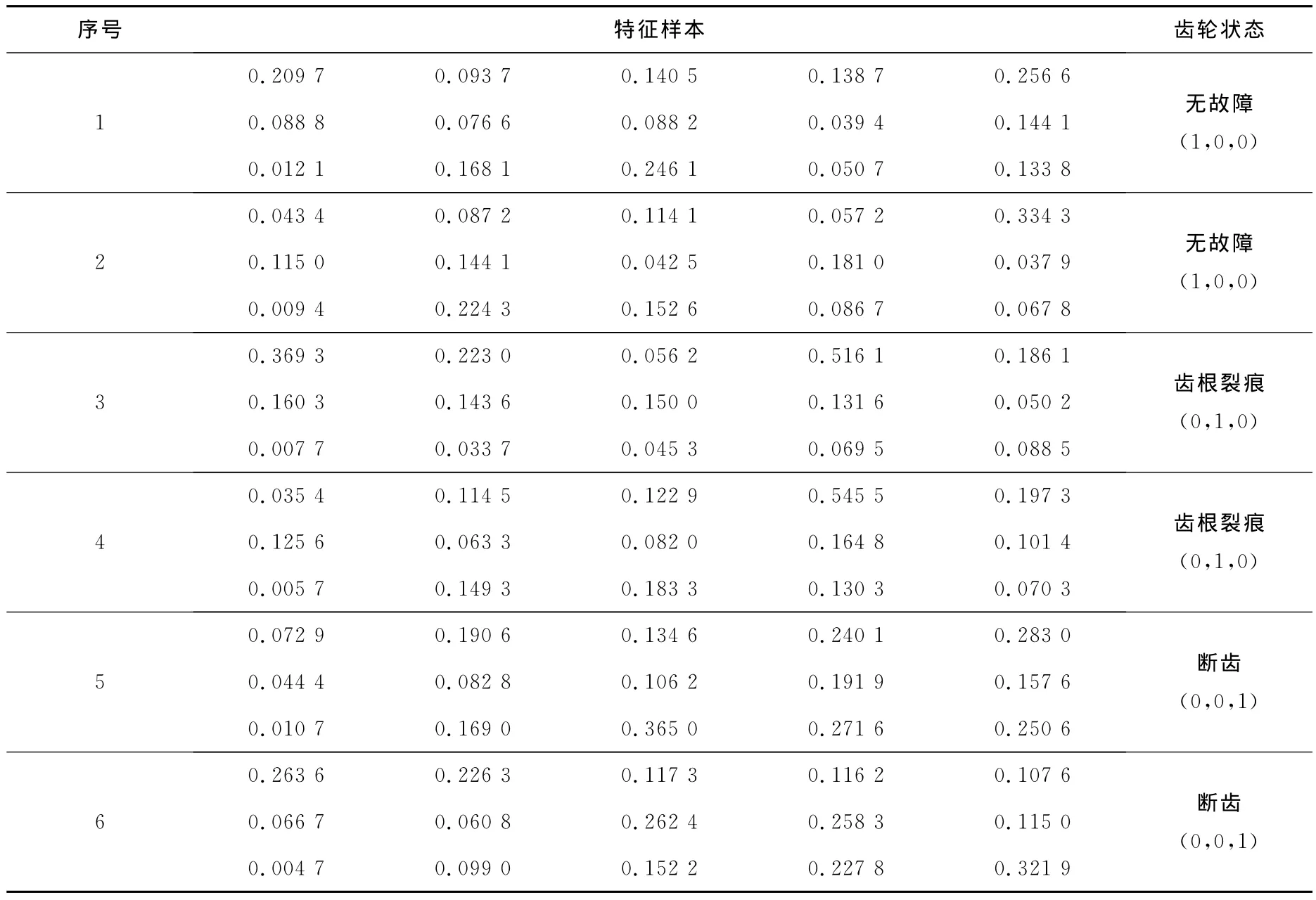
表2 齿轮箱状态测试样本数据Tab.2 Test sample data of gearbox state

从表3中可以看出，采用PSA-BP算法的神经网络诊断正确率明显高于传统的BP神经网络，特别是阈值越大，优势越明显。

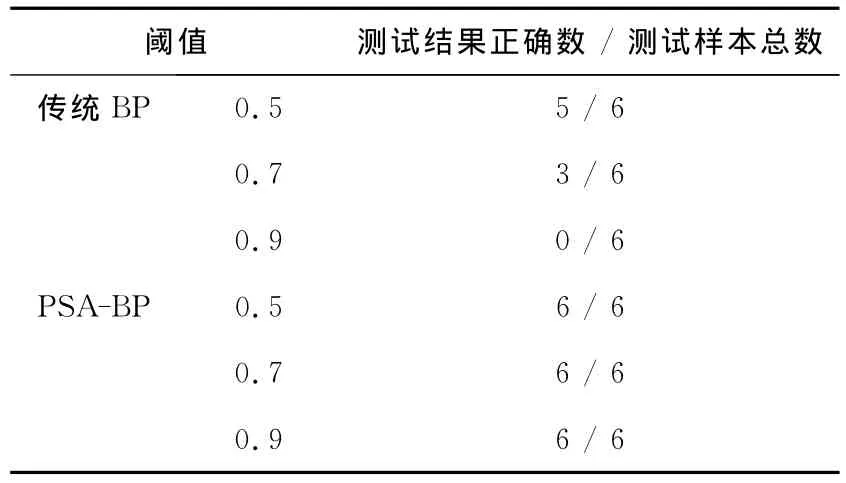
表3 PSA-BP算法与传统BP算法预测结果Tab.3 The prediction results of PSA-BP algorithm and the traditional BP algorithm

5 结 语

BP网络具有良好的非线性映射能力，故可以应用到故障诊断中。但是传统BP神经网络存在的收敛速度缓慢和易陷入局部极小值的固有缺陷，阻碍了其应用范围。为了克服BP网络的缺陷，将具有全局搜索能力的快速模拟退火算法加入到BP神经网络权值和阈值的优化中，避免了传统BP神经网络容易陷入极小值的问题，加快了网络训练速度。最后对齿轮箱故障的仿真结果表明，应用PSA-BP算法的神经网络更稳定、更可靠。

［1］ 李春华，张 生，杨智慧.基于BP神经网络电路故障诊断系统研究［J］.煤矿机械（Coal Mine Machinery），2009，30（3）：196-198.

［2］ 周世官，张 云.基于进化神经网络的模拟电路故障诊断［J］.计算机测量与控制（Computer Measurement and Control），2007，15（8）：991-993.

［3］ 周开利，康耀红.神经网络模型及其MATLAB仿真程序设计［M］.北京：清华大学出版社，2005.

［4］ 陈玉芳.BP神经网络的算法改进及应用研究［D］.成都：电子科技大学，2004.

［5］ CHIEN C Y，BIN D L.A backpropagation algorithm with adaptive learning rate and momentum coefficient［J］.Neural Networks，2002（2）：1 218-1 223.

［6］ VAN ROOIJ A J F，JAIN L C，JOHNSON R P.Neural Network Training Using Genetic Algorithm［M］.［S.l.］：World Scientific，1996.

［7］ METROPOLIS N.Equations of state calculations by fast computing machines［J］.J Chem Phys，1953，21：1 087-1 091.

［8］ KIRKPATRICK S，GELATT C D Jr，VECCHI M P.Optimization by simulated annealing［J］.Science，1983，220：671-680.

［9］ 王 凌.智能优化算法及其应用［M］.北京：清华大学出版社，2003.

［10］ 田景文，高美娟.基于改进的模拟退火人工神经网络的薄互储层参数预测［J］.信息与控制（Infornation and Control），2002，31（2）：180-184.

［11］ 肖玉刚.一种新型模拟退火神经网络及其应用［J］.控制工程（Control Engineering of China），2006，13（6）：550-552.

［12］ KOLMOGOROV A N.On the representation of continuous functions of many variables by superposition of continuous funcitons of one variable and addition［J］.Dokl Akad Nauk SSSR，1957，114（5）：953-956.

［13］ 张 捷.基于神经网络的齿轮箱智能故障诊断技术的研究［D］.苏州：江苏大学，2003.

［14］ 陈晓明，屈宝存，王小菽，等.混沌神经网络在球磨机故障诊断中的应用［J］.河北工业科技（Hebei Journal of Industrial Science and Technology），2008，25（5）：301-303.

［15］ 李森林，邓小武.基于二参数的BP神经网络算法改进与应用［J］.河北科技大学学报（Journal of Hebei University of Science and Technology），2010，31（5）：447-450.

Application of improved BP neural network in fault diagnosis

CHEN Jin-hui，ZHAO Lei-zhen，YANG Zong-xiao，GUO Wei
（School of Information and Control，Nanjing University of Information Science and Technology，Nanjing Jiangsu 210044，China）

The traditional BP algorithm has the inherent shortcomings such as low convergent speed and local minimum.So this paper proposes a simulated annealing algorithm with globalsearch property to optimize the BP neural network for avoiding the local minimum and improving its stability.In order to improve the convergent speed of neural network，the Powell algorithm is proposed to optimize the simulated annealing algorithm.Finally，the simulated results of gearbox fault diagnosis are presented to show that the improved BP neural network has higher convergent speed and precision than those of the traditional BP neural network.

simulated annealing algorithm；Powell algorithm；BP algorithm；PSA-BP algorithm；fault diagnosis

TP183

A

1008-1542（2011）05-0455-05

2011-03-06；

2011-09-01；责任编辑:陈书欣

国家自然科学基金资助项目（71071078）

陈金辉（1970-），女，新疆乌鲁木齐人，副教授，主要从事软件自动化技术、中间件技术方面的研究。