Hermite矩阵酉相似对角化的物理意义①

米斌周 杨文光

(华北科技学院基础部，北京东燕郊 101601)

Hermite矩阵酉相似对角化的物理意义①

米斌周②杨文光

(华北科技学院基础部，北京东燕郊 101601)

量子力学中的一项基本假定是代表力学量的算符是Hermite算符，由力学量算符的本征方程解出的全部本征值，就是相应力学量的可能取值。如果用测量仪器测量这个力学量的取值，只能测得其本征值。本文先从数学上严格证明了Hermite矩阵可以酉相似对角化，然后结合物理实例分析了其物理意义。

Hermite矩阵;相似对角化;物理意义

0 引言

在量子力学中，物理量是用微分算子来表示的，算子的特征值就是可测量物理量的量值。而可观测物理量的量值一定是实数。这就是说，表示物理量的微分算子一定是自伴算子。在实空间的自伴算子称为对称算子，在复空间的自伴算子称为厄米共轭算子，简称厄米算子或厄米算符。表示厄米算符的矩阵是Hermite矩阵。因此Hermite矩阵的酉相似对角化在量子物理中具有十分重要的意义。例如，解定态薛定谔方程求定态能级问题［1，2］，求解格林函数的运动方程给出自旋波的色散关系等问题都涉及到Hermite矩阵的对角化［3］。本文先从数学上严格证明了Hermite矩阵必定可以酉相似对角化，且其本征值为实数。然后结合物理实例给出详细的求解过程，分析了物理意义。

1 定理证明

引理1［4，5］(Schur定理)设A∈Cn×n，则存在酉矩阵P∈Cn×n，使得A=PΛPH，其中Λ的主对角元是A的特征值的上三角形矩阵，它们可以按照所要求的次序排列。

定理1［5］对于n阶Hermite矩阵A，存在n阶酉矩阵P，使得

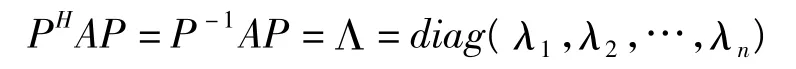
证明：对于n阶Hermite矩阵A，按照Schur定理，存在n阶酉矩阵P，使得A=PΛP－1=PΛPH。

又因A=AH，所以PΛPH=(PΛPH)H=PΛHPH

因为P为酉矩阵，故P和PH都是满秩矩阵，所以Λ=ΛH，而Λ为上三角形矩阵，那么ΛH为下三角形矩阵，二者相等，则Λ只能是对角阵，且其对角元均为实数。

根据Schur定理，A与Λ酉相似，故存在相同的特征值，又因为Λ为对角阵，其对角元即为A的特征值。

将定理1推广到实空间上，亦有：

定理2［6］对于n阶实对称矩阵A，存在n阶正交矩阵P，使得

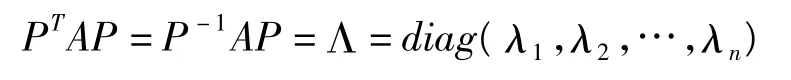
其中，λ1，λ2，…，λn是A的n个实数特征值。

2 物理意义分析

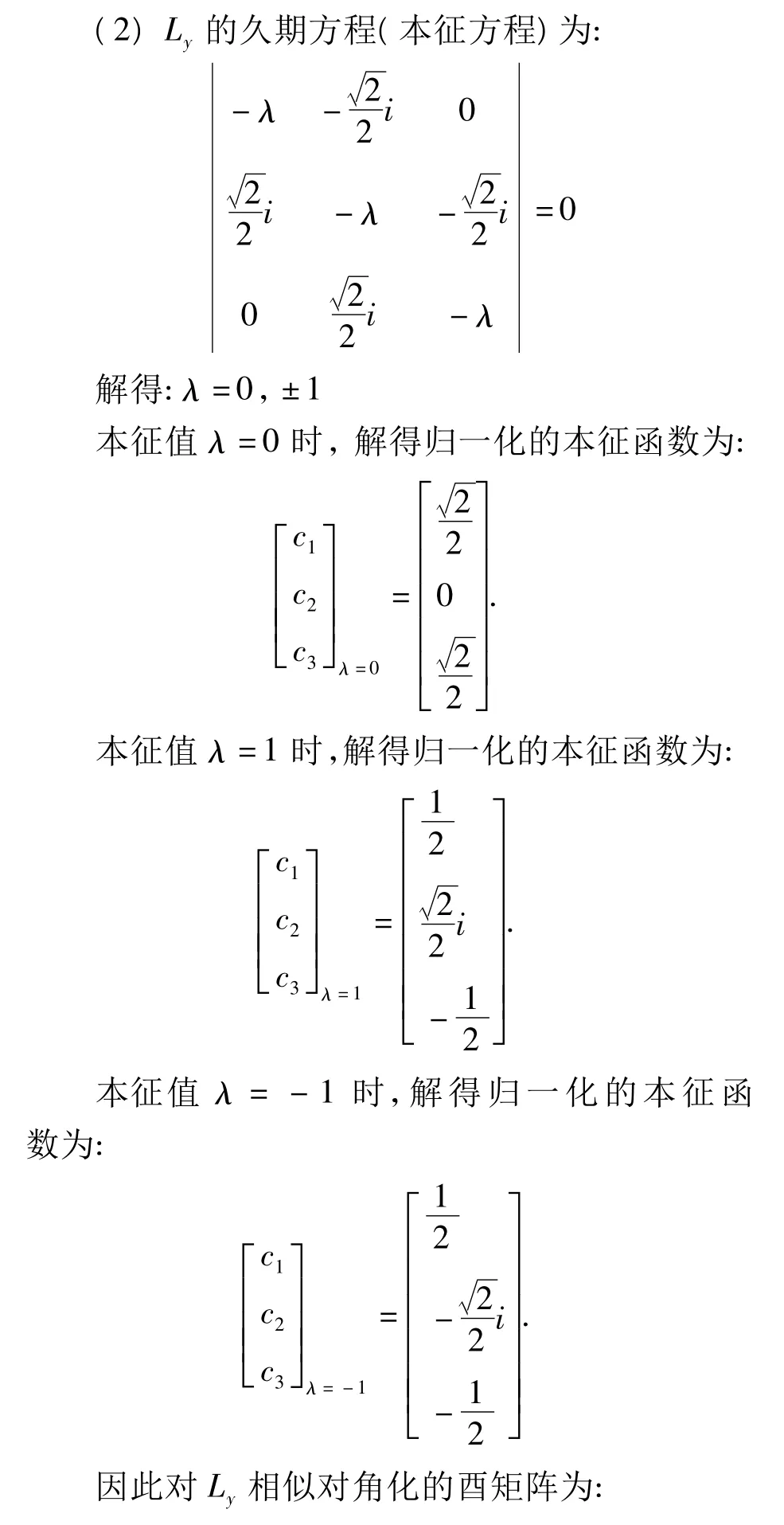
例：以|lm〉表示L2，Lz共同本征态，［L2=l(l +1)ħ2，Lz=mħ］限定l=1，取基矢为|11〉，| 10〉，|1－1〉，在这态矢量子空间建立L2－Lz表象.求Lx，Ly的矩阵(3阶)表示以及本征值和本征矢(取ħ=1).

根据基矢组|11〉，|10〉，|1－1〉的正交归一和完备性，结合上面的关系式容易求得在L2－Lz表象中，Lx，Ly的矩阵表示分别为：

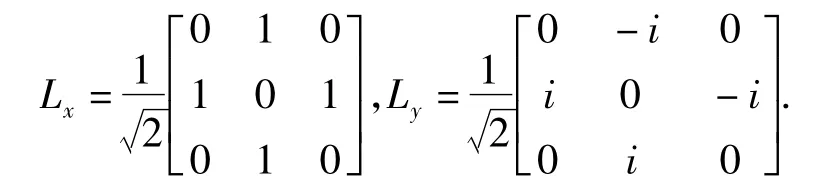
Lz在其自身表象中的矩阵表示为一对角阵，对角元上的元素0、1、－1就是它的本征值.

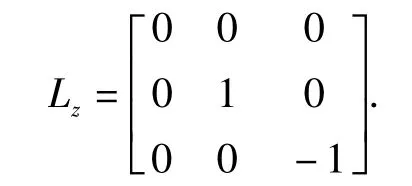
下面将Lx，Ly相似对角化。

(1)Lx的久期方程(本征方程)为：

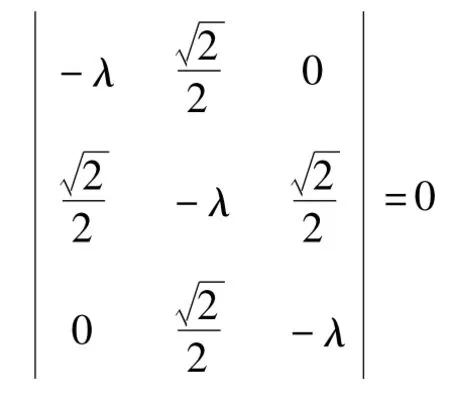
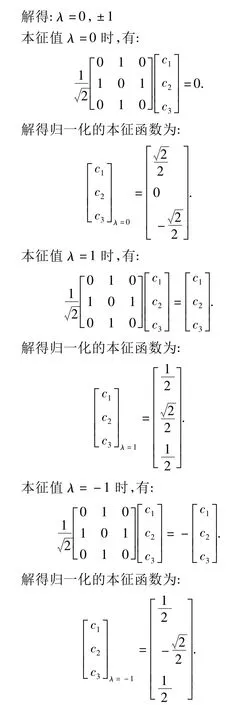
因此对Lx相似对角化的正交矩阵(物理上也叫幺正矩阵)为：

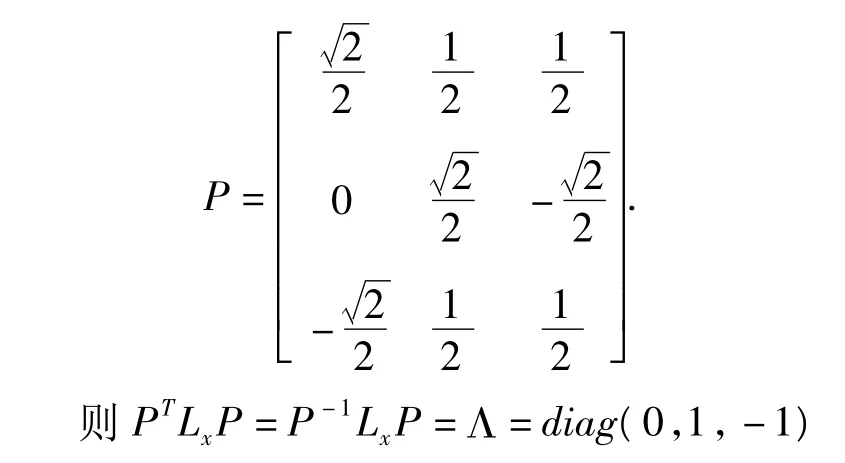
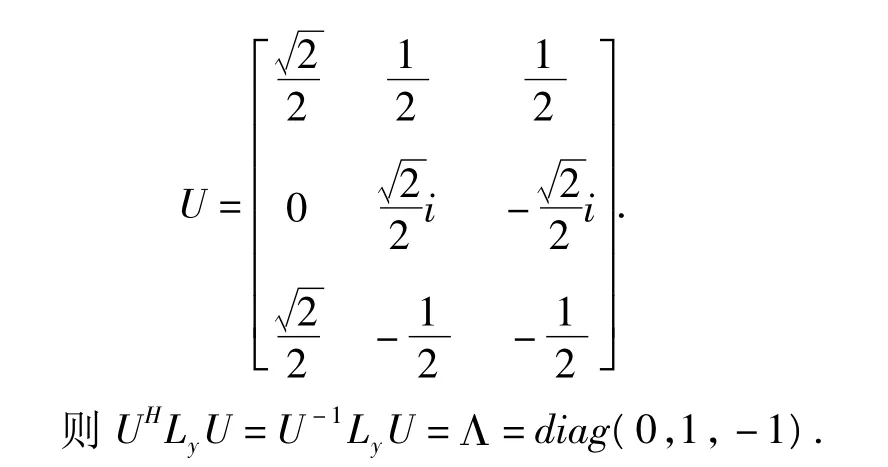
3 结语

从上面的求解过程可以看出，将Lx，Ly相似对角化的过程，就是将Lx，Ly的矩阵表示从Lz表象变化到自身表象的过程。物理上叫做表象变换，数学上叫做相似对角化，其本质是一样的。Lx，Ly都有三个不同的本征值，因此对应三个正交归一的本征矢，这和数学上的结论是一致的。如果一个热力学系统的哈密顿量H∧的本征值出现重根，也可以找到与重根个数相同的正交归一的本征矢，这种情况在物理上对应能量简并态，也就是说同一能量本征值对应几个不同的本征态。

［1］钱伯初.量子力学［M］.北京：高等教育出版社，2006

［2］周世勋.量子力学教程［M］.北京：高等教育出版社，1979

［3］王怀玉.凝聚态物理的格林函数理论［M］.北京：科学出版社，2008

［4］方保镕，周继东，李医民.矩阵论［M］.北京：清华大学出版社，2004

［5］施吉林，张宏伟，金光日.计算机科学计算［M］.北京：高等教育出版社，2005

［6］同济大学数学系.工程数学—线性代数［M］.北京：高等教育出版社，2007

Thephysical meaning of a Hermite matrix being similar to the diagonal matrix

MI Binzhou，YANG Wenguang

(Department of Basic Curriculum，North China Institute of Science and Technology，Yanjiao Beijing－East 101601)

The mechanical quantity is expressed by a Hermite operator is one of the basic hypotheses of quantum mechanics.All eigenvalues solved by the mechanical quantity operator eigenvalue equation are the possible values of the corresponding mechanical quantities.If one with a measuring instrument to measure the amount of value，eigenvalues can only be measured.In this paper，a Hermite matrix being similar to a diagonal matrix is proved in mathematics，and then combined with examples to explain its physical meaning.

Hermite matrix;Diagonalization;Physical meaning

0241.6

A

1672－7169(2011)04－0056－03

2011－07－12

米斌周(1980－)，男，甘肃庆阳人，凝聚态物理学专业硕士研究生，华北科技学院基础部物理教研室讲师。研究方向：低维物理与磁性纳米材料。