基于第一性原理计算CuxNi19-x(x＜19)混合团簇的结构研究①

冯翠菊 刘 英

(1.华北科技学院基础部，北京 东燕郊 101601;2.河北师范大学物理与信息工程学院，河北 石家庄 050800)

基于第一性原理计算CuxNi19-x(x＜19)混合团簇的结构研究①

冯翠菊1②刘 英2

(1.华北科技学院基础部，北京 东燕郊 101601;2.河北师范大学物理与信息工程学院，河北 石家庄 050800)

采用基于第一性原理计算的Chen-Möbius三维晶格反演基础上获得的原子间相互作用势参数，运用最陡下降法和共轭梯度法结合起来的最优化计算Smart方法得到了CuxNi19-x(x＜19)二元过渡金属混合团簇的稳态构型，发现Cu-Ni混合团簇中有明显Cu元素偏析现象，即Cu和Ni并没有互相混合形成有序结构，而是分别聚集在一起，所形成的体系对称性很低，呈割据状态。

晶格反演，Cu-Ni混合团簇，稳态结构

0 引言

团簇结构和性质的研究对于理解物质从微观到宏观的过渡具有重要作用，团簇结构研究的基本问题是弄清团簇如何由原子、分子一步步发展而成，以及随着这种发展，团簇的结构和性质如何变化。混合团簇可以极大的扩展单质团簇的性质，而且通过混合可以得到和加强团簇的某些特殊性质。由于组成、结构及性质的丰富多样性，混合团簇在电子、工程、催化等领域具有广泛的应用前景。

团簇在理论计算中存在着多种计算方法。最精确的从头计算方法，由于其计算量与基函数数目的五次方或六次方成正比，限制了其在电子数目较多的体系(即较大尺寸团簇中)的应用。局域密度泛函方法在小团簇计算中取得了巨大的成功，但当团簇尺寸增大到20个原子以上时，该方法同样受到了计算量的限制，对大中型团簇显得无能为力。目前对于金属团簇的研究主要是基于Gupta 、Sutton-Chen、EAM 等经验势，Gupta势已成功研究了许多团簇的结构，现在已有关于Cu、Ni、Ag、Au 等团簇［1］及 Ni-Al、Cu-Co、Cu-Au 团簇［2，3］的报道。

基于第一性原理计算的材料的结合能，运用Chen-Möbius反演［4-6］，可以严格导出的原子间相互作用对势，该方法广泛地应用于研究材料的静力学和动力学特性［7-10］。本文将Chen-Möbius晶格反演应用推广到过渡金属二元团簇的研究，运用最优化方法计算得到了CuxNi19-x(x＜19)二元过渡金属团簇的稳态结构，由此开辟了一条基于第一性原理计算的、较高效率地研究二元金属团簇的结构及其特性的途径。

1 势函数的获得与计算方法

1.1 势函数的获得

基于第一性原理计算的Chen-Möbius晶格反演获得的原子间相互作用对势，不依赖于经验的形式和方法，直接由金属和金属间化合物的第一性原理自洽能带计算和严格的晶格反演过程得出，其准确性仅仅取决于第一性原理计算的准确度和对势近似的可靠性，因此它在材料的物理性质的理论计算中得到了广泛的应用。Chen-Möbius反演的理论要点如下：

对于同种原子构成的晶体。设从第一性原理算出的晶体结合能函数可表示为：

式中x为最近邻原子间距，r0(n)为第n阶近邻的配位数，b0(n)是以最近邻距离为单位的、第n级近邻到参考原子的距离，Φ(x)为对势函数。为了理论上处理的方便，通过{b0(n)}的自乘得到{b(n)}，{b(n)}可认为构成乘法半群，这里多出的虚格点相应的虚配位数均为零。这时有

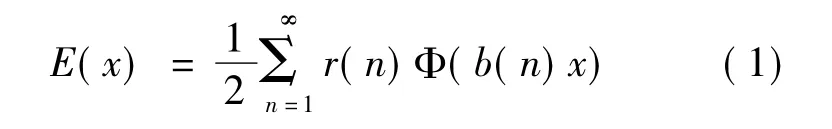
这里

由此可反演出的原子间相互作用势普遍公式

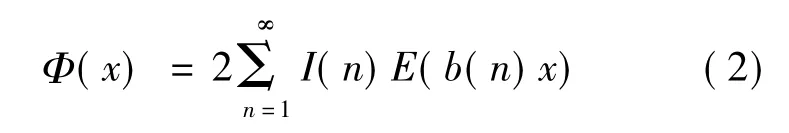
式中I(n)可通过下式求出

这里求和号下b(d)|b(n)表示对所有这样的b(d)求和：即b(d)∈{b(n)}，且可以在{b(n)}中找到一个{b(k)}，使得b(d)b(k)=b(n)。

可以证明，(2)式是(1)式的解：

关于异种原子间相互作用势问题可以通过以下的方案解决［6］，即认为通过纯元素晶体反演出的原子间相互作用势在二元合金中仍然有效，如此，可以从合金的总结合能中扣除同种原子之间相互作用对结合能的贡献而得出异种原子的“偏结合能”曲线，从偏结合能曲线反演出异种原子之间相互作用势。

表一中给出了Chen-Möbius晶格反演得到的原子间相互作用对势，然后利用Morse势形式拟合得到的参数，其中Rcut表示计算原子间相互作用对势的截止距离。

1.2 计算方法

基于原子间相互作用势，寻找团簇的稳态结构可以通过团簇的能量最小化过程实现。团簇的能量最小化过程实质上是一个多元函数的极值问题，我们采用最陡下降法(Steepest descents)和共轭梯度方法(Conjugate gradient)有机结合起来的Smart方法［11］。

由于在极值点附近能量的梯度趋于零，最陡下降法在系统趋近极值点时收敛变慢，尽管如此，这种方法由于运算稳定，仍被广泛采用或作结构能量最小化的预处理方法。共轭梯度方法以及各种Newton-Raphson方法对于偏离局域极值较大的系统构型(即势能曲面偏离二次曲面较大)是不稳定的。另外，Newton-Raphson方法需要的存储空间较大，不适于大体系计算。

随着团簇的尺度增加，团簇可能的构型数目增加非常快，显然我们不能用穷举的方法得到团簇的基态。实际计算中，判断系统最小化后的构型是局域极小还是全域极小，是一个难以回答的问题。在我们的计算中，采用不同的系统构型进行多次能量最小化，由各极值点的能量值判断能量最优化结构。对每一个固定原子数的团簇，我们随机地选取系统1000～2000个不同的初始构型进行能量最小化。本文首先采用最陡下降法对团簇的结构进行预处理，然后采用共轭梯度方法计算团簇的稳态结构，从而找到二元金属团簇的最小能量结构。当然所找到的每一固定原子数的稳态结构不止一种，每种原子数的团簇都分别对应着多种稳态结构，但其中有些是亚稳态，通过对它们的能量比较，我们可以找到(近似的)最小能量结构，也就是要找的最稳态结构

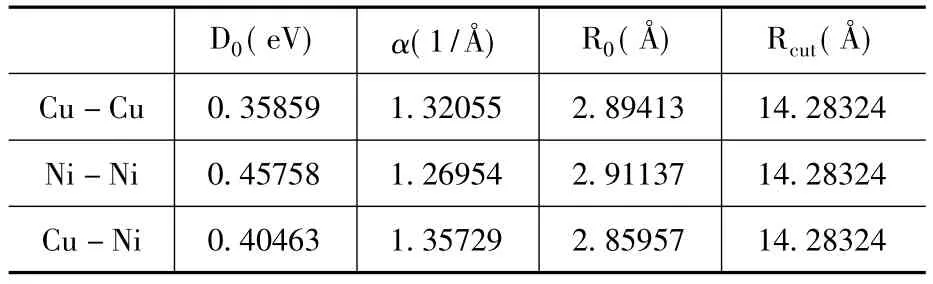
表1 Chen-Möbius晶格反演得到的原子间相互作用对势参数

2 结果与讨论

图1列出了CuxNi19-x(x＜19)各种成分的稳态构型，从中可以看到随着Cu原子数的逐渐增大，混合团簇CuxNi19-x的稳态构型都是三个五边形金字塔结构互相交叉构成的对称结构，即双二十面体套接结构，但由于Cu原子和Ni原子的半径不同而发生了轻微的形变。在CuNi18中，唯一的Cu原子占据了双二十面体的一个顶点，而不是占据中心位置，这是由于两种元素具有不同的表面能造成的，Cu的表面能比Ni的表面能低，在Cu原子和Ni原子形成混合团簇时，Cu原子会自动占据团簇的表面位置，而Ni却占据了内部位置，形成了偏析现象。同样的现象也发生在x=2、3、4，以及 x=12～18的情况下，即在Cu、Ni原子数混合比例相差较大时，有明显的Cu偏析现象。当两者的混合比例相差不大时，我们同样观察到偏析现象，Cu和Ni并没有互相混合形成有序结构，而是分别聚集在一起，所形成的体系对称性很低，呈割据状态。这种割据状态的形成，可以看成Cu、Ni合金微观不均匀性的具体体现，这导致了宏观上Cu-Ni固溶体的体现。

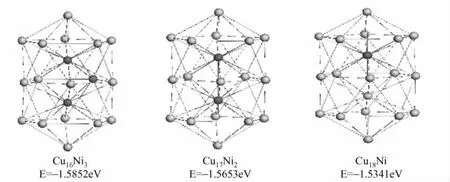
图1 CuXNi19-x的稳态构型 深色球代表Ni，浅色代表Cu

同样我们也计算了CuxNi55-x的稳态构型，图2我们给出了Cu8Ni47、Cu27Ni28的稳态构型，这些稳态构型都是二十面体结构，一个原子占据了二十面体的中心，外壳层包含了两层原子，最外面一层包含了42个原子，次外层包含了12个原子。由图可以明显看出，Cu、Ni原子混合比例相差较大时，Cu原子明显的偏析，混合比例相近时，Cu也偏析呈明显的割据状态，这一计算结果与J.M.Montejano-Carrizales等人［12］计算结果相一致，这说明了我们计算的可靠性。

图2 Cu8Ni47Cu27Ni28的稳态构型深色球代表Ni，浅色代表Cu

3 结论

本文采用基于第一性原理计算的Chen-Möbius三维晶格反演基础上获得的原子间相互作用势参数，运用最陡下降法和共轭梯度法结合起来的最优化计算Smart方法得到了Cu-Ni二元过渡金属混合团簇的稳态构型，发现CuNi混合团簇的稳态构型与纯金属Ni团簇的基态构型完全一样，只是由于Cu、Ni原子半径的不同而略有畸变;混合团簇中Cu原子趋于占据团簇的表面位置，而Ni原子趋于占据中心位置，即Cu-Ni混合团簇中有明显Cu元素偏析现象，Cu和Ni并没有互相混合形成有序结构，而是分别聚集在一起，所形成的体系对称性很低，呈割据状态。

［1］ J.Oviedo，R.E.Palmer，J.Chem.Phys.，117(2002)，9548.

［2］ J.Jellinek，E.B.Krissinel，Chem Phys，lett.258(1996)，283; ib.id， Chem， Phys.lett.272(1997)，30

［3］ J.Wang，F.Ding，el.al.，Solid State Commun，119(2001)，13.

［4］ M.Li and N.X.Chen，Phys.Rev.B52(2)(1995)997-1003.

［5］ M.Li and N.X.Chen，Z.Phys.，B100(2)(1996)169 - 172; M.Li， S.J.Liu， N.X.Chen，Y.G.Teng， W.X.Zhang， and S.Z.Zhang，Phys.Lett.，A169(5)(1992)364-370.

［6］ M.Li，S.J.Liu，and N.X.Chen，Phys.Lett.，A177(2)(1993)134-138.

［7］ N.X.Chen，Z.D.Chen，Y.N.Shen，S.J.Liu，M.Li，Phys.Lett.，A184(4-5)(1994)347-351.

［8］ M.Li and N.X.Chen，Phys.Rev.B52(2)(1995)997-1003.

［9］ M.Li and N.X.Chen，Z.Phys.，B100(2)(1996) 169 - 172; M.Li， S.J.Liu，N.X.Chen，Y.G.Teng，W.X.Zhang，and S.Z.Zhang， Phys.Lett.， A169 (5)(1992)364-370.

［10］ M.Li，S.J.Liu，and N.X.Chen，Phys.Lett.，A177(2)(1993)134-138.

［11］ J.P.Perdew，J.A.Chevary，S.H.Vosko，K.A.Jackson，M.R.Pederson，D.J.Singh，C.Fiolhais，Phys.Rev.，B46(11)(1992)6671-6687;J.P.Perdew，Physics Letters，A165(1)(1992)79-82;J.P.Perdew， Y.Wang，Phys.Rev.B45(23)(1992)13244-13249.

［12］ J.M.Montejano-CarrizalesM.P.Iniguer and.A.Alonso，Phys.Rev.B49(1995)16649-16658.

First-principles study of the stable structures of CuxNi19-x(x＜19)bimetallic clusters

FENG CuiJu

(Department of basic courses，North China institute of Science And Technology，Yanjiao Beijing-East 101601)

Using first principles total-energy calculations and the Mobius inversion method in metal Cu，Ni and Cu-Ni，We obtained the pair-potential from cohesive energy.Structural of Cu-Ni bimetallic clusters derived from the smart method are presented and discussed.In Cu-Ni clusters，the Cu atoms preferentially occupy the surface sites，whereas the Ni atoms occupy the interior of the cluster.Cu segregates to the surface in the Cu-Ni clusters.

Chen’s 3D lattice inverse method;bimetallic clusters;stable structure

O469

A

1672-7169(2011)01-0071-05

2011-01-04。基金项目：华北科技学院科研基金(B09017)。

冯翠菊(1970-)，女，河北藁城人，硕士，华北科技学院基础部讲师，研究方向：材料的模拟与设计。