学生综合素质评估的层次贝叶斯网络聚类方法

李兰春，王双成，王 辉

（1.上海立信会计学院外语学院，上海 201620；

2.上海立信会计学院数学与信息学院，上海 201620；

3.中央民族大学信息工程学院，北京 100081）

学生综合素质评估的层次贝叶斯网络聚类方法

李兰春1，王双成2，王 辉3

（1.上海立信会计学院外语学院，上海 201620；

2.上海立信会计学院数学与信息学院，上海 201620；

3.中央民族大学信息工程学院，北京 100081）

针对学生综合素质评估特点和现有评估方法存在的问题，建立了学生综合素质评估的层次朴素贝叶斯网络聚类方法，这种方法不需要许多例子，甚至在没有例子的情况下也能够进行规则提炼和预测.实验结果显示，层次朴素贝叶斯网络聚类方法具有良好的预测准确性，这将使基于层次朴素贝叶斯网络聚类的学生综合素质评估更加可靠.

学生综合素质评估；指标体系；层次朴素贝叶斯网络；聚类

0 引言

学生综合素质评估［1－2］是检验学生全面发展水平的有效方法之一，同时也为加强学生思想教育和管理工作，以及制定培养学生全面发展策略提供依据.学生综合素质评估是一个非常复杂的问题，其中有两个关键的因素：一个是建立指标体系，指标体系是评估的基础；另一个是运用数学或计算机智能方法对指标进行综合处理，经过识别和判断获得评估等级.

目前的评估方法主要采用三级指标体系［3－5］，在同级（二级或三级）指标之间相互独立的假设下，通过二级和三级指标的层次线性加权求和，以及计算结果的区间范围划分来进行等级计算.而现实中的同级指标之间一般并不相互独立，而且等级与二级和三级指标之间的关系往往也是非线性的.现有的评估方法只注重现在，而忽略过去（历史），但过去对现在往往也有很大影响.使用二级和三级指标（属性）对一级指标（类）进行等级识别和判断是一个分类（或聚类）预测问题.基于分类（或聚类）的等级预测不需要线性关系的假设，可不受完全相互独立性的约束，而且能够有效利用历史信息，因此在评价的可靠性方面具有优势，并可开拓综合评估的新思路.

分类技术是使用计算机对人类概念学习与应用能力的模拟，已成为机器学习、模式识别和数据采掘等领域研究的核心内容之一.现已发展了许多著名的分类器，如朴素（naive）贝叶斯分类器、TAN分类器、C4.5分类器、支持向量机和神经网络等，它们各有特色，已在许多领域得到了广泛的应用.但这些分类器都需要一定数量的例子用于学习（训练），当具有不完整例子（类标签很少、某些类标签残缺或根本没有类标签）时，由于分类器得不到很好的训练（甚至一些参数无法估计），将导致分类预测结果不可靠，甚至无法进行分类预测.而由于各种原因，在学生综合素质评估中这种不完整的例子集普遍存在，目前还缺乏对具有不完整例子情况的针对性研究.朴素贝叶斯网络聚类适合于进行这类情况的识别和预测，这种聚类技术不仅在例子少或例子残缺时能够进行有效的学习和预测，甚至没有例子也可归纳出分类规则.经典的朴素贝叶斯网络聚类［6］是结合朴素贝叶斯网络与EM（expectation-maximization）算法进行的聚类，其中的条件密度估计一般选择高斯函数.由于EM算法是对分布参数的局部贪婪（greedy）寻优，因此对初始值敏感，易于陷入局部极值，参数迭代还可能收敛到并非似然函数极值的参数空间的边界，从而产生欺骗收敛，这可能导致聚类结果出现极端情况（类值聚集在少数类）.

本文针对学生综合素质评估需求和经典朴素贝叶斯网络聚类存在的问题，结合朴素贝叶斯网络结构和Gibbs sampling［7］进行层次聚类，建立层次朴素贝叶斯网络聚类（简记为HNBC）方法，能够有效避免使用EM算法所导致的局部最优问题，并且将HNBC方法用于学生综合素质评估还具有鲁棒性、灵活性和可扩展性等特点.为检验HNBC方法的可靠性，使用国际标准数据进行了预测准确率实验与分析.

用C，X1，…，Xn表示类变量与属性变量；c，x1，…，xn是具体的取值；D表示数据集；N是数据集中的记录数量，其中前N＊个记录具有类标签，后N－N＊个记录没有类标签.

1 HNBC结构和过程

HNBC是在聚类结构的基础上，实现聚类方法的过程.层次聚类可以具有多个层次，依据学生综合素质评估特点，本文只研究具有两个层次的聚类问题.下面给出两个层次的聚类结构和聚类过程.

1.1 HNBC结构

结构是聚类的基础，根据结构来确定联合概率的分解形式和参数布局.标准的朴素贝叶斯网络聚类采用星形结构，HNBC的结构是星形结构的复合，因此，可将其分解为一些相互关联的星形结构，也就是HNBC可分解成具有层次顺序的一系列朴素贝叶斯聚类.两个层次的HNBC结构如图1所示.

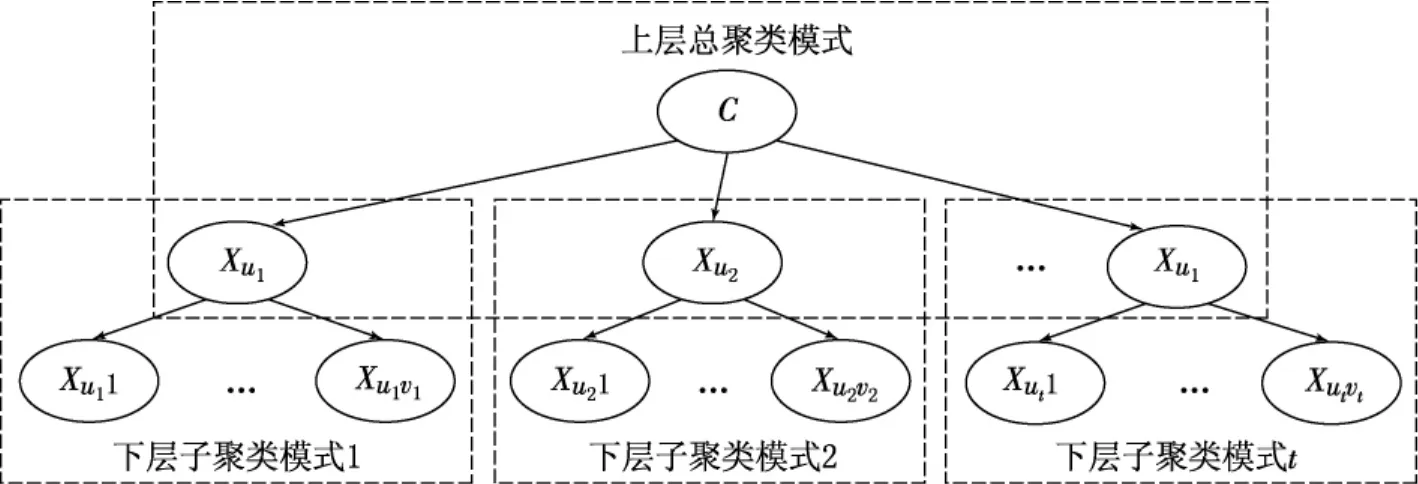
图1 两层次HNBC结构

1.2 HNBC过程和特征

具有两个层次的HNBC由两个聚类阶段构成：一个是下层子聚类；另一个是上层总聚类.首先进行下层子聚类，在下层子聚类预测结果的基础上再进行上层总聚类，最终得到待预测变量的值.

（1）聚类过程

在HNBC的上下两个层次中，下层子聚类是依据Xui1，…，XuIvi（i＝1，…，t）通过聚类预测得到XuI的过程，其中Xui1，…，Xuivi是属性，有对应的数据，Xui是类，需要进行聚类预测；上层总聚类是在下层子聚类预测结果的基础上而进行的聚类，即根据X1，…，Xt通过聚类确定C的过程.X1，…，Xt都是离散指标，它们的数据是下层聚类的结果，上层聚类预测的结果便是所需要的最终结果.

（2）聚类特征

HNBC非常灵活.聚类结构中的叶子结点（如图1中的Xui1，…，Xuivi）既可以是离散属性，也可以是连续属性.在局部的朴素贝叶斯聚类中，属性结点可以是叶子结点，也可以是中间非叶子结点，当然如果是非叶子结点，需要先进行下层聚类，以确定这些非叶子结点对应变量的值.

（3）聚类的可扩展性

在图1给出的两层次HNBC模型中，Xuivi是树的叶子结点，也可以对模型进行扩展，扩展后的Xuivi不再是叶子结点，而是中间结点.既可以进行完全扩展（所有叶子节点都扩展），也可以进行部分扩展（只扩展部分叶子结点），根据实际情况而定.也就是，一个非根结点，既可以表示一个变量，也能够代表一个朴素贝叶斯聚类模型，还可以是HNBC模型.但扩展的层数不宜太多，多层次聚类可能会降低预测的可靠性，因为存在层次误差累计效应.

2 HNBC方法

由于HNBC包含两个层次的聚类，上层聚类（离散属性聚类）所采用的方法可以看做是下层聚类（混合属性聚类）的特殊情况，因此，只给出下层混合数据聚类方法.为表述的方便，属性和类变量仍用X1，…，Xn，C表示，S表示星形结构.

确定类值的方法：

依据星形结构S所蕴含的变量之间条件独立性，得到联合概率的分解式为：

其中：p（c）是类先验概率，p（xi｜c，S）是条件概率（Xi是离散变量）或条件密度（Xi是连续变量）.对给定的类数，随机初始化C的值，并对C的值进行迭代修正，直到迭代趋于稳定.在每一次迭代中，按数据集中记录的顺序依次对类变量C的值进行修正，修正完所有记录中的C值实现一次迭代.

设在第m个记录C具有待修正值cm，Xi的值为xmi，＾cm表示cm经过修正后的值，变量C的可能取值为c1，…，crc.用D（k－1）表示第k次迭代修正前的数据集，D（k－1）n表示第k次迭代修正中对cm修正后的数据集，D（k）表示第k次迭代修正后的数据集.

对于离散属性Xi，只需采用最大似然方法估计（使用频率估计概率）属性条件概率即可.

对于连续属性Xi，使用高斯函数估计属性条件密度，即

3 学生综合素质评估

基于HNBC方法进行学生综合素质评估，首先需要建立指标体系，然后依据指标体系确定聚类结构，结合聚类结构和Gibbs sampling才可进行聚类.

3.1 指标体系

采用三级指标体系，当然模型同样适合于多级指标体系，下面给出一个可用于学生综合素质评估的指标体系.

（1）一级指标

学生综合素质等级（C），共4个级别：A级（高）、B级（较高）、C级（一般）和D级（较低）.

（2）二级指标

学生综合素质所属的二级指标是：知识结构（X1）、认知结构（X2）、人格形成（X3）.它们都分三个等级，分别为：A级（好）、B级（中）和C级（差）.

（3）三级指标

知识结构所属的三级指标是：概念学习（X11）、规则掌握（X12）、问题解决（X13）.

认知结构所属的三级指标是：输入能力（X21）、存储能力（X22）、加工能力（X23）、内部动力（X24）、外部动力（X25）、大认知策略（X26）、中认知策略（X27）、小认知策略（X28）.

人格形成所属的三级指标是：责任心（X31）、自信心（X32）、独立性（X33）、刻苦精神（X34）、忍耐力（X35）、经受挫折能力（X36）、融入社会能力（X37）.

第三级指标既可以是离散指标，也可以是连续指标，根据实际情况而定，在三级指标的下面还可以扩展出四级指标，对多级指标的聚类预测方法与三级指标类似.

3.2 HNBC结构

根据上面的学生综合素质评估指标体系可得到HNBC结构如图2：

图2 用于学生综合素质评估的HNBC结构

基于聚类结构和历史数据进行概率和密度估计，从而得到用于学生综合素质评估的HNBC模型，输入学生综合素质的最新信息通过聚类运算便可获得该学生的综合素质等级.

3.3 HNBC预测可靠性实验与分析

在UCI机器学习数据仓库［8］中选择10个分类数据集，只保留不足4%的类标签，对去除类标签的记录分别进行分类和聚类预测，并将预测结果与真正的类标签进行比较获得预测准确率，情况如表1所示.其中NBCA，CPA和PI分别表示朴素贝叶斯网络分类器的分类准确率（naive Bayesian network classing accuracy）、聚类预测准确率（clustering prediction accuracy）和提高百分率（percentage increase）.

表1 预测准确率比较

根据表1中的数据可以计算出，NBCA的平均聚类预测准确率是64.91%，CPA的预测准确率是83.88%，平均提高幅度是29.22%.可见CPA方法更加准确，将其用于学生综合素质评估，其评估结果的判断也将更加可靠.

4 小结

本文根据学生发展的特点，建立了一种学生综合素质评估的层次朴素贝叶斯网络聚类模型，其中的三级指标可以是离散指标，也可以是连续指标.模型对例子数量没有具体要求，甚至在没有例子的情况下也能够提炼出规则进行识别和判断，尤其适合于大量学生的一次性综合素质评估.这种模型在评估过程中还具有鲁棒性、灵活性和可扩展性等特点，并且能够广泛用于其他领域的评估.

［1］ 支敏，卢云辉.基于 AHP的大学生综合素质评估［J］.贵州民族学院学报：哲学社会科学版，2006，4：168-171.

［2］ 胡习文.基于FNN的智能学生综合素质评估模型研究［J］.武汉理工大学学报：信息与管理工程版，2007，29（3）：103-107.

［3］ 黄侨，林阳子，任远.基于关联度的预应力混凝土梁桥综合评估方法［J］.武汉理工大学学报，2007，29（7）：13-17.

［4］ 辛枫冬，赵国杰.企业领导者隐性知识结构的模糊综合评判［J］.统计与决策，2010，26（2）：174-176.

［5］ 胡勇，吴少华，胡朝浪.信息系统风险灰色评估方法［J］.计算机应用研究，2008，25（8）：2477-2479.

［6］ CHEESEMAN P，KELLY J，SELF M，et al.Autoclass：a Bayesian classification system［C］／／LAIRD J，SAN MATEO.Proceedings of the 15th International Conference on Machine Learning，CA：Morgan Kaufmann，1988，54-64.

［7］ GEMAN S，GEMAN D.Stochastic relaxation，gibbs distributions and the Bayesian restoration of images［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1984，6：721-742.

［8］ MURPHY S L，AHA D W.UCI repository of machine learning databases［EB／OL］.［2010-10-15］.http：／／www.ics.uci.edu／～mlearn／MLRepository.Html.

The clustering method of hierarchical naive Bayesian network for student comprehensive quality assessment

LI Lan-chun1，WANG Shuang-cheng2，WANG Hui3
（1.School of Foreign Studies，Shanghai Lixin University of Commerce，Shanghai 201620，China；
2.School of Mathematics and Information，Shanghai Lixin University of Commerce，Shanghai 201620，China；
3.School of Information Engineering，The Central University for Nationalities，Beijing 100081，China）

The student comprehensive quality assessment is one effective way for testing student overall level of development.A hierarchical naive Bayesian network clustering method is developed for student comprehensive quality assessment based on the features of student comprehensive quality assessment and the problems in existing assessment methods.This method not need many examples.Even if no example，it can also extracte rules and do prediction.The experimental results show that the method has very good prediction accuracy so that it will be more reliable to assess student comprehensive quality.

student comprehensive quality assessment；assessment；hierarchical naive Bayesian network；clustering

TP 181

520·20

A

1000-1832（2011）03-0049-05

2010-12-05

国家自然科学基金资助项目（60675036）；教育部人文社科基金资助项目（10YJA630154）；上海市教委重点学科建设项

目（J51702）；上海市教委科研创新重点项目（09zz202）.

李兰春（1959—），女，讲师，主要从事教育评估理论与方法研究；王双成（1958—），男，博士，教授，主要从事计算机智能技术与应用研究；王辉（1961—），男，教授，主要从事决策支持技术与应用研究.

陶 理）