简单可求长曲线上的曲线积分

毛战军

(长江大学一年级工作部，湖北荆州 434023)

简单可求长曲线上的曲线积分

毛战军

(长江大学一年级工作部，湖北荆州 434023)

通过讨论简单可求长曲线上的曲线积分，减弱曲线积分计算所需的条件，拓广曲线积分计算方法应用的范围.

光滑曲线;简单可求长曲线;曲线积分

关于曲线积分定义的阐述及曲线积分的计算，都要求所讨论的曲线弧是光滑的，即要求曲线弧的参数方程x=φ(t)，y=ψ(t)，t∈［α，β］满足x=φ(t)，y=ψ(t)在［α，β］上有连续的一阶导数，且φ'2(t)+ψ'2(t)≠0.曲线积分并非只有在曲线弧光滑时才能够进行计算.

1 第一型曲线积分的定义与计算的充分条件

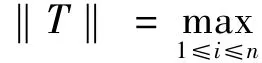
在第一型曲线积分的定义中，并没有强调所讨论的曲线弧为光滑曲线弧，只是要求所讨论的曲线弧为平面上可求长度的曲线弧，而在曲线积分计算的充分条件中，却要求曲线弧是光滑的.可以猜想:曲线光滑不是曲线积分计算的必要条件.

2 引理与结论

引理1设Γ=是Rn中简单可求长曲线，f(x，y)在Rn中包含Γ的一个开区域Ω内连续，则f(x，y)在Γ上的第一类曲线积分存在，且使得Γ的任意分割T:A=A0，A1，…，Am=B，当d(T)=时，f(x，y)在内折线上的积分收敛于f(x，y)在Γ上的积分［2］.从引理中可以看到，只要满足引理的条件，f(x，y)在内折线上的积分收敛于f(x，y)在Γ上的积分，则可以考虑下面的结论.

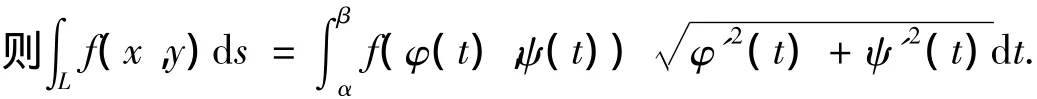
证明 取L的任意分割T:A=A0，A1，…，An=B，得到内折线A0A1…An，则Ai=(φ(ti)，ψ(ti))，i=0，1，…，n，线段Ai－1Ati的长度为

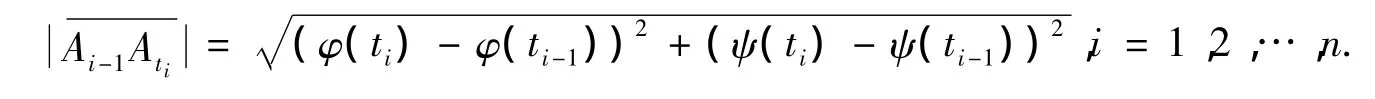
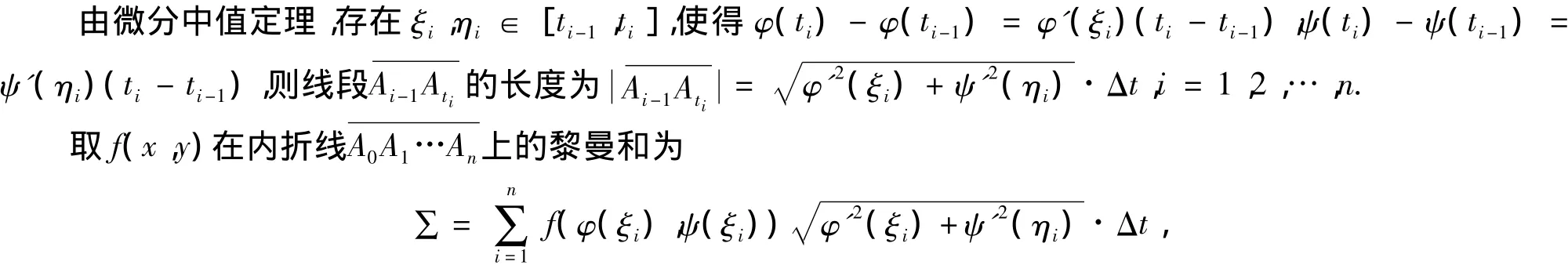
则由引理得，当max{Δti}→0时，∑→∫Lf(x，y)ds.取和式

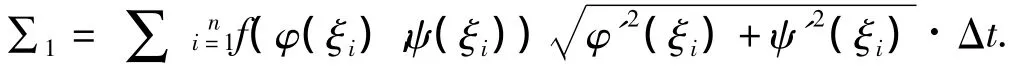
由φ'(t)，ψ'(t)在区间［α，β］上黎曼可积，则φ'2(t)+ψ'2(t)在区间［α，β］上黎曼可积是x的连续函数，则φ'2(t)+ψ'2(t)在区间［α，β］上黎曼可积，则当max{Δti}→0时，

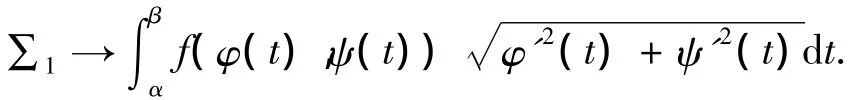
可以证明定理2是成立的，由此可知在讨论曲线积分的时候，曲线弧光滑这一条件并不是必要的.在简单连续曲线L:x=φ(t)，y=ψ(t)，t∈［α，β］上，如果φ(t)，ψ(t)在［α，β］上可微，不需要φ'(t)，ψ'(t)在区间［α，β］上连续，只需要φ'(t)，ψ'(t)在区间［α，β］上黎曼可积，则曲线积分的计算公式依然是成立的.

3 结束语

在一般工程应用中讨论曲线积分时，大多要求所涉及的曲线弧是光滑的，这是利用定积分计算曲线积分的充分条件.定理2减弱了计算所需的条件，应用的范围更广泛.

［1］ 华东师范大学数学系.数学分析:下册［M］.3版.北京:高等教育出版社，2001.

［2］ 黄玉民，李成章.数学分析:下册［M］.北京:科学出版社，1999:349－350.

Curvilinear Integral on Simple Rectifiable Curve

MAO Zhan-jun

(Freshman Education Department，Yangtze University，Jingzhou434023，China)

Through discussion on curvilinear integral on simple rectifiable curve，weakened the condition of calculating curvilinear integral，and extended the application scope of calculation methods for curvilinear integral.

smooth curve;simple rectifiable curve;curvilinear integral

O174.1

A

1007－0834(2011)04－0020－02

10.3969/j.issn.1007－0834.2011.04.007

2011－07－21

毛战军(1970—)，男，湖北仙桃人，长江大学一年级工作部讲师.