定积分不等式证明方法的研究

张 瑞，蒋 珍

(1.宝鸡文理学院数学系，陕西宝鸡 721013;2.中原工学院电子信息学院，河南郑州 450011)

定积分不等式证明方法的研究

张 瑞1，蒋 珍2

(1.宝鸡文理学院数学系，陕西宝鸡 721013;2.中原工学院电子信息学院，河南郑州 450011)

通过利用定积分的定义，已知不等式、泰勒公式、积分中值定理、辅助函数法、二重积分等方法研究了有关定积分不等式的证明方法及规律.

定积分;积分性质;中值定理;积分不等式;泰勒公式

0 引言

含定积分的不等式一般可以利用已知不等式如柯西—施瓦兹不等式、积分中值定理、辅助函数等方法来证明.本文归纳并列举了几种定积分不等式的证明方法，主要有利用已知不等式、泰勒公式、积分中值定理以及辅助函数法等方法.

1 利用定积分的定义

主要是利用定积分的定义，通过将闭区间［a，b］分割、求和并求当T→0时和的极限，比较积分大小则可通过比较和的极限来实现.

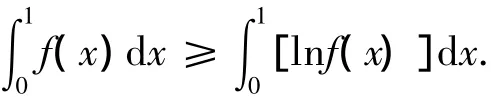
分析题中所给的已知条件较少，在这种条件下利用定积分的定义将区间分割求极限比较简单.

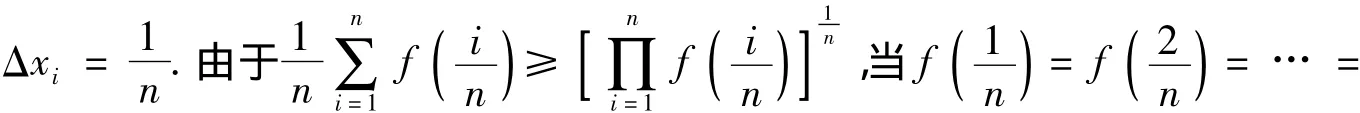
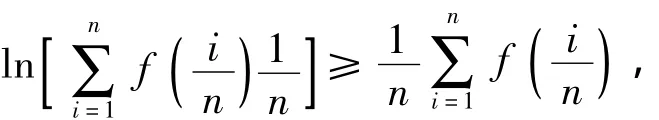
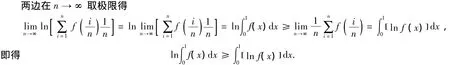
2 利用柯西—施瓦兹不等式

分析在此题中出现了f2(x)，g2(x)因此可以联想到施瓦兹不等式.

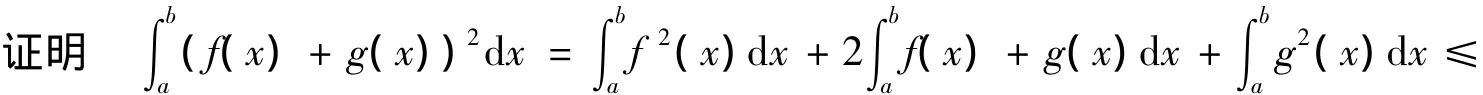
3 利用泰勒公式

如果函数f(x)的二阶和二阶以上导数存在且有界，可利用泰勒公式来证明.

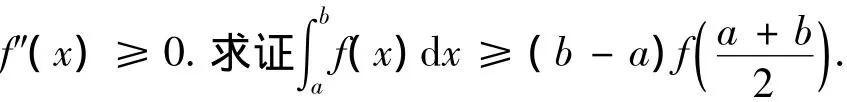
4 利用积分中值定理

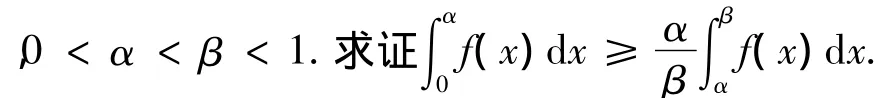
分析由已知条件可知函数具有连续单调性，可考虑使用积分第一中值定理来证明.

5 构造辅助函数法

当已知被积函数连续，并没有告知可导时，通常用此法最为方便，主要利用辅助函数的单调性证明.只需做辅助函数将结论中的积分上(下)限换成变量，移项使不等式一端为0，则另一端即为所作的辅助函数.

6 利用凸函数的性质

如果函数f(x)在［a，b］上连续，在(a，b)内具有一阶导数和二阶导数，那么

7 利用二重积分

当被积函数积分区间相同，利用变量的对称性及二次积分转化为二重积分证明可以带来很大方便.

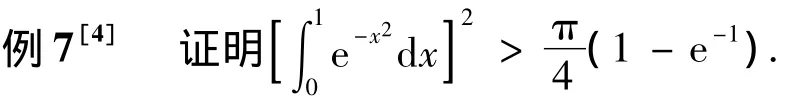
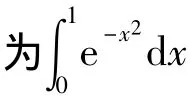
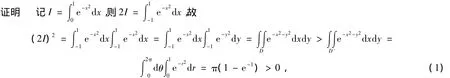
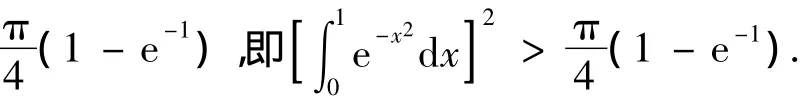
［1］ 华东师范大学数学系.数学分析［M］.3版.北京:高等教育出版社，2001.

［2］ 复旦大学数学系.数学分析［M］.2版.北京:高等教育出版社，1983.

［3］ 同济大学数学系.数学分析［M］.6版.北京:高等教育出版社，2007.

［4］ 辛小龙，刘新平.高等数学［M］.北京:高等教育出版社，2007.

On Proof Method of Definite Integral Inequalities

ZHANG rui1，JIANG Zhen2

(1.Department of Mathematics，Baoji University of Arts and Sciences，Baoji721013，China; 2.College of Electronic and Information，Zhongyuan University of Technology，Zhengzhou450011，China)

Researches definite integral inequality proof methods and rules by such methods as definition of definite integral，known inequality，Taylor formula，and integral mean value theorem，method of auxiliary function and double integral method.

definite integral;integral property;mean value theorem;integral inequality;Taylor formula

O172.2

A

1007－0834(2011)02－0017－03

10.3969/j.issn.1007－0834.2011.02.006

2010－12－05

河南省科技厅自然科学基金项目(2010A110011);宝鸡文理学院重点项目(ZK09129)

张 瑞(1979—)，女，陕西西安人，宝鸡文理学院数学系教师.