多阶段决策过程最优化问题研究

刘义山，李骥昭

(平顶山工业职业技术学院文教部，河南平顶山 467001)

多阶段决策过程最优化问题研究

刘义山，李骥昭

(平顶山工业职业技术学院文教部，河南平顶山 467001)

讨论了动态规划的基本原理和基本方法，通过解决建设汽车样板店的一个三阶段决策问题说明其应用.

多阶段决策;单阶段决策;动态规划;优化算法;最优决策

0 引言

在实践中，常常会遇到这样的决策问题［1－4］:由于过程的特殊性，可以将决策的全过程依据时间或空间划分为若干个相互联系的阶段.动态规划方法的关键是将多阶段的决策问题变换成一系列的单阶段问题，并逐一求解.多阶段的决策过程很难直观地描述，本文通过一个实例来说明动态规划解决多阶段决策问题的方法和过程.

1 多阶段决策问题探讨

例如，某汽车公司准备在华北、华东、华南3个地区建立标准的四位一体的汽车销售样板店.由于资金有限，只能建3个样板店.为了达到公司销售收入最大的目的，公司不限制在各个地区建立样板店的数目.因此，每个地区最多建3个样板店.每个地区预期创造的销售收入见表1.

表1 每个地区可能创造的销售收入Tab.1 Possible sale revenue created by each area

从表1中可以看出，如果没有在华北和华东地区建样板店，那么这两个地区的销售收入为0.如果没有在华南地区建样板店，华南地区仍可以通过订购系统获得每月2万元的销售收入.这个问题的目标函数是在建样板店的个数有限的条件下，如何建店使公司的销售收入总额最大.它的数学表达形式是

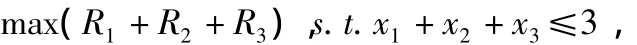
其中R1，R2，R3分别代表华北、华东和华南的销售收入，x1，x2，x3表示决定在这3个地区建立样板店的数目.

为了解决这个问题，首先定义一下阶段.将在华北地区建多少样板店作为问题第一阶段的决策，将在华东地区建多少样板店作为问题第二阶段的决策，将在华南地区建多少样板店作为问题第三阶段的决策.假设这就是决策的先后顺序.显然这是一个三阶段决策过程的最优化问题.用动态规划来解这个问题，就是要把这个三阶段的决策问题化为3个较容易解决的单阶段决策问题.每个单阶段的决策是整个决策过程的一个环节，因为它不仅决定该阶段的效果(销售收入)，还影响到下阶段的初始状态(剩余的建店指标).在求解该问题过程中，从最后一个阶段开始逐阶段反向递推，找到销售收入最大的方案，当递推到第一阶段时，也就找到了全过程的最优方案.这种从后向前逆推的方法叫逆序解法.

1.1 第三阶段决策

将在华南地区建多少样板店作为问题第三阶段的决策.在动态规划中假设第三阶段的决策是决策过程中的最终决策，因此，如果将在华东、华北地区建样板店作为规划的第二阶段和第一阶段，那么在华南地区建几个样板店的决策是建立在另两个地区已决定建店的个数的基础上的.第三阶段可能的建店方案如表2，其中S3表示第三阶段剩余的建店指标，x3表示决定建店的个数.

表2 第三阶段可能的建店方案Tab.2 Possible scheme of building stores in phase 3

从表2可以看出，如果3个样板店已经决定建在另外两个地区，那么第三阶段剩余的建店指标为0，决策只能是在华南地区不建店，该地区的销售收入为2万元/月.如果已决定在另外两个地区建2个店，那么第三阶段剩余的建店指标为1，就要考虑在华南建1个店或不建店;同样，如果在第三阶段剩余的建店指标为2个，就要决定第三阶段该建0个、1个或2个店;如果在第三阶段剩余的建店指标为3个，就要决定在第三阶段建0个、1个、2个或3个店.

表2中有动态规划中的常用符号S3，x3，R3.S3为第三阶段的可达状态的集合，指当一、二阶段做出建店决策后第三阶段到最后阶段(仍为第三阶段)剩余的建店指标.在这个问题中，可达状态是指从每个阶段到最后阶段剩余建样板店的指标.从表2中可以看出，第三阶段有4个可达状态，也就是当一、二阶段决策后，第三阶段剩余的建店指标可能为0、1、2、3.x3代表在不同的状态下第三阶段的决策.R3表示在不同的决策下，第三阶段(华南地区)获得的销售收入.

动态规划的下一步是决定每个可达状态下的最优决策.在这个问题中，每个状态下的最优决策就是获得的销售收入最大.每个状态下的最优决策如表3所示.

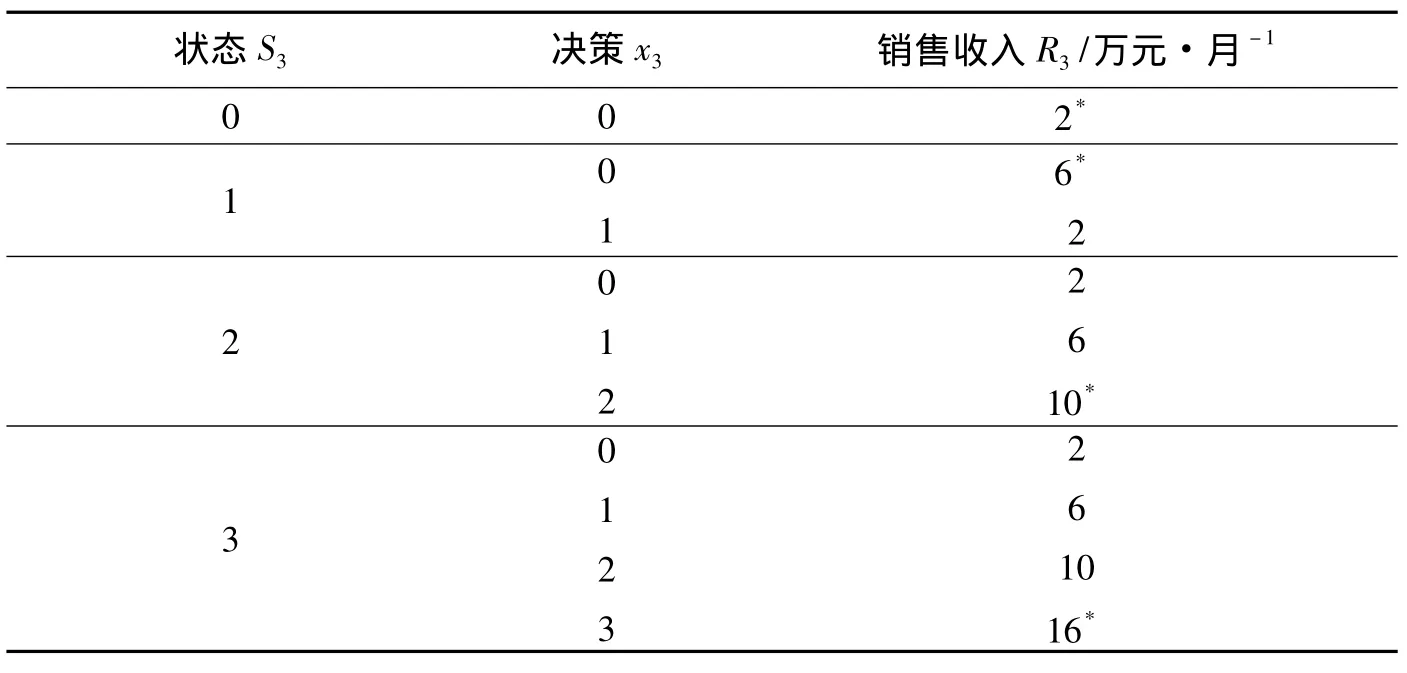
表3 每个状态下的最优决策Tab.3 Optimum decision in each status

第三阶段各个状态下的最优决策要继续运用到上一阶段的决策中.

1.2 第二阶段决策

既然第三阶段最优决策已知，进入上一阶段决策，决定如何在华东地区建店.第二阶段的可达状态和可选的决策与第三阶段基本相同.但是，每种状态下的最优决策的选择就有不同.第二阶段的可达状态和可选决策如表4所示，R2+R3为二、三阶段的销售总收入，R3为第三阶段最优决策下的销售收入.

表4中1、2、3列与表2数据求法相同，S2表示第二阶段的可达状态的集合，指当第一阶段作出建店决策后第二阶段到最后阶段(第三阶段)剩余的建店指标.x2和R2代表在不同的状态下第二阶段的决策和销售收入.R3第4、5列反映的是在决定第二阶段的建店数目的条件下，第三阶段剩余建店的指标和相应第三阶段的最优决策.第6列表示二、三两个阶段的销售收入.从4、5列可以看出，第三阶段剩余的建店指标是第一阶段决策后从第二阶段到最后阶段剩余的建店指标和第二阶段决定建店的个数的函数.例如，如果从第二阶段到最后阶段(第三阶段)剩余建店的指标为1，而且决定在第二阶段华东建店的个数为0，那么第三阶段剩余建店的指标为1.

多阶段决策问题的各个阶段间的相互关系可以定义为状态转移方程.状态转移方程是确定由一个状态到另一个状态的演变过程.对于第k+1阶段，该阶段的状态Sk+1与上阶段的状态Sk的状态转移规律为Sk+1=Sk－xk.例如，从第二阶段到最后阶段剩余建店的指标状态S2为3，而决定在华东建店的个数x2为2，那么第三阶段到最后阶段(就是第三阶段)剩余的建店指标状态S3=S2－x2=1.

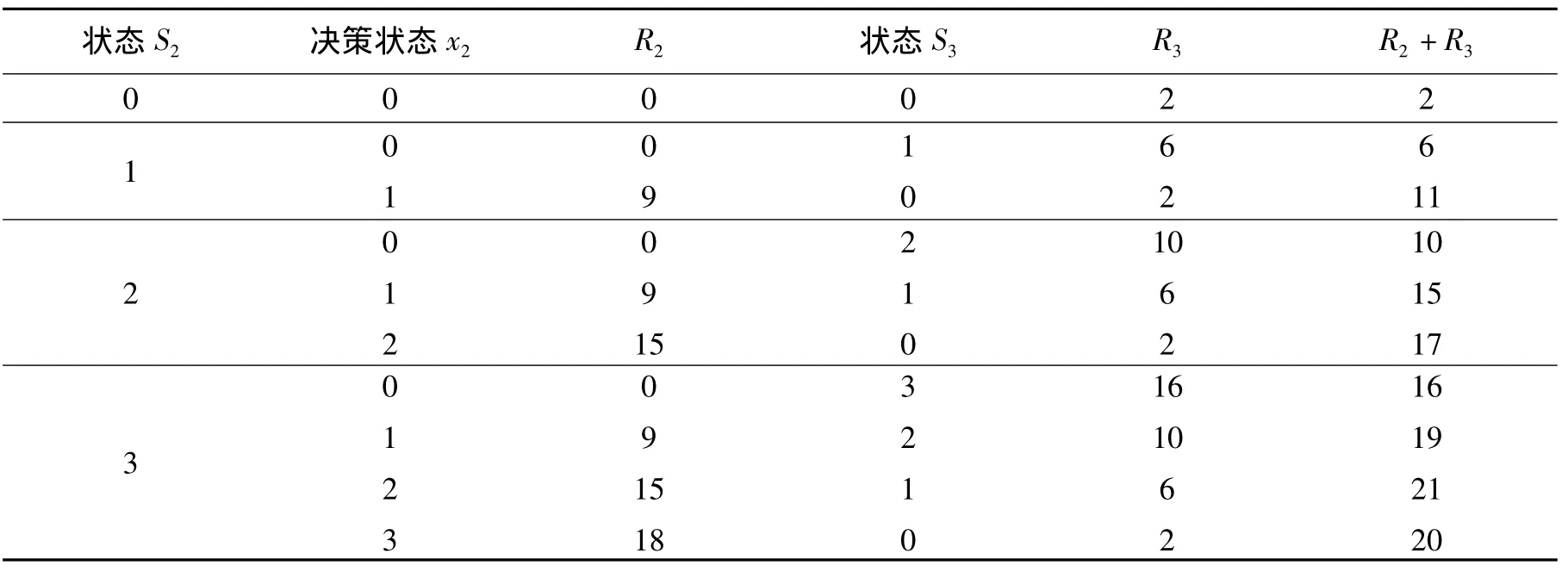
表4 第二阶段的可达状态和可选决策Tab.4 Accessible status and optional decision in phase 2

然后，再计算在第二阶段每个可达状态下因第二阶段和第三阶段的决策产生的两个阶段的销售总收入R2+R3，并选取每个状态下第二阶段和第三阶段销售收入最大的决策为该状态下的最优决策，如表5所示，R3为第三阶段最优决策下的销售收入，状态S2为从第二阶段到第三阶段剩余的建店指标，状态S3为第三阶段剩余的建店指标.

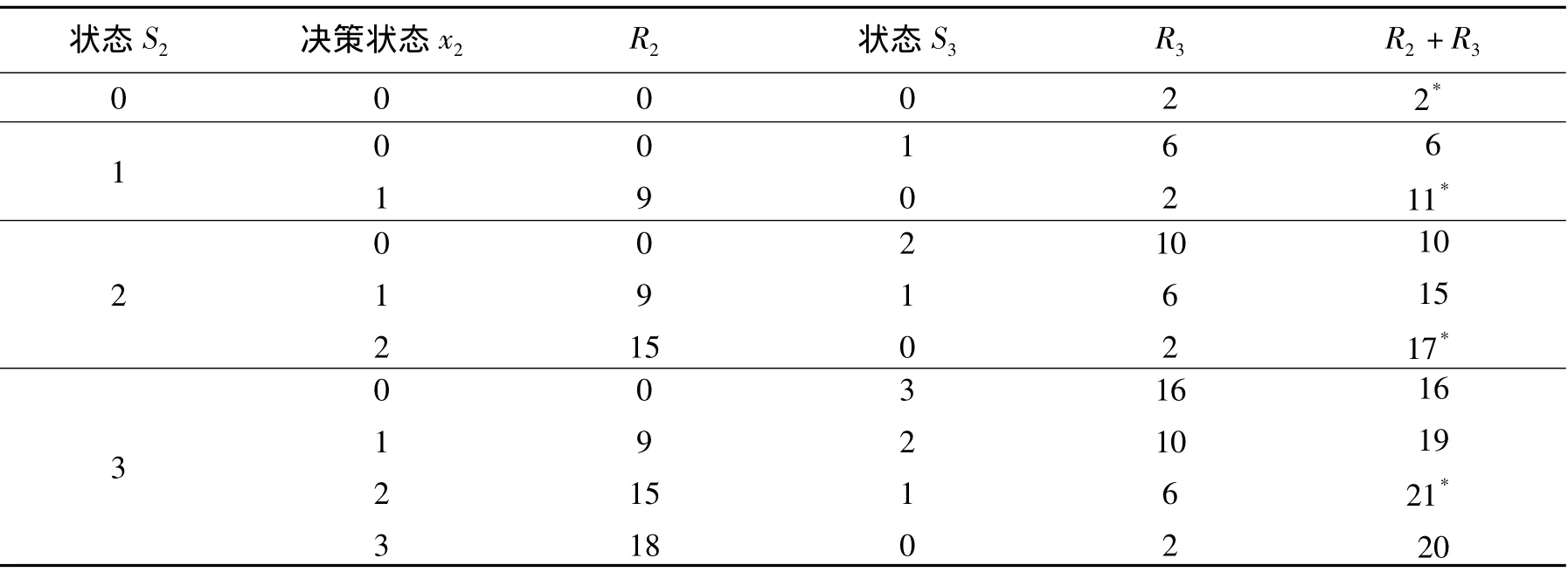
表5 最优决策的计算Tab.5 Calculation on optimum decision

1.3 第一阶段决策

现在考虑第一阶段在华北地区建样板店，由于这是决策过程中首先决策的第一阶段，所以该阶段到第三阶段剩余的建店指标为3个.决定在此建店的个数可以为0、1、2和3个.这时，第二阶段的可达状态就由第二阶段与第一阶段的状态转移方程S2=S1－x1决定.

比如，表6中状态S1为第一阶段到第三阶段剩余的建店指标，决策x1决定建店的个数，R1为华北销售收入，R2+R3为第二阶段最优决策下的销售收入，R1+R2+R3为三个阶段的销售总收入.因为S1=3，如果决定在华北建店的个数x1=1，那么从第二阶段到第三阶段剩余建店的指标为S2=2.从表5中得出，S2=2状态下的最优决策是决定在华东建两个样板店，在华南不建店，华东和华南两个地区的销售收入为17万元/月.华东和华南两个地区的销售收入加上华北地区建的1个样板店的销售收入7万元/月，那么3个地区的总收入为24万元/月.

第一阶段的最优决策是使3个地区的销售总收入最大的决策，如表7所示，状态S1为第一阶段到第三阶段剩余的建店指标，决策x1为决定建店的个数，R1为华北销售收入，状态S2为第二阶段到第三阶段剩余的建店指标，第二阶段最优决策下的销售收入R2+R3，三个阶段的销售总收入R1+R2+R3.

再按照计算的顺序反推回去(称为回代或反向追踪)，可以找到使3个阶段的销售总收入达到最大的最优策略.如表8所示.

表6 使3个地区的销售总收入最大的决策方案Tab.6 Decision scheme of maximizing total sale revenue of 3 areas

表7 第一阶段的最优决策Tab.7 Optimum decision of phase 1

表8 使3个阶段的销售总收入达到最大的最优策略Tab.8 Optimum decision of maximizing total sale revenue in 3 phases

2 结束语

动态规划把困难的多阶段决策问题变换成一系列相互联系的比较容易的单阶段问题，一个个地求解，这是经典优化方法难以做到的.动态规划是考察解决问题的一种途径，而不是一种特殊的算法，不像线性规划那样有统一的数学模型和算法.动态规划可以解决各类多阶段决策问题，不像其他方法局限于解决某一类问题.以上运用动态规划的方法解决了建设汽车样板店的一个三阶段决策问题，解决问题的思路和步骤可以运用到各种动态规划的问题中.

［1］ 张维迎，叶民强.博弈论与信息经济学［M］.上海:上海人民出版社，1996.

［2］ 邓成梁，马致山，张文杰.运筹学的原理和方法［M］.武汉:华中理工大学出版社，1996.

［3］ 施锡铨，韩其恒.博弈论［M］.上海:上海财经大学出版社，2002.

［4］ 谢识予.经济博弈论［M］.上海:复旦大学出版社，2002.

Research on Optimization Problem of Multi-phase Decision Process

LIU Yi-shan，LI Ji-zhao

(Department of Culture and Education，Pingdingshan Industrial College of Technology，Pingdingshan467001，China)

Discussed basic principle and method of dynamic program，illustrated its application by solving a threephase decision problem of building automobile model shops.

multi-phase decision;single phase decision;dynamic program;optimization algorithm;optimum decision

O221.3

A

1007－0834(2011)02－0008－04

10.3969/j.issn.1007－0834.2011.02.003

2011－04－18

刘义山(1962—)，男，河南南阳人，平顶山工业职业技术学院文教部副教授，主要研究方向:数学教育.