坝体与库水的流固耦合分析
2011-12-25龚亚琦苏海东崔建华
龚亚琦,苏海东,崔建华
坝体与库水的流固耦合分析
龚亚琦,苏海东,崔建华
(长江科学院 材料与结构研究所,武汉 430010)
基于流固耦合分析方法,分别应用势流模式和位移模式2种流体单元模拟库水,并与传统的附加质量方法模拟库水的方法做了比较,结果显示该方法可行;相比附加质量方法,流固耦合方法与理论解更为接近,其中位移模式流体单元对单元形态要求较高。对库水截取区域的敏感性分析表明,流体区域选取3~5倍坝高可以得到较为满意的结果。以重力坝的不同坝顶宽度为例,讨论了需要考虑库水可压缩性的条件,这些成果为后续工作奠定了基础。
流固耦合;动水压力;自振频率;可压缩性
1 概 述
坝体-库水之间的相互作用一直是水工结构动力分析中的一个重要课题。以混凝土重力坝为例,当大坝受到地震激励时,库水的作用对坝体的动力响应有着显著的影响。在地震作用下,坝体的振动带动了库水的运动,库水状态变化产生的附加动水压力,反过来又作用于坝体,影响坝体的动力特性,这种情况下,结构受到的动压力是不能事先确定的,它与结构变形密切相关,因此,这种作用具有耦合特性[1]。
坝-水耦联振动问题,最早由 Westergaard[2]在30年代提出。当时为了满足建坝过程中计算坝体上游面承受的附加动水压力的需要,提出了刚性重力坝在水平地震荷载作用下的动水压力分布公式。Westergaard公式采用刚性坝面假设,忽略了坝体的弹性变形和库水的状态对动力响应的影响,该成果方法简便、计算量小,被水工结构抗震规范所广泛采用并沿用至今。近年来,随着计算机技术的发展和各种数值计算方法的提高,坝体-库水的耦合问题可以采用流固耦合方法来求解,通过建立流体单元模拟库水运动状态并考虑实际的边界条件,对坝-水系统作更为真实的仿真模拟。
2 坝体-库水数值模型
2.1 附加质量公式
1933年,Westergaard将坝面动水压力分布近似地用抛物线来表示,根据力矩相等条件,给出了水平地震动激励下,具有铅直上游面的刚性重力坝沿坝高的坝面动水压力分布,即
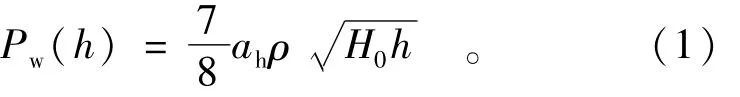
式中:Pw(h)为水深h处的动水压力;ah为水平设计地震加速度代表值;ρ为水体质量密度;H0为库水深。
动水压力的特点与惯性力相似,所以可以用附着在坝面的一定质量的水体来代替水的动力学效应。为了适用任意形状的坝体和河谷形状,1982年,Clough[3]推广了韦斯特伽特公式,建立了适用于有限元分析的广义质量表达式
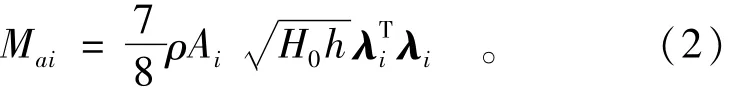
式中:Mai为附加质量;λi是坝面点的法向矢量;Ai为该点在坝面上的隶属面积。
有限元中,流固耦合的求解有2种求解模式:①势流模式,流体采用欧拉坐标系下的标量函数作为场变量,而固体采用拉格朗日坐标系下的位移作为场变量;②位移模式,应用位移流体单元,流体和固体均采用位移作为场变量,其好处是结构和流体具有相同的自由度,自动满足流固耦合边界上的变形协调条件。
2.2 势流模式

对于势流单元,基于流体无旋、无粘和均质假定,可以得到以压力P为目标的波动方程为流体中的声速,kw为流体体积模量,ρ为流体的密度。
不考虑水体可压缩性时,(3)式简写为▽2P=0,其中,边界条件如下。
流固交界面:

式中:n为坝体-库水交界面的法向;¨Un为法向加速度。
自由液面边界,忽略水表面重力波影响:

采用Galerkin法分别建立库水和坝体的动平衡方程,并组合成统一的矩阵形式:

式中:U和P分别为位移和动水压力;¨U和¨P分别为位移和动水压力对时间的二阶导数;U和P分别为位移和动水压力对时间的一阶导数;M,C,K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵;M′,C′,K′分别为流体的质量矩阵、阻尼矩阵和刚度矩阵;Q为坝-库交界面上的耦合矩阵;F为结构荷载向量。从公式(1)来看,由于流体的引入,合成矩阵为非对称的。
2.3 位移模式
对于位移流体单元,流体单元与固体一样采用位移模式,可以直接用结构有限元方法来建立流体单元物理方程为[4,5]
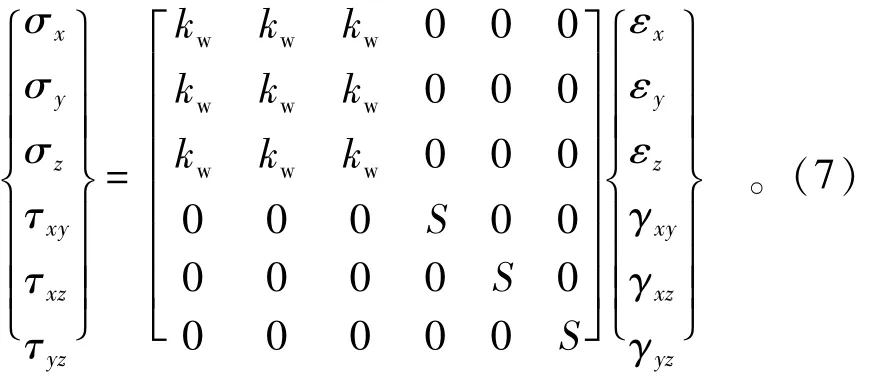
式中:σx,σy,σz分别为流体单元的正应力;εx,εy,εz分别对应为流体单元的正应变;τxy,τxz,τyz分别为流体单元的剪应力;γxy,γxz,γyz分别对应为流体单元的剪应变;S表示流体的等效剪切模量;kw为流体的体积模量。
与固体单元不同的是,流体与流体之间,以及流体与固体单元之间并不传递剪力,仅只传递法向压力,所以物理方程中剪切模量应该为0,但这样会导致流体矩阵的奇异[6],为了简便起见,可以将流体设置为相对体积模量很小的一个数值[5],如kw·10-9。
为了检验上述方法的可靠性,下面将用具体算题加以讨论。
3 数值算例
3.1 悬梁一侧受液体作用时的自由振动
为与理论解对比,本文选用文献[1]中悬臂梁一侧受液体作用时的自由振动的耦联系统的经典算例(如图1所示)。
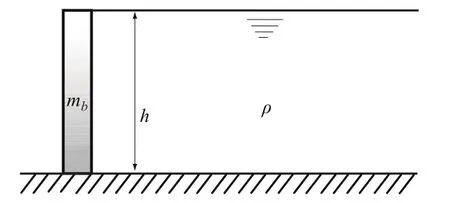
图1 悬臂梁与液体耦联系统Fig.1 Fluid-solid coupling system of cantilever beam and water
模型中梁宽1 m,流场与梁等高(h=10 m),梁的密度为mb,梁的弹性模量为20 GPa,泊松比为0.2;流体密度 ρ取 1 000 kg/m3,流场在顺流方向截取到距梁30 m的区域范围。理论解[1]表明,湿模态频率与 ρh/mb的值有关,因此计算过程中,ρh/mb分别取为0.5,1,2,3。不考虑水体的可压缩性,分别采用势流模式、位移模式2种流体单元和附加质量方法,进行系统模态分析,计算有水频率如表1所示。
从表1可以看出,附加质量方法基于刚性坝面假设,计算的附加质量偏大[7],增大了系统的整体质量,因此与流固耦合方法相比,其计算出的基频偏小。
采用流固耦合方法计算的频率与理论解比较接近,相对误差在2%以内,但是随着ρh/mb的增大,流体的质量相对固体质量的比重逐渐增大,有水频率与理论级数解的相对误差有增大的趋势。
需要说明的是,采用位移模式时,计算过程中出现了很多小频率,需要预先判断结构的自振频率区间,进行过滤处理。这主要是由于流体剪切模量很小,形成了病态方程,Wilson[8]提出在计算中引入一个罚参数项,并对流体进行无旋运动限制,通过改变罚参数来解决这一问题。

表1 耦联系统中梁的基频Table 1 Natural frequency of cantilever beam in the fluid-solid coupling system
3.2 流体作用域的影响
采用流固耦合方法,流体作用域的范围直接影响计算的精度,下面,分别采用2种流体单元模式,选用实际大坝模型,对水体区域的截取范围作敏感性分析。
选取一重力坝[9],如图2所示,坝高105 m,坝顶宽10 m,坝底宽80 m,上游坝面竖直,沿坝轴线方向取宽度100 m。坝体混凝土:弹模为1.96×1010Pa,密度为 2 400 kg/m3,泊松比为0.2;水体:密度为1 000 kg/m3,水中纵波传播速度 c=1 440 m/s,水深为100 m。计算过程中,不考虑库水表面重力波和坝基的影响,分别选取不同的流体域长度:1~6倍坝高,对其数值结果的稳定性进行比较分析。由于势流模式和位移模式计算的坝体振型不尽相同,选取不同工况下相同振型对应的三阶坝体频率列于表2。
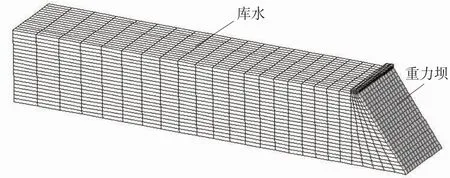
图2 重力坝-库水耦合有限元模型Fig.2 Finite element model of gravity dam-reservoir
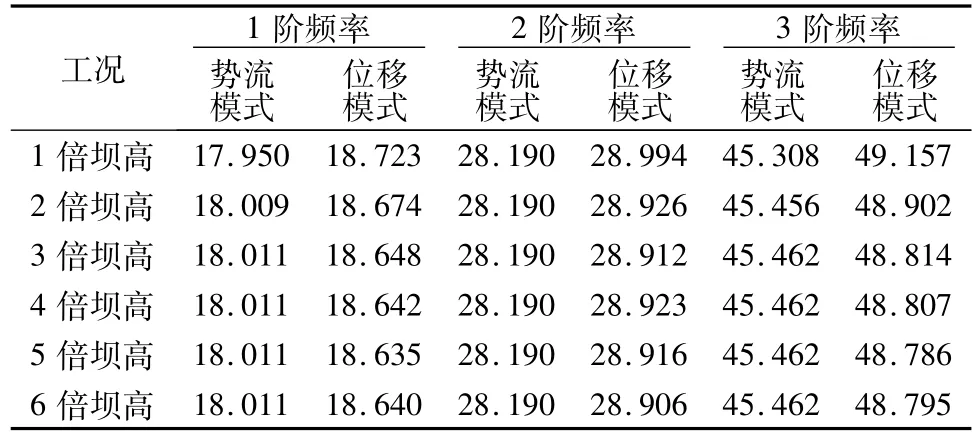
表2 不同流体域长度坝体自振频率Table 2 Natural frequencies of dam by different reservoir models with different water areas rad/s
水体区域敏感性分析表明:采用势流模式流体单元时,上游取3倍坝高可以得到稳定的数值结果;采用位移模式流体单元时,计算结果随流体区域的选择有波动,5倍坝高基本可以得到满意的结果;2种流体单元模式计算的前二阶频率相对误差在4%以内。
3.3 水体可压缩性的影响
在坝水相互作用过程中,是否可以忽略库水可压缩性影响一直是一个有争议的问题。与不考虑库水可压缩性相比,考虑库水可压缩性时的分析要复杂的多。考虑库水可压缩性的影响之后,将使得原来所需求解的拉普拉斯方程转为相应的波动方程,在求解方面增加了很大的难度。本文将从结构的角度,就库水的压缩性在坝-水相互作用中的具体影响作进一步探讨。
模型仍然选用上述重力坝模型,坝顶宽度B作为变量,分别采用不同坝顶宽度(10,20,30,40,50,60 m),比较附加质量法、不可压缩库水单元以及可压缩库水单元对结构频率振型的影响。
从图3可以看出,随着坝顶宽度的增加,坝体质量逐渐增大,流固耦合方法与附加质量方法计算的自振频率的差距越来越大,表1的结果也说明了这一点,此时用流固耦合方法计算系统的动力特性更准确。
同时,随着坝体质量的增加,结构的自振频率逐渐降低,考虑和不考虑水体可压缩性,两者计算的结果越来越接近。
图4是不同坝体弹性模量条件下,附加质量法、不可压缩库水单元以及可压缩库水单元对结构频率振型的影响。模型中坝体弹性模量(E)分别选取为10,20,30 GPa时,结构的自振频率逐渐增大,相比不可压缩库水单元,考虑库水可压缩性时求得的自振频率增加的幅度较慢。
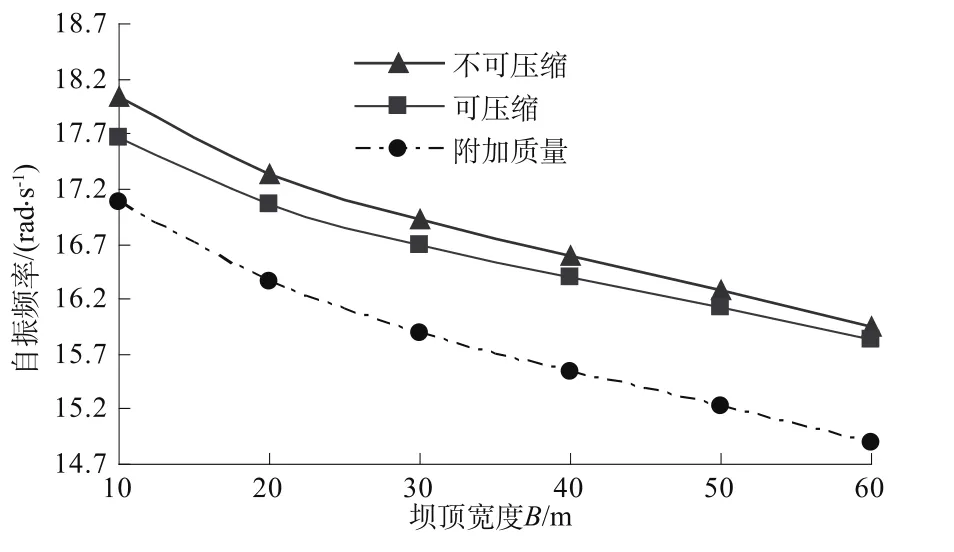
图3 不同坝顶宽度(B)对自振频率的影响Fig.3 Effect of different top dam widths(B)on natural frequency
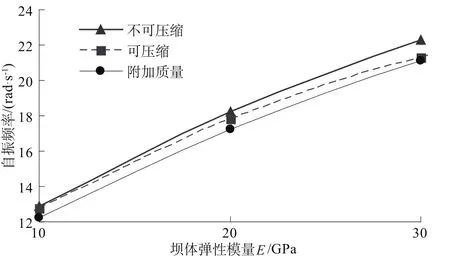
图4 不同坝体动弹性模量(E)对自振频率的影响Fig.4 Effect of different dynamic elastic moduli of dam(E)on natural frequency
对比图3和图4可看出,当结构自振频率较高时,库水压缩性对结构动力特性影响较为显著。库水可压缩性的影响还与地形、淤泥、基岩和共振频率等综合条件有关[7,9,10]
4 结 论
分别采用势流模式和位移模式2种流体单元模拟库水,并与坝体结构单元耦合模拟坝体-库水的相互作用。
(1)经典算例结果显示,流固耦合方法与理论解更为接近,采用流体单元模拟库水的方法是可行的;采用位移模式时,需要加入无旋约束,过滤小频率。
(2)库水截取区域的敏感性分析表明:流体区域选取3~5倍坝高可以得到较为满意的结果;2种流体单元模式计算的前二阶频率相对误差在4%以内。
(3)当坝体结构自振频率比较高时,库水压缩性对结构动力特性的影响较显著。
[1] 黄玉盈.结构振动分析基础[M].武汉:华中工学院出版社,1988.(HUANG Yu-ying.Structural Vibration Analysis[M].Wuhan:Huazhong University of Science&Technology Press,1988.(in Chinese))
[2] WESTERGAARD H M.Water Pressures on Dams During Earthquakes[J].Transactions of the American Society of Civil Engineers,1933,98:418-472.
[3] CLOUGH H M.Reservoir Interaction Effects on the Dynamic Response of Arch Dam[J].Proceedings of China-US Bilateral Workshop on Earthquake Engineering,1982:58-84.
[4] 李遇春,楼梦麟,尚 伟,等.大型渡槽抗震分析中流体的位移有限元模式[J].水利学报,2003,2:93-97.(LI Yu-chun,LOU Meng-lin,SHANGWei,et al.Displacement-Based Fluid Finite Element for Seismic-Resistant Analysis of Large-Scale Aqueduct[J].Journal of Hydraulic Engineering,2003,2:93-97.(in Chinese))
[5] 李遇春,楼梦麟,周 成.大型渡槽的竖向地震效应分析[J].地震工程与工程振动,2008,28(2):102-107.(LI Yu-chun,LOU Meng-lin,ZHOU Cheng.Analysis of Vertical Seismic Effects for Large-Scale Aqueduct Bridges[J].Journal of Earthquake Engineering and Engineer Vibration,2008,28(2):102-107.(in Chinese))
[6] AKKAS N,AKAY H U,YILMAZ C.Applicability of General Purpose Finite Element Programs in Solid-Fluid Interaction Problems[J].Computers&Structures,1979,10:773-783.
[7] 陈厚群,侯顺载,杨大伟.地震条件下拱坝库水相互作用的实验研究[J].水利学报,1989,7(7):29-39.(CHEN Hou-qun,HOU Shun-zai,YANG Da-wei.Study on Arch Dam-Reservoir Water Interaction Under Earthquake Condition[J].Journal of Hydraulic Engineering,1989,7(7):29-39.(in Chinese))
[8] WILSON E L,KHALVATI M.Finite Elements for Dynamic Analysis of Fluid-Solid Systems[J].International Journal of Numerical Methods in Engineering,1983,19:1657-1668.
[9] 高瑞强,宫必宁,郭建平.坝-水相互作用中水的压缩性影响研究[J].水利与建筑工程学报,2008,6(1):106-108.(GAO Rui-qiang,GONG Bi-ning,GUO Jianping.Study on Effects of Compressibility of Water in Dam-Water Interaction[J].Journal of Water Resources and Architectural Engineering,2008,6(1):106-108.(in Chinese))
[10]刘浩吾.混凝土坝动水压力与库水可压缩性效应[J].水利水电科技进展,2002,22(2):10-13.(LIU Haowu.Hydrodynamic Pressure on Concrete Dams and Reservoir Water Compressibility Effect[J].Advances in Science and Technology of Water Resources,2002,22(2):10-13.(in Chinese) )
Fluid-Solid Coupling Analysis of Dam-Reservoir Interaction
GONG Ya-qi,SU Hai-dong,CUI Jian-hua
(Yangtze River Scientific Research Institute,Wuhan 430010,China)
Dam-reservoir interaction was analyzed in this paper using fluid-solid coupling method.The reservoir water was modeled respectively by two types of finite element,namely pressure-based element and displacementbased element.The fluid-solid coupling method was compared with traditional Westergaard additional mass method and the comparison showed that the former was closer to the theoretical solution than the latter.The displacementbased element demanded more regular element shape than pressure-based element.Moreover,sensitivity analysis of selected areas of the reservoir showed that satisfactory results can be obtained if the length of reservoir area to be modeled was designed only 3-5 times the height of the dam.Finally,the compressibility of water was also explored taking the gravity dam structured model with different dam crest widths as an example.The present results will be helpful for the following research.
fluid-solid coupling;hydrodynamic pressure;natural frequency;compressibility
TV312
A
1001-5485(2011)06-0063-04
2010-05-24
长江科学院博士启动项目(CKSQ2010082)
龚亚琦(1980-),男,湖北武汉人,工程师,主要从事水工结构数值分析与计算工作,(电话)027-82829754(电子信箱)gong_yaqi@163.com。
(编辑:刘运飞)
