基于O-U过程具有不确定执行价格的期权保险精算定价

刘兆鹏，刘 钢

（宿州学院数学与统计学院，安徽 宿州 234000）

基于O-U过程具有不确定执行价格的期权保险精算定价

刘兆鹏，刘 钢

（宿州学院数学与统计学院，安徽 宿州 234000）

利用保险精算方法，给出股票价格遵循广义O-U（Ornstein-Uhlenback）过程模型具有不确定执行价格的欧式期权的精确定价公式以及买权和卖权之间的平价关系，进而推出有红利率的欧式看涨看跌期权的保险精算定价公式.

O-U过程；保险精算；期权定价；不确定执行价格

期权定价是现代金融数学的核心问题之一.1998年，Bladt和Rydberg[1]提出期权定价的保险精算方法，此方法不仅对无套利、均衡、完备的市场有效，且对有套利、非均衡、不完备的市场也有效.闫海峰等[2]用精算定价法得到了股价遵循O-U过程的欧式期权定价公式，赵巍等[3]讨论了在风险中性市场中股价遵循分数O-U过程的欧式期权定价模型，但这些模型均为对具有确定执行价格的期权进行定价，并不适用于具有不确定执行价格的未定权益的定价问题.

为了尽量降低风险，具有随机执行价格的新型期权会占据更广泛的市场.文献[4]首先研究了股价服从简单过程的具有不确定执行价的期权定价，文献[5]讨论了股价遵循O-U过程且具有不确定执行价格的欧式期权定价模型.在此假设股票遵循指数O-U过程，在无风险利率依赖于时间函数的情况下，利用保险精算定价方法，考虑了具有不确定执行价格的欧式期权定价问题，给出了精确定价公式以及买权和卖权之间的平价关系.

1 市场模型和保险精算方法

考虑一个连续时间金融市场，假定市场存在两种资产：一种是无风险资产，如债券；另一种是风险资产（或股票）.给定一个满足通常条件滤子流｛Ft｝t≥0的完备概率空间（Ω，F，（Ft）t≥0，P）.

股票价格过程S（t）遵循广义O-U过程

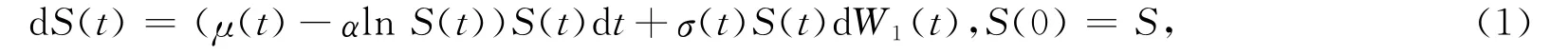
其中σ（t）为股票的波动率，μ（t）为股票的期望回报率，μ（t）和σ（t）充分光滑使得方程（1）有严格唯一正解，并且S＞0，α为常数.

假设K（t）为时刻t的执行价格，K（t）满足随机微分方程

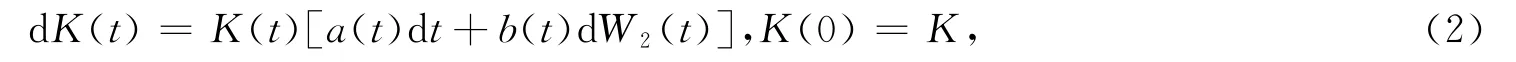
其中a（t），b（t）是时间的确定性函数，｛W1（t），0≤t≤T｝与｛W2（t），0≤t≤T｝是定义在（Ω，F，（Ft）t≥0，P）上的两标准Brown运动，其相关系数为ρ.

定义1 股票价格过程S（t）在[0，t]产生的期望收益率∫t0β（s）ds定义为

定义2 欧式期权的保险精算价值定义.当期权被执行时，股票到期日的折现值与执行价的折现值的差，在股票价格实际分布的概率测度下的数学期望值；其中无风险资产按无风险利率折现，风险资产按其期望收益率折现.欧式期权在到期日被执行的充要条件是：

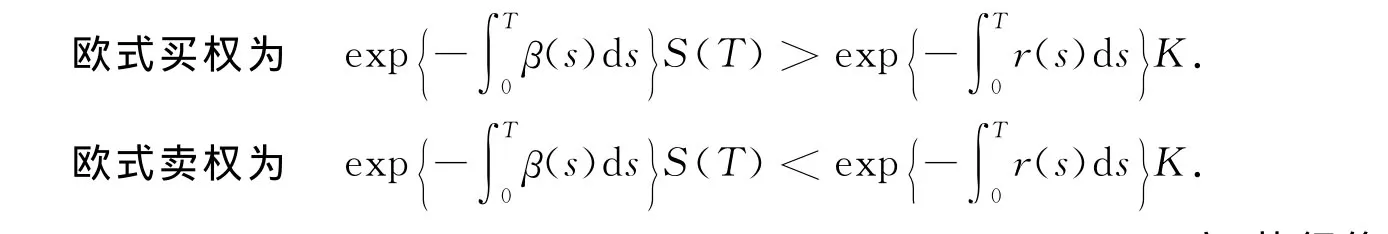
设C（K，T）和P（K，T）分别表示以股票价格S（t）为标的资产，执行价为K（t），到期日为T的欧式买权和卖权的保险精算定价.由上述定义得

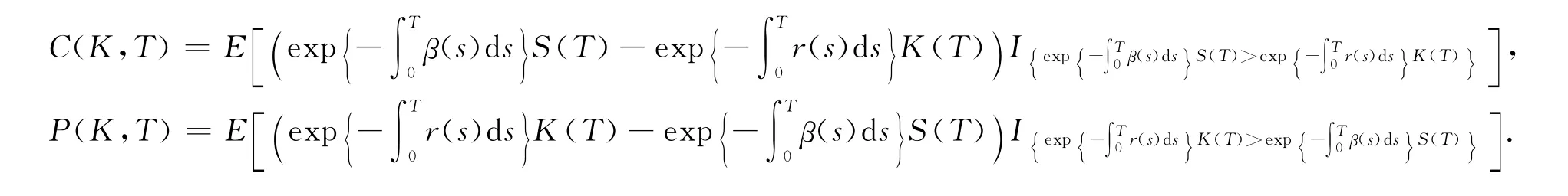
2 具有不确定执行价格的期权定价公式及推论

本节在市场模型假设（1）（2）下，给出了具有不确定执行价格的欧式看涨看跌期权的精算方法定价公式，并将结果推广到有红利支付的情形.

引理1 随机微分方程（1）（2）的解[6－7]分别为

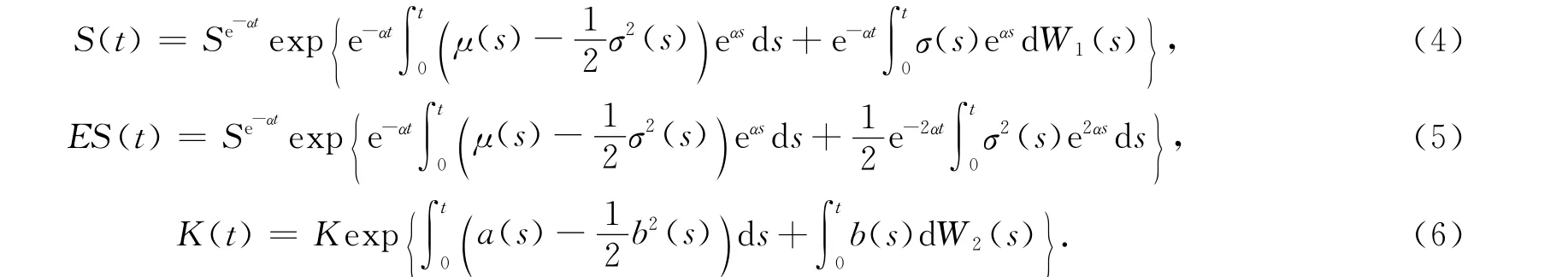
引理2 设两随机变量，W1～N（0，1），W2～N（0，1），Cov（W1，W2）＝ρ，则对任意的实数a，b，c，d，k，有下式成立：

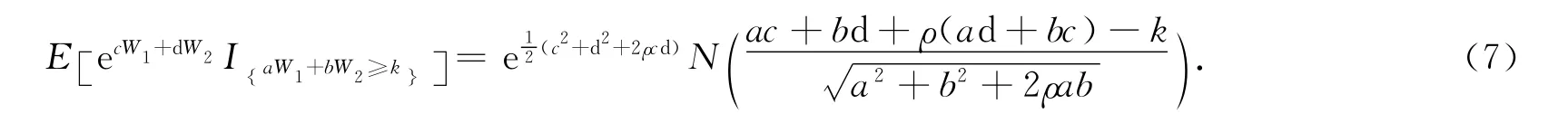
现分别考虑欧式看涨期权及欧式看跌期权，股票价格为S（t），执行价格为K（t），到期日为T.

定理1 设股票价格过程S（t）满足式（1），执行价格K（t）满足式（2），则欧式看涨期权与看跌期权t＝0的保险精算定价公式分别为

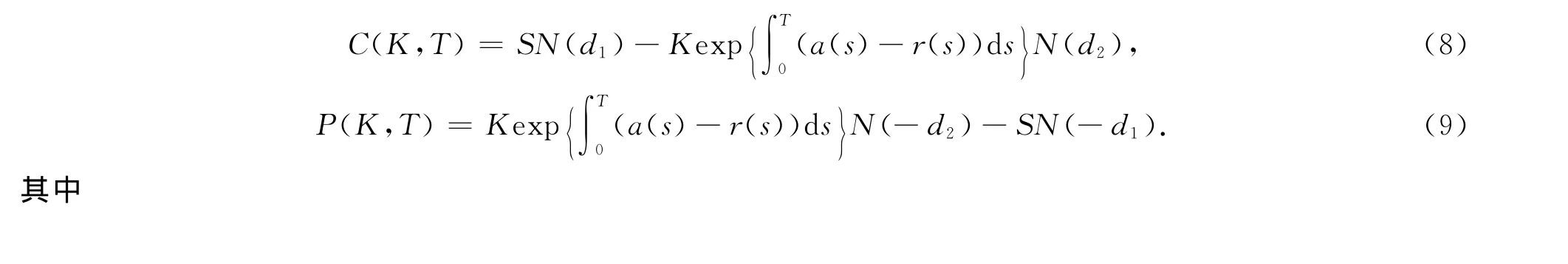
推论1 在市场模型（1）（2）下，保险精算定价方法的欧式看涨看跌期权的平价关系为

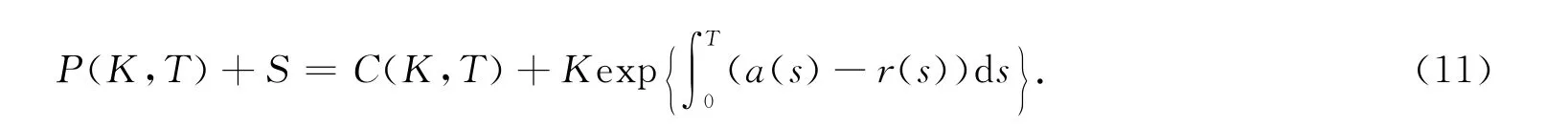
推论2 在市场模型（1）（2）下，考虑连续红利率q（t）的欧式看涨期权与看跌期权t＝0时刻的保险精算定价公式分别

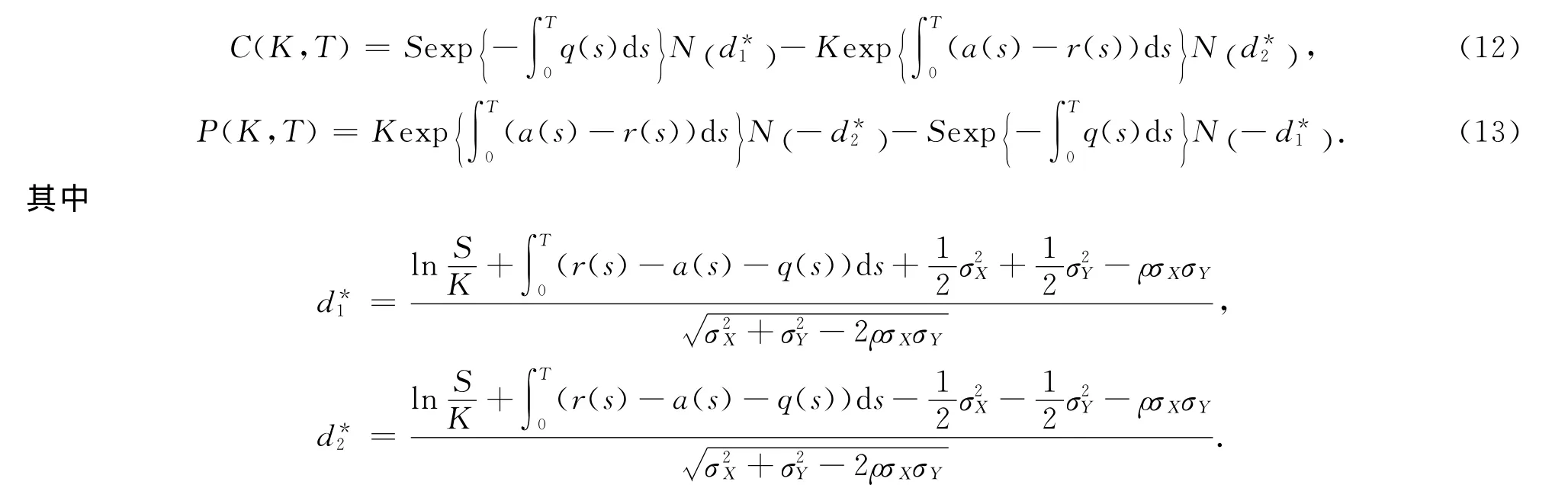
3 结束语

保险精算定价方法相对于传统的偏微分方程和鞅方法定价较为简单，且可得到精确的显式解.文章利用保险精算方法得到的结果克服了B-S模型对收益率假设的缺陷，使股票模型更加接近市场实际情况，同时对文献[2]的相关结果进行了推广和改进，给金融衍生产品创新提供了理论依据.

[1]Bladt M，Rydberg H T.An actuarial approach to option pricing under the physical measure and without market assumptions[J].Insurance：Mathematics and Economics，1998，22（1）：65-73.

[2]闫海峰，刘三阳.广义Black-Scholes模型期权定价新方法：保险精算方法[J].应用数学和力学，2003，24（7）：730-738.

[3]赵巍，何建敏.股票价格遵循分数 Ornstein-Uhlenback过程的期权定价模型[J].中国管理科学，2007，15（3）：1-5.

[4]薛红.具有不确定执行价格的期权定价模型[J].西安工程科技学院学报，2004，18（1）：87-90.

[5]郑晓阳，刘兆鹏.基于 O-U过程的具有不确定执行价格的期权定价[J].哈尔滨工程大学学报，2008，29（11）：1232-1235.

[6]陈琪琼.指数 Ornstein-Uhlenback过程模型下的期权定价[D].长沙：湖南师范大学，2005：2-6.

[7]刘坚，文凤华，马超群.欧式期权和交换期权在随机利率及O-U过程下的精算定价方法[J].系统工程理论与实践，2009，29（12）：118-124.

Actuarial Approach of Option Pricing with Change Exercise Price Based on Ornstein-Uhlenbeck Process

LIU Zhao-peng，LIU Gang
（School of Mathematics and Statistics，Suzhou College，Suzhou 234000，China）

Using the actuarial approach，the paper provided the accurate pricing formula and put-call parity of European option with change exercise price on the stocks whose price processes are driven by general Ornstein-Uhlenback process，and derivated the pricing formulas of European call option and the put option with continuous dividend yield.

O-U process；actuarial approach；option pricing；change exercise price

O211.6；F830.91 MSC2010：60H20

A

1674-232X（2011）04-0316-04

10.3969／j.issn.1674-232X.2011.04.006

2011-03-10

宿州学院自然科学研究项目（2009yzk20，2009yzk18）；宿州学院硕士科研启动基金（2008yss20）.

刘兆鹏（1981—），男，安徽宿州人，讲师，硕士，主要从事金融数学研究.E-mail：liuego＠163.com