奇异两点边值问题的四次样条解

尹丽蓉，余爱晖

（1.杭州师范大学钱江学院，浙江 杭州310012；2.浙江省淳安中学，浙江 淳安 311700）

奇异两点边值问题的四次样条解

尹丽蓉1，余爱晖2

（1.杭州师范大学钱江学院，浙江 杭州310012；2.浙江省淳安中学，浙江 淳安 311700）

用四次样条方法获得一类奇异两点边值问题的数值解.证明这种方法是一阶收敛的.最后用数值例子证明这种方法.

四次样条方法；函数；奇异两点边值问题；收敛阶；导数

1 介 绍

考虑如下一类奇异两点边值问题：

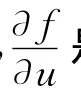
这样的问题产生于物理中的一些轴对称问题，文[1-3]用有限差分方法获得了奇异两点边值问题（1）的离散数值解.有限差分方法的精确度到目前为止最多只有二阶.Manoj Kumar[4]用二阶样条差分方法解决了问题（1）.A.S.V.Ravi Kanth等[5]用三次样条方法获得了奇异两点边值问题（1）的近似数值解.J.Rashidinia等[6]用带参数的三次样条方法获得了奇异两点边值问题（1）的近似数值解.

受文献[6]的启发，用四次样条方法获得的奇异两点边值问题（1）的近似数值解具有较好的精确度.最后用数值例子证明了这种方法的优越性.

2 四次样条方法

设S（x）是u（x）的四次样条近似解，把区间[a，b]用等区间结点

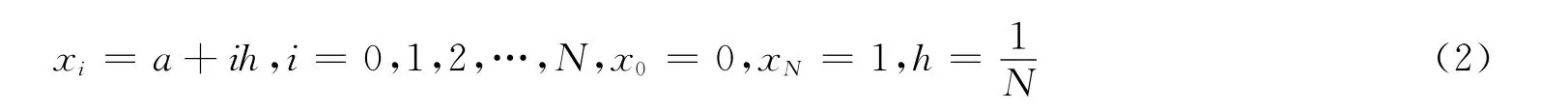
离散化，其中N 是正整数，函数S（x）∈C3[a，b]，四次样条函数S（x）在区间[xi，xi＋1]上通过满足如下形

式的Qi（x）表示出来：

首先用ui，ui＋1，mi，Mi，Mi＋1来描述上式中的5个系数.通过以下假设表示出来：

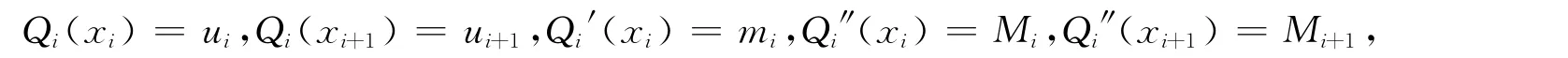
由此可以得到

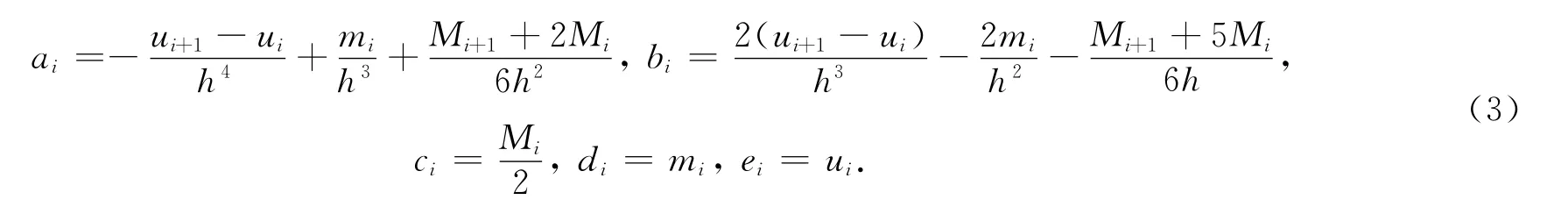
在区间[xi－1，xi]上，四次样条函数~Qi（x）的形式如下：

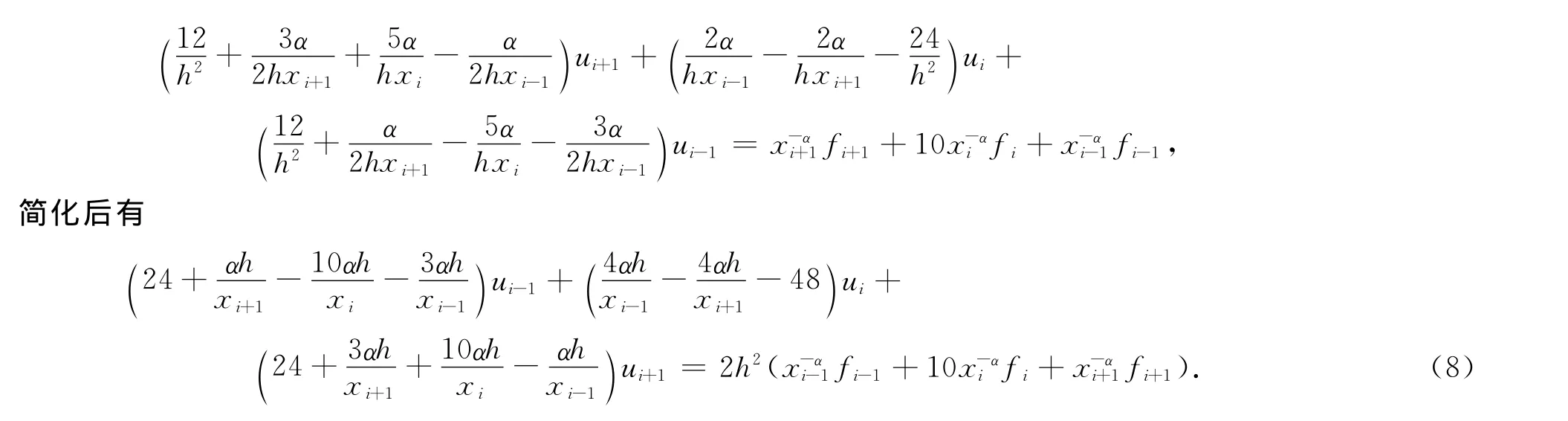
3 收敛性分析

上述方法可以写成如下矩阵形式：

4 数值例子

表1 例1的数值结果

表2 例2的数值结果

数值结果证明这种方法是稳健的且样条在区间点具有好的近似.

[1]Chawla M M，Katti C P.Finite difference methods and their convergence for a class of singular two-point boundary value problems[J].Numer Math，1982，39：341-350.

[2]Chawla M M，Katti C P.A uniform mesh finite difference methods for a class of singular two-point boundary value problems[J].SIAM J Numer Anal，1985，22：561-565.

[3]Chawla M M，ShivKumar P N.An efficient finite difference method for two-point boundary value problems[J].Neural Parallel Sci Comp，1996，4（3）：387-395.

[4]Manoj Kumar.A second order spline finite difference method for singular two-point boundary value problems[J].J Comput Appl Math，2003，142：283-290.

[5]Ravi Kanth A S V，Reddy Y N.Cubic spline for a class of singular two-point boundary value problems[J].J Comput Appl Math，2005，170：733-740.

[6]Rashidinia J，Mahmoodi Z，Ghasemi M.Parametric spline method for a class of singular two-point boundary value problems[J].Applied Mathematics and Computation，2007，188（1）：58-63.

Quartic Splines Solutions for a System of Singular Two-Point Boundary Value Problems

YIN Li-rong1，YU Ai-hui2
（1.Qianjiang College，Hangzhou Normal University，Hangzhou 310012，China；2.Chun'an High School Zhenjiang Province，Chun'an 311700，China）

This paper obtained the numerical solution for a system of two-point boundary value problems by quartic splines method，proved the present method is a fifth order convergent method，and demonstrated the method with some numerical evidence.

quartic splines method；function；singular two-point boundary value problems；the convergent order；derivable

O241.1 MSC2010：34B16；33F05

A

1674-232X（2011）04-0325-04

2011-01-11

尹丽蓉（1982—），山西忻州人，讲师，硕士，主要从事数论及其应用研究.E-mail：ylr2005＠163.com

10.3969／j.issn.1674-232X.2011.04.008