Aq-Analogof the Weideman's Formula

ZHENG De-yin，CHEN Guang

（College of Science，Hangzhou Normal University，Hangzhou 310036，China）

Aq-Analogof the Weideman's Formula

ZHENG De-yin，CHEN Guang

（College of Science，Hangzhou Normal University，Hangzhou 310036，China）

1 Introduction

Recently，Weideman's formula[1，Eq.（20）]called one of the hardest challenge identities：

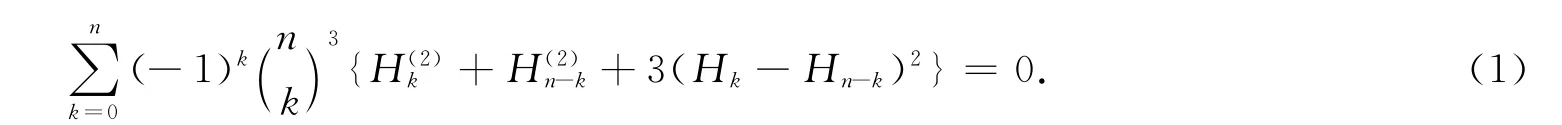
is closely concerned，where the harmonic numbers Hnand the second order harmonic number H（2）nare defined by

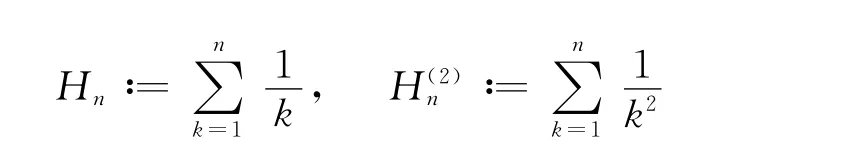
respectively.Schneider[2，Eq.（16）]（cf.[3，Eq.（12）]also）proved the formula（1）via computer algebra package Sigma，while Chu proved it using partial fraction method in[4，Eq.（6）]and hypergeometric series method in[5，Eq.（3）].The main purpose of this paper is to find q-analogs of Weideman's formula by means of partial fraction decomposition.

We use the standard notation on q-series.The q-shifted factorial（a；q）nis defined by

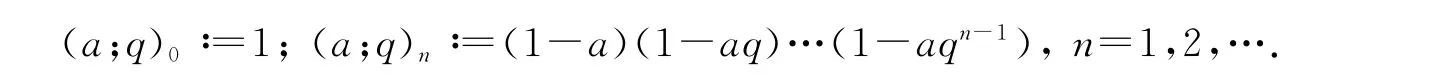
The q-binomial coefficient，or the Gauss coefficient，is given by

The paper investigated the decomposition of a class of rational function by partial fraction method，established a generalized identity about q-harmonic numbers，and obtained twelve striking q-like-Weideman formulas from twelve special cases of this general identity.

q-binomial coefficients；q-harmonic numbers；algebraic identities

With the above preparations，we can establish the following general q-algebraicidentity.

2 Partial fraction decompositions

Theorem 1 Let xbe an indeterminate and napositive integer.For any polynomial Q（x）of degree≤2＋3n，we have

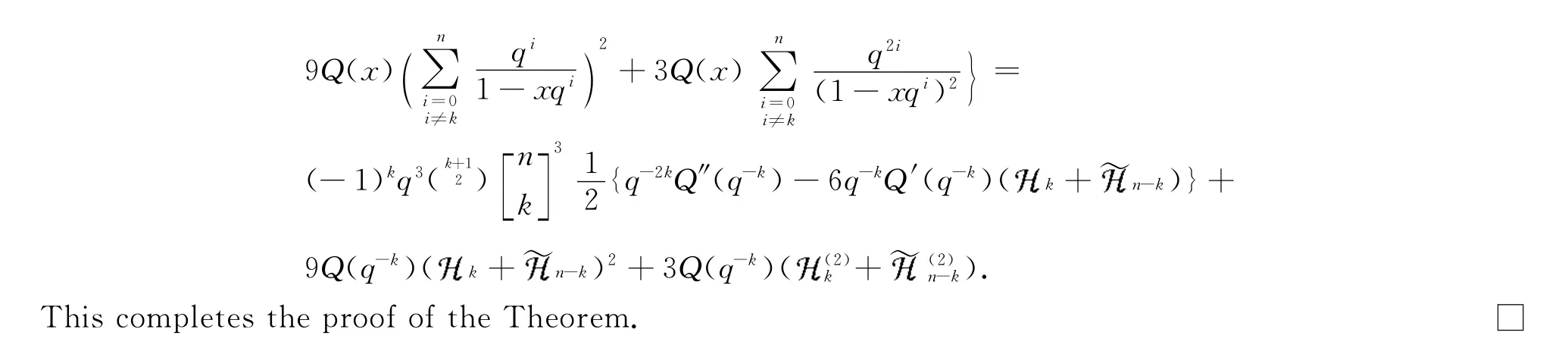
Multiplying by xacross equation（4）and then letting x→＋∞，we can obtain immediately the following general identity on q-binomial-harmonic number.

Theorem 2 Let n be a positive integer.For any polynomial Q（x）of degree≤1＋3n，there holds

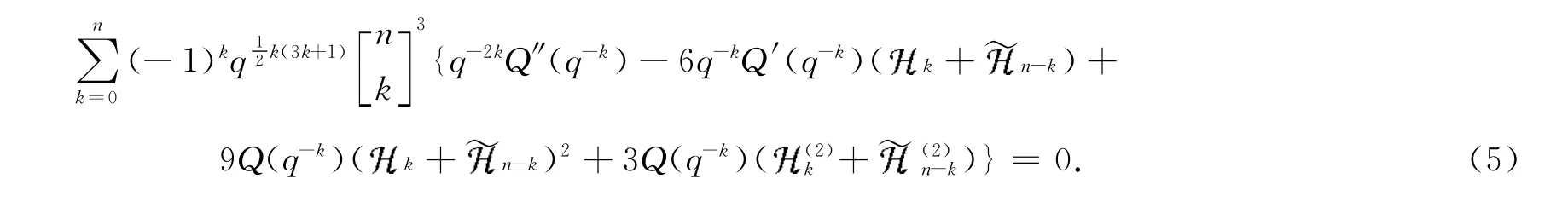
3 q-Harmonic number identities

Some interesting identities can be obtained by choosing different Q（x）in identity（5）.We will display some examples of this class of q-harmonic number identities in this section.

The list can be endless.However，we are not bothered to extend it further.The interested reader can do that for enjoyment.

[1]Weideman J A C.Padéapproximations to the logarithm I：derivation via differential equations[J].Quaestiones Mathematicae，2005，28（3）：375-390.

[2]Driver K，Prodinger H，Schneider C，et al.Padéapproximations to the logarithmⅡ：identities，recurrences，and symbolic computation[J].Ramanujan Journal，2006，11（2）：139-158.

[3]Driver K，Prodinger H，Schneider C，et al.Padéapproximations to the logarithm Ⅲ：alternative methods and additional results[J].Ramanujan Journal，2006，12（3）：299-314.

[4]Chu Wenchang.Partial-fraction decompositions and harmonic number identities[J].Journal of Combinatorial Mathematics and Combinatorial Computating，2007，60：139-153.

[5]Chu Wenchang，Fu Mei.Dougall-Dixon formula and harmonic number identities[J].Ramanujan Journal，2009，18（1）：11-31.

Weideman公式的一种q－模拟

郑德印，陈 广
（杭州师范大学理学院，浙江 杭州 310036）

使用部分分式方法将一类有理函数分解为部分分式，进而建立了一个一般化的q-harmonic数恒等式.作为例子，列出了此恒等式的12种特殊情况，得到了12个漂亮的类q-Weideman公式.

q－二项式系数；q-harmonic数；代数恒等式

date：2010-06-24

Supported by the Natural Science Foundation of Zhejiang Province of China（Y7080320）.

Biography：ZHENG De-yin（1964—），male，born in Tongbai，Henan Province，associate professor，engaged in combinatorics，hypergeometric series and special function.E-mail：deyinzheng＠yahoo.com.cn

O157.1 MSC2010：05A30；11B65Article character：A

1674-232X（2011）01-0011-04

10.3969／j.issn.1674-232X.2011.01.002