基于数组型并查集的连通域标记算法

罗志灶，周赢武，郑忠楷

（闽江学院物理与电子信息工程系，福建 福州350108）

基于数组型并查集的连通域标记算法

罗志灶，周赢武，郑忠楷

（闽江学院物理与电子信息工程系，福建 福州350108）

常用的二次扫描算法存在某些缺陷，即共同连通域的合并主要是通过重复遍历共同连通域标号数组，修改相应的共同连通域标号完成的．重复遍历严重影响算法的性能．数组型并查集算法利用树型数据结构特点实现连通域合并，以取代重复遍历．实验表明数组型并查集算法更具优势．

二值图像；连通域；像素扫描；标记

0 引 言

连通域标记是是介于图像预处理和目标识别之间的重要步骤．连通域标记是指将图像中符合某种连通规则［1］（4－邻域连通、8－邻域连通或m－邻域）的像素标识为同一目标［2］，并用唯一的标号标记连通域内的像素点［3］．通常图像的目标是由一个或多个连通域组成，因此，可根据连通域的属性，例如面积、二阶矩等，计算目标的特征值，以达到识别目标的目的．连通域标记是对扫描图像标记目标的过程，其运算量相当大．优化连通域标记算法可极大提高数字图像处理系统的性能．

影响连通域标记算法性能［3－4］的因素主要有：1）图像扫描的次数及连通域标号冲突处理的方法；2）内存访问的方法等．通常提高连通域标记算法性能的方法也是基于这两方面：减少图像的扫描次数，尽可能减少回溯扫描；合理设计内存访问方式，尽量减少连通域信息访问的时间．

连通域标记算法有多种类型［5］，根据扫描方式可分为像素扫描法［6］、线段扫描即线标记法［7］、基于轮廓的标记法［8］．像素点扫描方式有顺序扫描法［6］、递归标记法［9］、区域增长法［10］等．线段扫描算法主要是基于游程的标记算法［11］等．像素扫描法是最常用的标记算法，主要是遍历图像的像素点，并根据4－领域或8－领域规则，将相互连通的像素点用同一标号标记．基于游程的标记算法［11］是逐行扫描图像，并记录每行连通域的起始位置和终止位置，然后与下一行的游程比较，确定是否属于同一连通域．该算法占用内存少，适用于嵌入式系统．基于轮廓的标记算法［8］，是遍历图像的轮廓，并将在闭合的轮廓内的像素点标记为同一目标．该算法运算时间与图像的复杂度有关，因此应用不多．文献［5］分析了对连通域算法的进展及类别．

顺序扫描法是最常用的算法，其直观，数据结构简单，易于实现［6］．顺序扫描法有一次扫描法［9］、二次扫描法6和多次扫描法12．二次扫描法的性能及稳定性都比较好，是常用的算法．文献［6］分析了二次扫描法的原理及改进的方法．文献［3］提出等价标号快速传递法，并用决策树（decision tree）分析8－邻域和4－邻域内像素点的遍历秩序，以减少邻域内的像素点扫描次数；还提出用并查集（union－find）分析和处理冲突的等价连通域标号的思路，以提高等价标号冲突处理的效率．但文［3］中仅分析并查集算法原理，其算法实现不明晰，并且算法以过程调用方式植入连通域标记算法，严重影响连通域算法的性能．

在此首先针对二次扫描算法的缺陷提出改进的方法，分析和优化数组型并查集算法，特别对并查集的平面化算法优化，使算法易于实现，且充分利用数组直接访问存储的特点，提高算法的效率．最后，将本文的优化算法与文中提出的其它顺序扫描法相比较，分析优化算法的优缺点及适用范围．该文算法的4－邻域和8－邻域实现方法类似，将以4－邻域为例进行阐述．

1 二次扫描算法优化

1．1 常用二次扫描算法

描述算法之前先解释几个变量：BinaryImage（x，y）是二值图像某像素点（x，y）的灰度级，0表示背景，1表示目标．二维矩阵provisional（x，y）表示某像素点（x，y）的连通域标号，在算法的第一次扫描后，保存的是像素点（x，y）的临时连通域标号，二次扫描后，则保存的是目标的标号．一维矩阵common（index）表示由临时标号index标记的子连通域所属的共同连通域标号．例如，common（provisional（x，y））则表示由像素点（x，y）的临时标号provisional（x，y）所指定的共同连通域标号，是最终的、唯一的目标标号．二次扫描算法分为2个扫描阶段．

第一阶段，对二值图像BinaryImage进行扫描，按8－邻域或4－邻域规则，用临时标号provisional矩阵标记所有像素点．此时，会有大量的等价标号存在，即不同的临时标号标记的连通域属于同一目标的子连通域，将此类连通域标号称为等价标号．解决等价标号的方法是：用共同连通域数组common存储每个子连通域所属的共同连通域标号，共同连通域数组的下标表示子连通域的标号，其值则是目标的共同连通域的唯一标号．当遇到等价标号时，则重复扫描共同连通域数组，将等价标号的共同连通域标号改成一致．

第二阶段，扫描临时连通域标号矩阵provisional，对每个像素点的临时连通域标号用最终确定的、唯一的共同连通域标号替换，即实现连通域的合并．在连通域合并前，按共同连通域标号出现的次序，重新定序，确保目标连通域标号有效．合并后，标号矩阵中的像素点连通域标号即是最终所得的目标连通域标号．

在第一次扫描时，若在4－邻域内，若出现某像素点BinaryImage（x，y）＝1即属于目标像素点，且它的上邻域BinaryImage（x，y－1）＝＝1和左邻域BinaryImage（x－1，y）＝＝1即均属于目标像素点则；若它的上邻域共同连通域和左邻域的共同连通标号不一致，即common（provisional（x－1，y））≠common（provisional（x，y－1））时，则遍历整个common数组，将按如下处理冲突等价标号，实现连通域合并：

二次扫描算法中，若出现不一致的等价标号，则要遍历整个共同连通域common数组，实验表明，需花费大量运行时间重复遍历共同连通域数组．该文1．2节将介绍采用数组型并查集算法解决重复遍历共同连通域的问题，提高算法的性能．

1．2 数组型并查集（array of union－find）

并查集是一种树型的数据结构，常用于集合的分割和合并，解决判断两个子集是否同属一个集合，和把两个不属同一集合的两个子集进行合并的问题．并查集主要是利用树型结构存储和操作等价标号，并通过修改节点的左或上邻域实现连通域的合并．数组型并查集的特点是将其树节点以数组的形式保存，访问节点不是通过指针传递，而是通过检索数组．这可极大地缩小节点的访问时间．

如图1所示：树根节点的①⑧分别指向节点本身，表示是共同连通域；子节点②③指向根节点①；节点④⑤⑥⑦可通过父节点索引到根节点①．若树的根节点保存的是共同连通域的标号，则可在第一次扫描图像后，遍历所有的并查树，并将临时标号改为相应节点所指向的根节点的标号，实现连通域的合并．

数组型并查集同时拥有并查树和顺序存储的优点，适用于连通域标记算法．在二次扫描算法中，数组型并查集可用于解决连通域标号的访问和合并．在图像扫描过程中，若出现某目标像素点的左邻域和上邻域所指的共同连通域标号不一致时，可通过修改其左邻域或上邻域的共同连通域标号，完成共同连通域的合并；而不是如上节所示的遍历共同连通域数组．这样可节约大量的算法运行时间．

数组型并查集中的每个元素可表示某一子连通域，其下标是子连通域的临时标号，其值是该子连通域所处的共同连通域标号，如图2所示．由于扫描过程中的信息不充分，因此子连通域所指的共同连通域通常不是最终的连通域，仅是根据未完成扫描的信息所得的连通域，是临时的、不确定的．因此在算法扫描过程中经常出现某像素点的左邻域和上邻域的共同连通域不一致．

在图像扫描过程中，若出现某像素点和左、上邻域都是目标像素点，且左、上邻域的共同连通域标号不一致时，可利用数组型并查集实现它们的共同连通域合并．合并过程如下：

1）检索该像素点的左邻域和上邻域在并查集树的根节点．由于从叶节点到根节点的层次一般仅为2～3层，因此相对较快．

2）比较两子树的根节点的值，修改值较大的子树根节点，使其指向根节点值较小的子树的根．实验发现，在图像的扫描中，使较大根节点值的子树合并到根节点值较小的子树可有效地避免合并过程中形成网络的趋势．

当扫描某目标像素点时，其左邻域的连通关系如图1a，其上邻域连通关系如图1b所示．两个树分别表示某像素点的左邻和上邻域的连通域的逻辑关系．若其左邻域的共同连通域是②、上邻域的共同连通域是⑧，当扫描到该像素点时，判断出其左、上邻共同连通域标号不一致，则对其进行合并．合并结果如图3所示，合并仅修改较大根节点值的子树的根节点值．

图2表示合并前的某像点的左邻域和上邻域的连通关系，图4则是合并后的连通域关系，由图可知，合并仅是修改根节点值较大的子树的根节点的值，即将图中的⑧节点的值改为指向①．

1．3 数组型并查集（array of union－find）算法

通常数组型并查集算法旨在解决某目标像素点的左邻域和上邻域的共同连通域不一致时，连通域合并的问题．算法的复杂度体现在连通域的合并．在介绍算法前先假设一维并查集数组UF，初始化为0．该数组大小与临时标号的数量相同．临时连通域标号矩阵provisional，大小及维数与二值图像相同，用于保存每个像素点的连通域标号，在算法的第一阶段保存临时连通域标号，算法第二阶段保存像素点的最终目标标号．二值图像矩阵BinaryImage．

算法的第一阶段，扫描二值图像，用provisional保存像素点的连通域临时标号，对可能出现的情况按如下处理：

1）当遇到孤立新目标点时，添加临时标号，及新建树根节点．

2）当目标像素点与其左邻域或上邻域其中之一连通时，将其相邻邻域的临时连通域标号赋予目标像素点的临时标号．

3）当目标像素点与其左邻域及上邻域均连通，且左邻域和上邻域的共同连通域一致时，则仅需将其中一个邻域的临时连通域标号赋予目标像素点的临时标号．

4）当目标像素点与其左邻域及上邻域均连通，且左邻域和上邻域的共同连通域不一致时，则分别索引左邻域和上邻域的连通子树的根节点，比较根节点的值，将较大值的根节点指向较小值的根节点．

算法的第一阶段主要是完成临时连通域标记和并查树数组的建立，此时保存在并查树中的根节点是共同连通域标号，其它节点是临时连通域标号．共同连通域标号是断续的，且不是按扫描顺序排列的．因此需要第二阶段对其进行重新定序．

算法的第二阶段，主要是调整共同连通域标号，使之按扫描顺序出现，用共同连通域标号标记像素点的连通域标号．首先，遍历并查集数组UF，将所有的根节点（UF（i）＝＝i）按根节点出现的顺序重新编号，且取为负数；同时对非根节点检索其根节点，并将根节点值赋予非根节点．然后，将所有并查集数组的标号取为正数．最后遍历临时连通域矩阵provisional，用临时连通域所指的共同连通域标号替换临时连通域标号，完成连通域标记．标记后的目标连通域标号是顺序的、唯一的，按扫描中出现的次序标记目标．为后续处理带来极大的方便．

2 实验分析

选取复杂度不同的图像，并将本文算法（基于数组型并查集连通域标记算法）与改进前的二次扫描算法［6］、多次扫描算法［12］、改进型多次扫描算法［12］、基于游程算法［11］、基于链表算法［13］等进行比较．

选取不同结构的图像（512×512），在Matlab环境下，比较各算法的执行时间．链表型算法，采用模拟指针方法（Matlab不支持指针）．实验结果如表1所示．表1表示每幅图像（512×512）标记所用时间．多数情况下，二次扫描算法远优于其于算法，基于并查集的二次扫描算法是对二次扫描算法的优化，表2数据表明，基于并查集的二次扫描算法比二次扫描算法明显地减少了算法执行的时间．但任何算法均有其局限性，对于表1中的7．1．02．pgm图像，当目标过多且小时，基于并查集算法和二次扫描算法的反而不如多次扫描算法及改进型多次扫描算法．

算法的稳定性计算按如下方式进行：

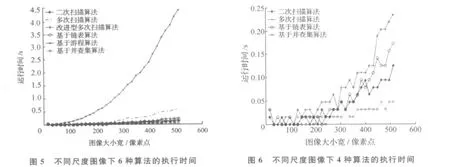
将512×512图像按16＊n×16＊n划分为32幅不同尺寸图像，以分析不同尺度图像的各算法的执行时间，并随机抽取其中一组数据，结果如图5、图6所示．图5将6种算法进行比较，图6则是将图5中相对执行时间较少的4种算法集中进行比较．由于Matlab计时不够精确，所以当执行时间很少时，会有图像更大时间反而更少的现象，但这不影响对算法执行时间的整体分析．图5、图6表明：在不同尺度图像下，基于并查集的二次扫描算法运行时间均少于其它算法，且随图像尺度的变化，基于并查集二次扫描算法呈线性变化，算法较稳定；与改进前的二次扫描算法相比，算法的平均运行时间减少约50%；从算法运行时间的一阶矩和二阶矩上看，稳定性也有相应的提高．

表1 不同图像特性及各算法性能

表2 二次扫描算法和基于并查集算法比较

3 结 论

利用并查集数组替代共同连通域数组，可减少处理等价标号冲突的时间．算法直观，易于代码实现．在优化二次扫描算法的基础上，提出基于并查集的二次扫描优化算法，利用并查集适用于分类与归并的特点，并结合二次扫描算法的优点．与改进前的二次扫描算法相比，该文提出的基于并查集的二次扫描算法的性能较其它连通域算法有很大的提高．参考文献：

［1］Gonzalez R C，Woods R E．Digital image processing［M］．2th ed．北京：电子工业出版社，2006．

［2］Sonka M，Hlavac V，Boyle R．Image processing，analysis and machine［M］．2th ed．北京：人民邮电出版社，2003．

［3］Wu K，Otoo E，Kenji S．Optimizing two－pass connected－component labeling algorithms［J］．Pattern Anal Applic，2009，12（2）：117－135．

［4］Luigi di Stefano，Bulgarelli A．A simple and efficient connected components labeling algorithm［C］／／10th International Conference on Image Analysis and Processing．Venice，Italy：IEEE Computer Society，1999：322－327．

［5］Costantino G，Borghesani D，Cucchiara R．Connected component labeling techniques on modern architectures［J］．Image Analysis and Processing，2009，5716：816－824．

［6］Samet H，Tamminen M．An improved approach to connected component labeling of images［C］／／Proc of CVPR．Washington DC：IEEE Computer Society，1986：312－318．

［7］章毓晋．图像工程（图像处理和分析）：上册［M］．北京：清华大学出版社，1999：205－206．

［8］Fu Chang，Chen ChunJen，Lu ChiJen．A component－labeling algorithm using contour tracing technique［J］．Computer Vision and Image Understanding，2003，93：206－220．

［9］徐正光，鲍东来，张利欣．基于递归的二值图像连通域像素标记算法［J］．计算机工程，2006，32（24）：186－225．

［10］Reddy B S，Chatterjib N．A FFT－based technique for translation rotation and scale invariant image registration［J］．IEEE Transactions on Image Processing，1996，5（8）：1266－1271．

［11］朱云芳，叶秀清，顾伟康．视频序列的全景图拼接技术［J］．中国图象图形学报，2006，11（8）：1150－1155．

［12］Kenji S，Horiba I，Sugie N．Linear－time connected－component labeling based on sequential local operations［J］．Computer Vision and Image Understanding，2003，89（1）：1－23．

［13］宋斌．一种新的图像连通域快速标号算法［J］．电子测量技术，2009，32（9）：67－73．

Abstract：The usual two－scans algorithms has some defects that common connected components are mainly merged via repeating to scan the label array of common connected components，and modifying relevant field of the array．The way seriously affects the performance of the algorithm．The algorithm based on array of union－find，which makes full use of the specialty of tree data structure to merge common connected components，can instead of the repeating scans．The experiments show that the algorithm based on array of union－find has more advantages than the algorithm which repeats to scan the label array of common connected components．

Key words：binary images；connected components；scanning by pixels；labeling

Labeling Connected Components Algorithm Based on Array of Union－Find

LUO Zhi－zao，ZHOU Ying－wu，ZHENG Zhong－kai
（Department of Physics ＆Electronic Information Engineering，Minjiang University，Fuzhou 350108，China）

TP391

A

1674－232X（2011）01－0086－06

10．3969／j．issn．1674－232X．2011．01．017

2010－09－08

福建省重点学科项目（闽教高［2006］48号）．

罗志灶（1971—），男，福建三明人，讲师，硕士，主要从事数字图像和嵌入式系统设计与开发研究．E－mail：lzz＠mju．edu．cn