一类具有无限长区间摄动方程的渐近解

陈 升，唐荣荣

（湖州师范学院理学院，浙江 湖州313000）

一类具有无限长区间摄动方程的渐近解

陈 升，唐荣荣＊

（湖州师范学院理学院，浙江 湖州313000）

利用匹配渐近展开法，讨论一类具有无限长区域的奇摄动问题．根据问题中参数p的变化，分3种情况对方程进行讨论．分别求得问题的外部解的内展开式（yo）i与内部解的外展开式（yi）o，利用匹配原理求出解的渐近展开式，得到这类问题的一般渐近解，丰富及推广已有文献中相应的结论．

无限长；非线性；摄动；渐近展开式；匹配

0 引 言

在众多领域中都存在着亟待解决的非线性问题，但在许多情形下非线性问题很难求得精确解，甚至不存在精确解．对于非线性问题，如果能够求得具有较高精度的近似解析解，无疑是十分有意义的工作．摄动方法是运用这种思想解决非线性问题的主要数学方法之一，它在工程、经济、航天、金融等领域都有着十分广泛的应用．国内外许多科学家，如Adelaida Vasil'eva、A．H．Nayfeh［1］、钱伟长、郭永怀、钱学森和林家翘等对摄动理论做了开创性的工作．近几十年来，许多数学工作者，如Bob O'Malley、林宗池、王莉婕［2］、唐荣荣［3－4］、韩祥临［5］等都致力于该方面研究．

匹配渐近展开法是求解非线性方程的诸多摄动方法之一，文献［1］用匹配渐进展开法讨论了一类二阶非线性奇摄动问题：

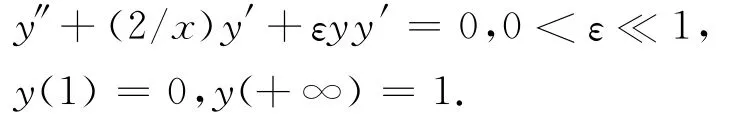
文献［5］讨论了如下类型的非线性奇摄动问题：

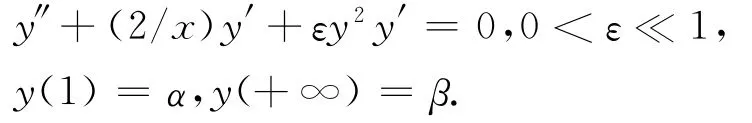
虽然文献［5］与文献［1］中的方程相比，只是y′的系数的非线性性更强一些，但笔者发现它们的解的表达式却有很大的不同．自然要问当y′系数的非线性性更加强烈时，其解是否存在，若存在，解的表达式又有什么性态．为了进一步了解这类方程更一般的情形，了解其解的性态，如下讨论更为广泛的二阶非线性奇摄动问题：

其中0＜ε≪1，p，n∈N＊，q∈R＋．

1 渐近展开式

1．1 解的外部表达式

令方程解的外展式为

将式（3）代入式（1）、（2），并令同次幂系数相等得

观察式（4）不难发现，两边同乘以x2，则式（4）变为欧拉型方程，则由常微分方程的相关知识及边界条件（5）可得

1．2 P＝1时

由于p＝1时，y0＝b1ln x．当x→＋∞时，ln x→＋∞不满足y（＋∞）＝1．所以y0在x→＋∞处失效，即当x→＋∞时方程的零阶外展开式非一致有效．为了求出一致有效展开式，引入收缩变换ξ＝xελ，

（9）其中λ是待定常数．

用ξ作为式（1）的自变量得到

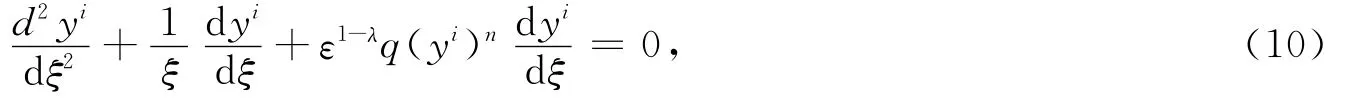
当ε→0时，由特异极限知λ＝1，式（10）变为

由边界条件y（＋∞）＝1，内部解可设为

其中ε→0时σ（ε）→0．

由于ξ＝xε，故ε→0时ξ→0，则可知

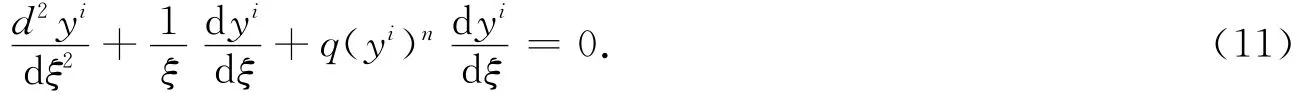
为了求得内展开式，由匹配原理可知

于是由式（12）、（14）可得

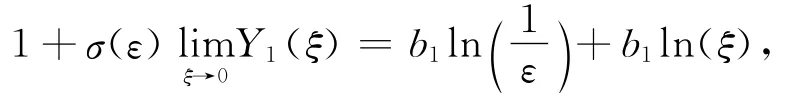
故有

将内部解（13）代入式（11）并令同次的σ（ε）的系数相等，则有

故由常微分方程的相关知识及边界条件Y1（＋∞）＝0得到

其中a0为常数．

为了匹配式（15）中的Y1，将Y1用ξ展开．又由于

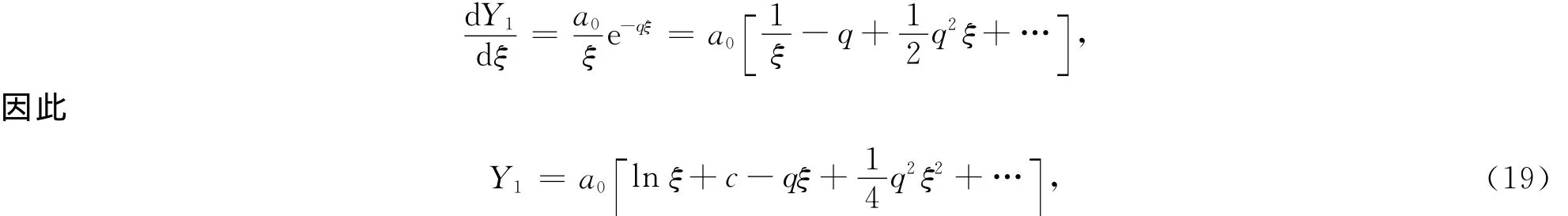
其中c为常数．故由式（17）、（18）可知

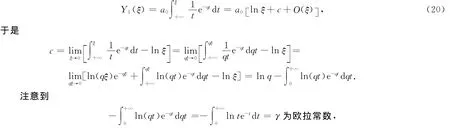
故c＝ln q＋γ，将c代入式（19）得到

则两项内展开式的外展开式为

观察式（15）与（21）容易发现式（21）中多出一常数，使得内部解与其外部解不能匹配．为了解决这个问题，需在外展开式中多展开一项与之匹配．

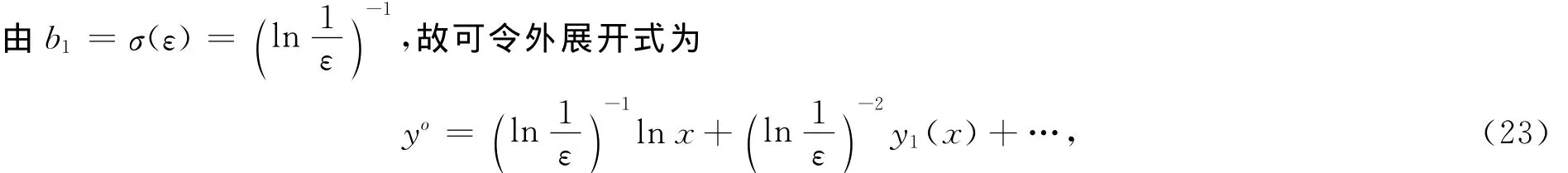
将式（23）代入式（1）和y（1）＝0得

由式（24）解得y1＝bln x，其中b为常数，于是两项外展开式的内展开式：

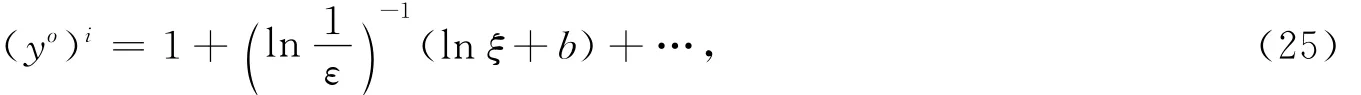
比较式（22）与（25），利用匹配原理可得a0＝1，b＝γ＋ln q．因此，

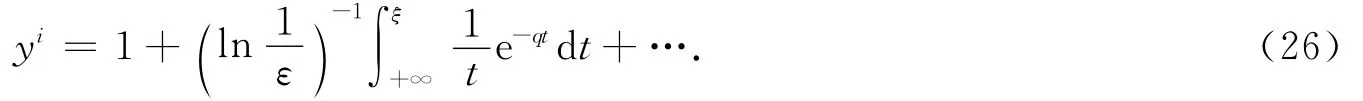
则得当p＝1时，方程的渐近解为

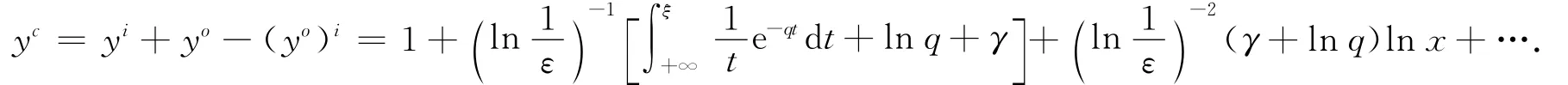
1．3 P＝2时

当x→＋∞时，由于y1→－qln x＋c2，它不满足边界条件y1（＋∞）＝0，由此讨论可知：问题外部解的渐近展开式在ε0阶一致有效，而在ε1阶上非一致有效．为了求出一致有效展开式，引入收缩变换

用ξ作为式（1）的自变量得知：当ε→0时，由相关知识知，特异极限对应于λ＝1，式（1）变为

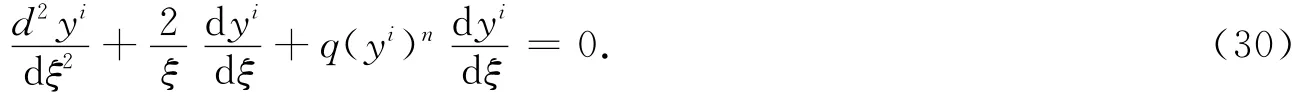
由边界条件y（＋∞）＝1，内部解可设为

将式（31）代入式（30），并令ε同次幂系数相等可得

由常微分方程相关知识解得

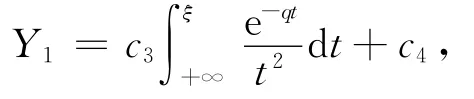
其中c3、c4为常数．又由边界条件y1（＋∞）＝0可知c4＝0．所以，内展开式为

两项内展开式的外展开式：

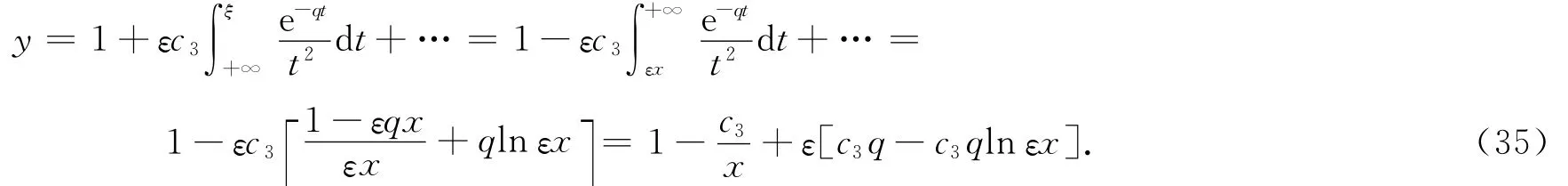
在式（34）中用x表示ξ，并令它与式（35）相等，可得c1＝q（n＋lnε－1）＋A，c3＝1．则当p＝2时，得方程的渐近解为

1．4 P≥3时

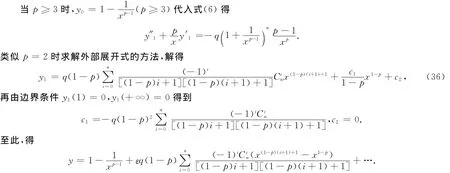
2 结 论

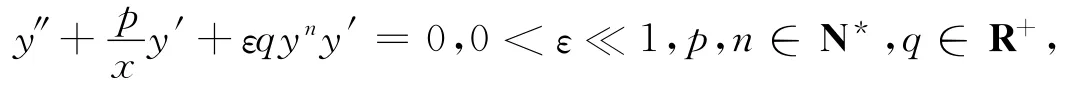
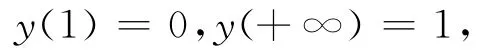
非线性方程：具有如下形式的渐近展开式：

从以上表达式可知解的表达式和性态会随着参数p的改变而改变．

当参数p取不同的值时，此非线性问题的外部解的一致有效性的阶数会随着参数p改变：当p＝1时，外展开式从零阶展开式开始就是非一致有效的；当p＝2时，外展开式的零阶展开式是一致有效的，非一致有效从一阶开始；进一步推想，此类含参数p的非线性方程的外展开式的渐近展开式非一致有效的阶数为p－1．事实证明p≥3时，方程渐近解的两项展开式都是一致有效的．本文用匹配法有效地解决了以上各种情况下解的非一致有效性．

［1］Nayfeh A H．Introduction to perturbation techniques［M］．New York：John Wiley ＆Sons，1981．

［2］王莉婕．一类非线性奇摄动问题的匹配解法［J］．大学数学，2005（8）：46－48．

［3］Tang Rongrong．The boundary layer problems for a class of fourth order nonlinear singularly perturbed equations［J］．J Math，2007，27（4）：385－390．

［4］Tang Rongrong．The shock problems for a class of nonlinear singularly perturbed equation［J］．数学进展，2005，34（2）：233－240．

［5］韩祥临．具有无限长区域非线性奇摄动方程［J］．安徽师范大学学报：自然科学版，2003，26（1）：1－4．

Abstract：Using the matching asymptotic expansion method，this paper discussed a class of singular perturbed problems with unbounded interval．According to the changes of the parameter pin the problems，the paper divided the discussion about the equation into three cases and obtained the interior expansion of outer solution （yo）iand the outer expansion of interior solution（yi）orespectively．Using the matching principle of asymptotic expansion，the paper also got the general asymptotic solutions for this kind of problems，which can richen and expand the corresponding conclusions．

Key words：unbounded interval；nonlinear；perturbation；asymptotic expansion；match

Asymptotic Solution for a Class of the Perturbation Equation with an Unbounded Interval

CHEN Sheng，TANG Rong－rong
（College of Science，Huzhou Teachers College，Huzhou 313000，China）

O175．14 MSC2010：34E15

A

1674－232X（2011）01－0042－06

10．3969／j．issn．1674－232X．2011．01．008

2010－05－11

国家特色专业“数学与应用数学”建设点；湖州市自然科学基金（2010YZ05）．

陈 升（1989—），男，浙江温州人，计算数学专业硕士研究生，主要从事微分方程研究．

＊通信作者：唐荣荣（1950—），女，浙江嘉兴人，教授，主要从事微分方程研究．E－mail：rrtang2005＠163．com