基于改进 RANSAC算法的图像拼接技术

黄 梅

(海南大学信息科学技术学院,海南海口 570228)

基于改进 RANSAC算法的图像拼接技术

黄 梅

(海南大学信息科学技术学院,海南海口 570228)

针对传统 RANSAC算法在图像拼接中效率低的问题,提出了一种解决该问题的新算法,即M_RANSAC算法.该方法首先通过 HARR IS算法提取 2幅图像中的特征点,且在特征点匹配排序的基础之上,根据数据错误率得出抽样次数,并采用双阈值法进行数据检验来提高算法效率.结果表明,M_RANSAC算法能有效地减少抽样时间和数据检验时间,同时降低了误矩阵的估算概率,提高了图像拼接的效率.

RANSAC算法;图像拼接;特征点匹配;抽样次数;数据检验

图像拼接是将数张有部分重叠的图像进行无缝拼接,生成一张宽视角、高分辨的全景图像.图像拼接技术关键在于图像配准和算法效率,目前针对不同类型的图像存在多种图像配准技术,其中基于特征点的拼接技术是现在最常用的拼接方法之一.在基于特征的拼接技术中,寻求特征点对应关系时需要计算变换矩阵,但实际上经过提取、匹配和去伪得到的匹配点远远大于计算变换矩阵所需的匹配点对.利用RANSAC(random sampling consensus)算法,可估算出变换矩阵,但当原始数据庞大、数据错误率高、估算模型复杂时,计算量会加大,效率会大幅度降低,针对这个问题,笔者提出了一种改进的 RANSAC算法,M_RANSAC算法,可以有效地解决效率降低问题.

1 RANSAC算法

RANSAC算法[1]是一种参数估算方法,其基本思想是针对不同问题,设计不同目标函数,在原始数据集中随机抽取M组抽样,每一组抽样的数据量根据目标函数而定.用M组抽样分别估算目标函数参数初始值,再计算每一组的参数初始值所对应的内点 (满足这一组参数初始值的数据点)和外点 (不满足这一组参数初始值的数据点).统计每一组参数初始值的内点数,内点数目越大,模型参数越好,最后根据一定的评选标准,找出最优目标函数的参数初始值.下面给出估算变换矩阵的 RANSAC算法步骤:

Step 1 根据 2幅图像存在的投影变换关系,确定一个变换函数,本文采用的是射影变换[2-4],它符合平面目标在不同视点、视角拍摄图像之间的变换关系,2幅图像对应特征点满足如下变换关系

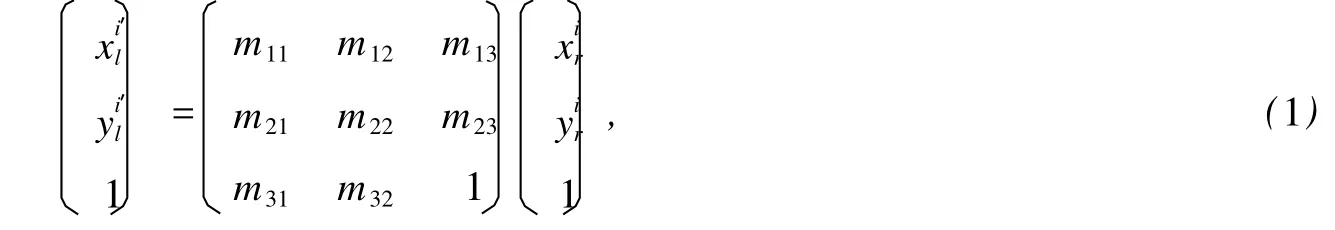
Step 2 从特征点对集合 S中随机反复的抽取一组数据,每一组抽样的样本数为估算模型所需最小数据量,计算该组抽样对应的模型,本文采用的模型参数需要 4对匹配点;

Step 3 用集合 S所有的数据来检验模型,即进行全数据检验,统计满足该模型的内点数量,以及内点变换点和内点匹配点的欧式距离之和,距离和公式如下

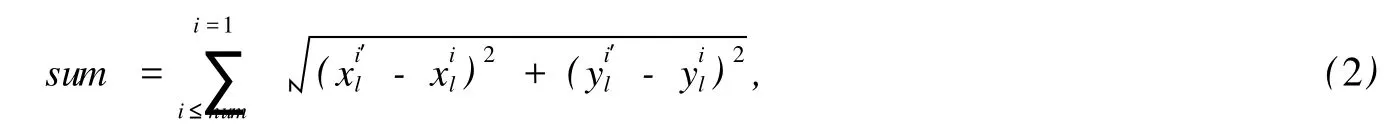
其中,num为满足模型的内点数量;

Step 4 根据内点数量和欧式距离和来选择模型参数;

Step 5 重复 Step2、3,直到选出满足评选标准的模型,找出这个模型对应的内点,并用这些内点计算出最终的模型参数.

RANSAC算法中,为保证在一定的置信概率P下,在M次抽样中至少有一组全是内点,这就要求抽样次数M足够大,利用式(3),可得置信概率P、数据错误率ε(外点在原始数据中所占的比例)、抽样数M和计算模型参数需要的最小数据量m之间的关系,即

从式(3)[5]可以得出,m,M,P和ε成指数关系,P不变时,M随ε,m的变大而变大,当抽样数M变大,就有更多模型进行全数据检验,所以当原始数据量庞大、模型复杂、数据错误率高时,直接造成 RANSAC算法效率下降.

以上分析可知,提高 RANSAC算法效率,可从减少抽样次数和减少模型数据检验时间方面来考虑.

2 M_RANSAC算法

2.1 抽样次数在 RANSAC算法中,从原始数据集随机反复抽取M组抽样,直到满足评选条件的模型被选出来,将原始数据集进行排序,从质量高的数据开始抽取,能更快地找到满足评选标准的模型,从而大大减少抽样次数.

对原始数据集中的数据排序,要回到特征点匹配,在匹配过程中,不可避免地存在一些错误匹配的特征点对,这不仅造成了原始数据集会存在一定错误率,而且也造成了模型估算不准确或抽样次数增加.在特征点匹配过程中,将匹配点对按一定顺序排序,使可信度高的匹配点对排在前面,即对原始数据集进行了排序,再从质量高的数据开始抽取,减少抽样次数.

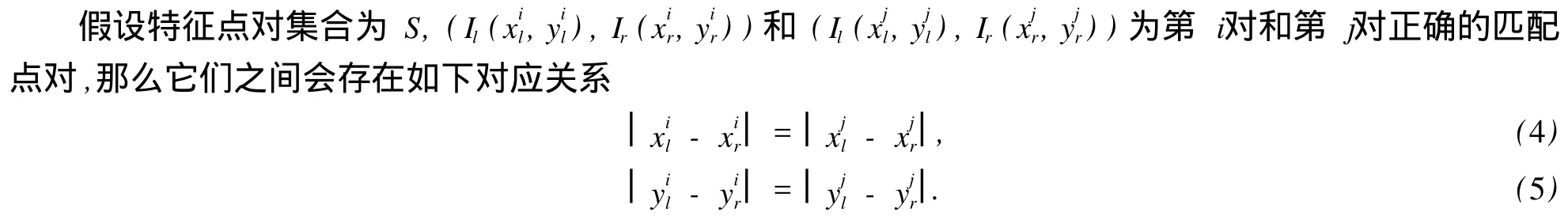
式(4)为第i对特征点对的行标的距离对值,等于第j对特征点对的行标的距离对值;式(5)为第i对特征点对的列标的距离对值,等于第j对特征点对的列标的距离对值.即对于任意两队正确的匹配特征点对来说,对应的坐标都应满足式(4)和(5),因此可认为,经过特征点匹配和去除伪特征点后,正确的特征点对在集合中是占大多数的.那么,根据特征点对的距离对值来对特征点进行排序.特征点对集合排序划分步骤如下

Step 1 求出所有特征点对的距离对值,行标的距离对值存在 distance_x矩阵中,列标的距离对值存在 distance_y矩阵中;

Step 2 统计所有特征点对的距离对值的种类,并统计每一种类的数量,记录属于这一种类的特征点对,例如(distace_xi,distace_yi)为第i对特征点对的距离对值,如果这个距离对值在已出现的距离对值种类中,没有与distace_xi,和distace_yi都相等的距离对值,则(distace_xi,distace_yi)为一种新的距离对值种类,如果在已出现的距离对值种类中,存在与distace_xi,和distace_yi都相等的距离对值,则在原有距离对值种类中数量加 1,并将记录第i对特征点属于这个种类的距离对值.

Step 3 按照种类数量多少进行排序,假设得到的距离对值种类为n,那么就对特征点对集合S划分为n个集合S1,S2,S3,…,Sn,第 1个集为数量最多的距离对值种类所对应的特征点对集合S1,第 2个集合为数量第二多的种类所对应的特征点对集合S2,以此类推.

排序后,将S1,S2,S3,…,Sn这n个集合重新划分为m个新集合{S1},{S1,S2},{S1,S2,S3},…,{S1,S2,S3,…,Sn},并对这m个新划分的集合设定m个递增的数据错误率,{S1}的数据错误率最低,以此类推.根据式(3),可计算出不同错误率下的最大抽样次数.假设{S1}的抽样次数为M1,如果在M1次抽样次数中没有得到满足评选条件的模型参数,则将抽取范围扩到集合{S1,S2},抽样次数为M2,以此类推,直到出现满足评选条件的模型参数.

2.2 数据检验时间在 RANSAC算法中,每一次迭代计算的变换矩阵模型都进行了全数据检验,即数据集中的所有点都参与了模型检验.如果减少参与全数据检验的模型便可减少数据检验时间.根据上文将征点对集合S的划分,可以在每次产生新的模型参数时,首先在进行本次抽样的质量高的数据集合中进行检验,假设为{S1,S2},如果这个模型的内点比例超过了预先设置一个集合内点比例B1(内点数与取样集合例如{S1,S2}中数据点数的比值)和集合欧式距离阈值T1,则这个模型可以参与全数据检验,否则丢弃这个模型,进入下次抽样.在原始数据庞大的情况下,可大大减少模型数据检验时间.

2.3 M_RANSAC算法的实现本文采取 HARR IS算法[6]提取不同尺度下的特征点[7-9],双向归一化方法[10-11]匹配特征点,循环阈值和比较特征点距离对值的方法[11]去除伪匹配点,得到特征点对集合S.

M_RANSAC算法步骤如下:

Step 1 将特征点对集合S按照距离对值种类的多少对特征点进行排序划分,划分为n个集合S1,S2,S3,…,Sn.

Step 2 将S1,S2,S3,…,Sn这n个集合重新划分为m个新集合{S1},{S1,S2},{S1,S2,S3},…,{S1,S2,S3,…,Sn},设定m个递增的数据错误率,根据式(3)计算出不同错误率下每个集合的最大抽样次数Mmax_i.

Step 3 从第i个集合中随机抽取(i从 1开始,即从{S1}开始抽样)4对匹配点,根据每组的抽样数据,计算模型参数,集合抽样数记为Mi,集合每迭代一次Mi加 1,当集合抽样数Mi大于第i个集合的最大抽样次数Mmax_i时,i=i+1转下个集合中开始抽样,如果Mi≤Mmax_i则转到 Step 4.

Step 4 计算模型参数在第i个集合中的内点比例和内点的欧式距离和,设定集合的内点比例阈值为B1,集合的欧式距离和阈值为T1,如果内点比例大于B1,并且内点的欧式距离和小于T1,则转到 Step 5,否则回到 Step 3,重新开始抽样.

Step 5 对模型参数进行全数据检验,设定全数据的内点比例阈值为B2,全数据的欧式距离和阈值为T2,如果模型内点比例大于B2,并且欧式距离和小于T2,则转到 Step 6,如果不满足,回到 Step 3,重新开始抽样.

Step 6 利用选出的模型参数,计算模型所有内点,从而计算出最终的模型.

M_RANSAC算法在特征点排序划分的基础上,计算出不同错误率下最小抽样次数减少了抽样时间,并采用了预检测法将参与全数据检验的模型减少,节省了大量数据检验时间.

3 实验结果

验证改进后的算法效果,用 4幅图像进行 2组实验,图像如图 1a,图 1b,图 2a,图 2b.实验条件:CPU Intel core i3 2.27 GHz、内存 2 G、操作系统W indows 7、Matlab7.1.实验数据来源:图 1a和图 1b来源于网络,分辨率为 525×350,图 2a和图 2b来源于云台拍摄,分辨率为 533×400.

图1 风景画面

图2 海南大学教学楼

从图 1a和 b可知,2幅图关系简单,求出模型也为简单的平移模型.在模型相对简单,原始数据较少时,从表 1可知算法效率上没有太大区别

表1 风景画算法结果分析表

实验求出的模型为

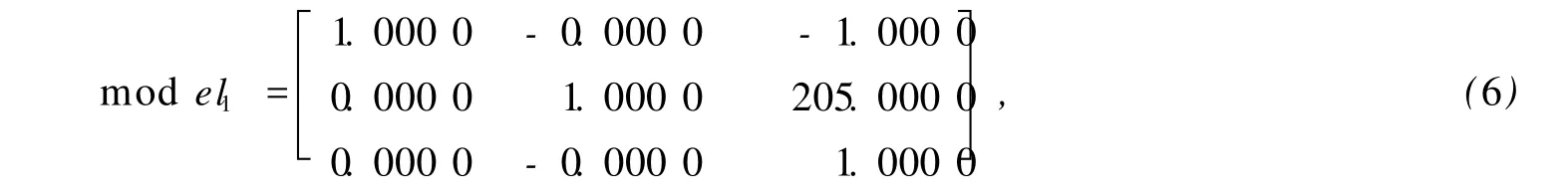
将图 1a和图 1b拼接成为图 3.

图3 风景画拼接结果图

图2a和图 2b这 2幅图像,存在平移、旋转、仿射的关系,提取特征点相对多,求出的模型也相对复杂,从表 2中可知,在这种情况下,改进后的算法比传统算法效率高.

表2 海南大学教学楼算法结果分析表

求出的模型为

将图 2a和 b拼接成为图 4.

图4 海南大学教学楼拼接结果图

从(11)式知,当情况变复杂,即原始数据庞大(SN变大),数据错误率高(M变大),模型复杂时(一个数据检验一个模型需要的平均时间为t3会变大),算法的时间差会变大,从而导致 RANSAC算法效率大幅度降低.图 5为采用了M_RANSAC算法拼接的全景图.

图5 海南大学教学楼全景图

4 结 论

本文提出的一种高效的M_RANSAC算法,能快速地寻找模型参数.当原始数庞大、数据错误率高、模型复杂时,M_RANSAC算法比传统 RANSAC算法稳定,且能快速估算出模型参数,其效率更高、更有效地提高了全景图的拼接效率.

[1]MART IN A I,ROBERT C B.Random Samlpe Concesus:proceeding ofA Paradigm forModel Fittingwith Applications to Image Analysis and Automated Cartography[J].Communications of the ACM,1981,24(6):381-395.

[2]R I CHARD Z,HEUNG-YEUNG S.Creating FullView Panoramic ImageMosaics and EnvironmentMaps:the 24th annual conference on Computer graphics and interactive techniques,LosAngeles,August,3-8,1997[C].New York:ACM press/Addision-wesley publishing co,1997.

[3]曹红杏,柳稼航.基于角点变换矩阵的图像拼接[J].计算机应用,2008,8(16):4536-4529.

[4]YAO Li,MA L I-zhuang.A Fast and Robust Image Stitching Algorithm:proceeding of the 6th World Congress on Intelligent Control and Automation,Dalian,Jun,21-23,2006[C].Dalian:[s.n.],2006.

[5]WEILi-fang,HUANGLin-lin,PAN Lin,et al.The Retinal ImageMosaicBased on Invariant Feature and Hierachical TransformationModels:proceeding of the 2nd International Congress on Image and Signal Processing,Tianjin,October 17-19,2009[C].Tianjin:[s.n.],2009.

[6]HARR IS C,STEPHENSM.A combined corner and edge detector:proceeding of the 4th Alvey vision conference,Manchester,August,31-Septemter,2,1988[C].Manchester:[s.n.],1998.

[7]程邦胜,唐孝威.Harris尺度不变性关键点检测子的研究[J].浙江大学学报:工学版,2009,43(5):855-859.

[8]LOWED G.Disctinctive Image Features For m Scale-Invariant Keypoints[J].InternationalJournalof ComputerVison,2004,60(2):91-110.

[9]M IKOLAJCZYK K,SCHM ID C.Scale&Affine Invariant Interest PointDetectors[J].International Journal of ComputerVistion,2004,60(1):63-86

[10]ZITOVA B,FLUSSER J. Image registration methods:a survey[J]. Image and Vision Computing,2003,21(11):977-1000.

[11]仵建宁,郭宝龙,冯宗哲.一种基于兴趣点匹配的图像拼接方法[J].计算机应用,2006,26(3):610-612.

I mageMosaicMethod Based on I mproved RANSAC

HUANGMei

(College of Infor mation Science and Technology,Hainan University,Haikou 570228,China)

Because of the disadvantages of the low efficiency of traditional RANSAC algorithm in image mosaic,a new algorithm,M_RANSAC algorithm,was proposed.Firstly,the feature points were extracted by HARR IS algorithm,then based on the sorting of thematching pairof feature points,the timesof random selectionwere obtained by the error rate of data and the data testingwere implemented by themethod of double threshold.The results indicated that this new algorithm,M_RANSAC algorithm,can efficiently decrease the time of the random selection and the date testing,reduce the likelihood of false matrix assessing at the same time,which can be applied in image mosaic successfully.

RANSAC algorithm;image mosaic;feature pointsmatching;sampling frequency;data testing

TP 391.41 < class="emphasis_bold">文献标志码:A

A

1004-1729(2011)02-0172-06

2011-02-21

黄梅 (1987-),女,江西赣州人,海南大学信息科学技术学院 2008级硕士研究生.