计算机模拟技术在逆向云发生器中的应用

李 丹， 董春游

(黑龙江科技学院 计算机与信息工程学院，哈尔滨 150027)

计算机模拟技术在逆向云发生器中的应用

李 丹， 董春游

(黑龙江科技学院 计算机与信息工程学院，哈尔滨 150027)

针对采集大量的定量信息存在一定的困难，引入了计算机模拟技术。利用计算机模拟技术，可以由采集到的少量的云滴信息模拟出大量的云滴信息。逆向云发生器可以实现定量数值到定性语言值的转换，其精度依赖于定量数值的数目，误差随着定量信息的增加而减少。通过实例验证，结果表明:模拟数据可信，该研究为提高逆向云发生器算法的精度提供了一种新的方法。

逆向云发生器;计算机模拟;云模型

0 引言

云模型是李德毅在传统模糊集理论和概率统计的基础上，建立的一种定性定量不确定性转换模型。它把不确定性概念的模糊性和随机性有机地结合在一起，实现了不确定语言值与定量数值之间的自然转换［1］。正向云发生器和逆向云发生器是云模型中两个最基本、最关键的算法，前者实现了语言值表达的定性信息中获得定量数据的范围和分布规律，这是一个前向的、直接的过程;后者是将一定数量的精确数值有效转换为恰当的定性语言值［2］，是个逆向的、间接的过程。在这个过程中，不可避免的会有误差存在。实验证明，云滴数越多，所得到的特征值的误差就越小，云滴数n＞10时，可以比较准确地得到Ex(误差小于0.01)，当云滴数n＞100，En的相对误差小于1%，而对He，当n＞200时，相对误差小于10%［3］。为了减少逆向云发生器的误差，需要采集大量的定量信息，而对于许多评价问题，如多属性评价或综合评判，收集大量的评价数据又存在困难。如某一待评价对象，如果它不是大众所了解熟识的，而是某一领域需要有专业知识的人才能对其进行正确的评价，这就需要听取该领域专家的意见，为了保证算法的精确度，需要请大量的专家分别对其进行评价。如上所述，为了保证He的误差小于10%，一方面，需要请至少200个专家，另一方面，即使请到了这么多专家又如何能保证他们同时到场。为了解决上述问题，引入了计算机模拟技术。其基本思想是根据多个专家给出的评价信息进行统计分析，模拟出所需数目的专家评定模拟值，为科学评价奠定基础。

1 计算机模拟的步骤

计算机模拟主要包括数据的采集与整理、模拟模型的构造、模拟程序的编制和验证、模拟运行、结果分析等步骤，其流程如图1所示。

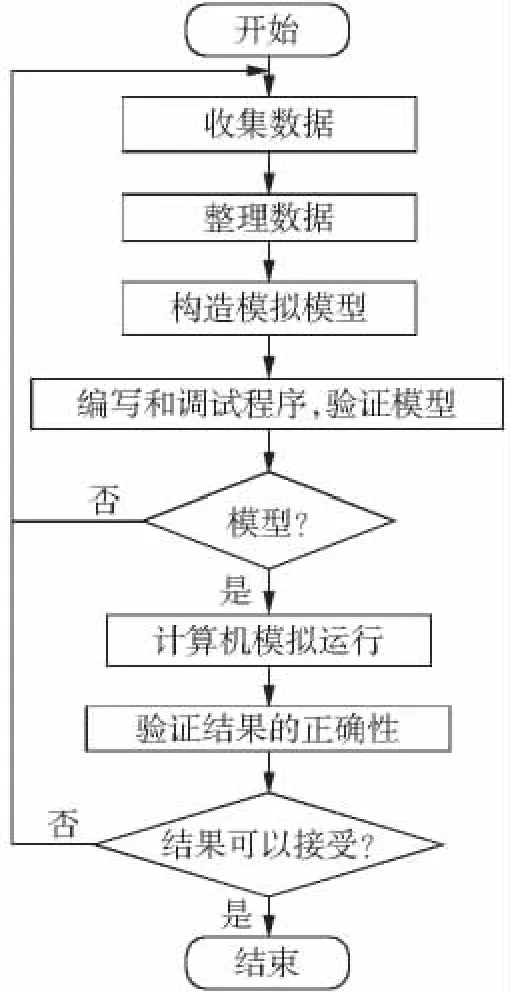
图1 计算机模拟流程Fig.1 Flowchart of computer simulation

1.1 收集数据及整理

收集若干个原始的评价数据。数据整理指根据收集到的数据推断数据总体的分布。一般地，从收集到的数据来推断总体X的分布分为两步:一是根据数据值大致地了解总体的可能分布;二是进行分布函数的拟合检验。

1.1.1 概率密度的近似求法——直方图法

频度分布和直方图在辨识一个分布的形状时是很有用的。直方图可以按照下列步骤构造:

(1)找出数据中的最小值和最大值，分别记为a和b，数据个数记为n。

(2)将区间［a，b］分为m个子区间(m的值与n有关，一般近似等于样本大小的平方根，且应使每个子区间至少包含一个样本观测值)，每组组距(子区间长度)为(b－a)/m。

(3)记ni(i=1，2，…，m)为样本观测值落在第i个子区间(ai－1，ai］的个数，称为频数，fi=ni/n是样本观测值落在区间(ai－1，ai］中的频率。在xOy平面上，对每个i(1≤i≤m)，以区间(ai－1，ai］为底，yi= fi/(ai－ai－1)为高，作一排直的长方形，即为直方图。

由文献［4］可知，当n充分大时，直方图的外廓曲线近似于总体X的概率密度曲线。因此，利用直方图法，可以大致地描述总体X的概率密度的概貌。

1.1.2 分布函数的拟合优良度检验

设总体的分布函数F(x)为未知，(X1，…，Xn)为总体X的样本，欲根据样本检验假设

其中F0(x)是某个已知的分布函数。对上述假设H0作显著性检验，称之为分布函数的拟合检验。分布函数的拟合检验方法很多，最主要的是χ2检验法，其步骤是:

(1)将总体X的全体可能值分成m个互不相交的区间(ai－1，ai］，i=1，2，…，m，计算样本(X1，…，Xn)的观测值出现在第i个小区间(ai－1，ai］的频数ni和频率ni/n，ni和ni/n分别称为经验频数和经验频率。

(2)求出当H0成立时，总体X取值于第i个小区间(ai－1，ai］的概率:

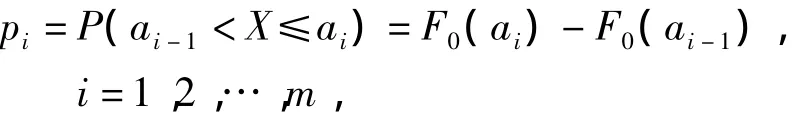
称npi为理论频数，pi为理论频率。

选皮尔逊统计量:

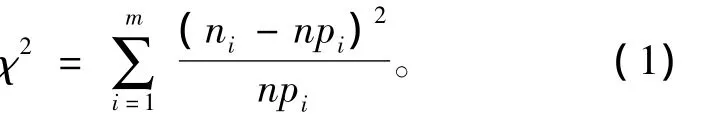
费希尔推广了皮尔逊定理，证明了式(1)渐近服从χ2(m－r－1)分布，其中m为小区间数，r为待估参数的个数。因而，对给定的显著性水平α，由χ2分布表可得临界值(m－r－1)，使得P(χ2＞(mr－1))=α，于是得拒绝域((m－r－1)，∞)。

(3)作出判断。由样本观测值计算统计量χ2的观测值。若χ2＞(m－r－1)，则拒绝H0;反之，接受H0。

1.2 模拟模型的建立

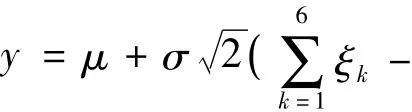
1.3 模拟程序的编制和验证

运用计算机程序语言将系统的数学逻辑模型转变为主要由计算机程序组成的模型，以便在计算机上进行模拟运行。进行调试性模拟以验证数学逻辑模型是否正确反映现实系统的本质，以及模拟模型是否正确实现数学逻辑模型，从而修改模型和调整计算机程序。

1.4 结果分析

当产生计算机模拟数据以后，要对计算机模拟输出数据值与实际值进行假设检验，样本均值和样本方差常被用来估计假设分布的参数。所以通常采用t检验法和F检验法［5］来验证真实值与模拟值之间是否有显著性差异。

1.4.1 t检验法

检验两正态总体样本均值差的假设用t检验法。

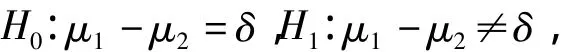
这里δ是已知常数，当δ=0时，就是检验两个正态总体的均值是否相等。

取检验统计量为

1.4.2 F检验法

检验两正态总体样本方差比的假设用F检验法。

2 计算机模拟技术在逆向云发生器中的应用

以问卷调查的形式收集20位专家对某一待评价对象的定量评价信息，通过对调查表的回收、整理和统计，得到定量评价信息如表1所示。

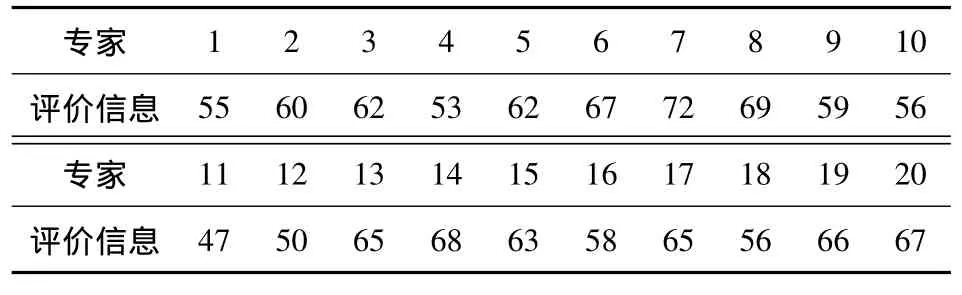
表1 定量评价信息Table 1 Quantitative data

运用上述计算机模拟的步骤，采用Java语言进行编程实现，最终得到200个模拟评价数据。模拟得出的评价信息与专家给出的评价信息非常接近。利用t检验法和F检验法对两组数据进行假设检验后，得出两组数据的平均值和方差无显著性差异，所以模拟出的数据是可信的。

根据采集到的评价信息和模拟出的评价信息，利用无须确定度信息的逆向云发生器算法即可得到云模型的数字特征。

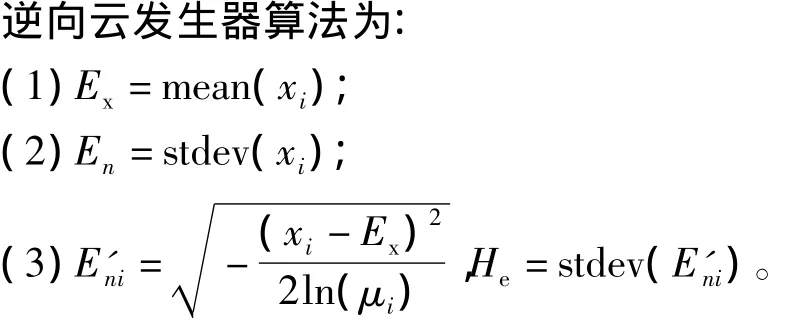
其中，mean()，stdev()分别为求均值和标准差的函数。

3 结束语

逆向云算法可以用于从定量知识得出定性评价。但为了保证算法的精确度要求有较大数量的云滴数，而很多时候采集大量的原始数据又存在一定的困难，为了解决上述问题，将计算机模拟技术引入到逆向云发生器中，它是众多专家集体智慧的结晶，与传统的一个或几个专家的评价信息相比较，其结果具有更高的准确性，更具科学性、合理性，为得出对象的正确评价结果奠定了基础。计算机模拟技术与逆向云的结合，不仅可以用于多属性评价或综合评判中求参数Ex、En、He，还可用于不确定性推理中求云滴的确定度μ(x)以及云发生器的确定点μ、a等。

［1］邓 羽，刘盛和，张文婷，等.广义多维云模型及在空间聚类中的应用［J］.地理学报，2009，64(12):1439－1447.

［2］罗自强，张光卫.一种新的逆向云算法［J］.计算机科学与探索，2007，1(2):234－240.

［3］吕辉军，王 晔，李德毅，等.逆向云在定性评价中的应用［J］.计算机学报，2003，26(8):1009－1014.

［4］刘次华，万建平.概率论与数理统计［M］.2版.北京:高等教育出版社，2003.

［5］刘卫江.概率论与数理统计［M］.北京:清华大学出版社，2008.

Application of computer simulation technology in backward cloud generator

LI Dan， DONG Chunyou
(College of Computer＆Information Engineering，Heilongjiang Institute of Science＆Technology，Harbin 150027，China)

Aimed at addressing a more difficult collection of an increasing number of cloud droplets，this paper introduces computer simulation technology which makes possible the simulation of a large number of cloud droplets by the collected value.Backward cloud generator(BCG)capable of transforming quantitative values into qualitative concepts exhibits an accuracy determined by the number of quantitative information and the decreasing deviation of BCG due to the increasing number of quantitative information.The experiment shows that the simulation data are reliable.The study provides a new method designed for improving the accuracy of BCG.

backward cloud generator;computer simulation;cloud model

TP18

A

1671－0118(2011)04－0329－04

2011－07－11

李 丹(1982－)，女，黑龙江省鸡西人，讲师，硕士，研究方向:人工智能、决策支持系统，E-mail:fdpld@126.com。

(编辑徐 岩)