非线性弹簧阻尼减振装置的探究

罗 尧 王 慧

（1电子科技大学电子工程学院，四川 成都 610000）

（2电子科技大学物理电子学院，四川 成都 610000）

非线性弹簧阻尼减振装置的探究

罗 尧1王 慧2

（1电子科技大学电子工程学院，四川 成都 610000）

（2电子科技大学物理电子学院，四川 成都 610000）

将汽车底盘减振装置简化为以非线性弹簧、阻尼器为主的被动阻尼式吸振器.利用Matlab软件对其在简谐力作用下的响应进行定量绘图分析，研究其振幅衰减、缓冲周期以及与由线性弹簧构成的简单模型进行比较，解释了减振装置具体的工作过程以及其中的基本工作原理.

弹簧振子；被动式阻尼器；非线性振动；共振；Matlab

1 引言

振动的一种主要工程应用即是基于弹簧阻尼减振的车辆底盘减振系统的设计［2］.减振系统是衡量一辆汽车性能优劣的重要参数.在相关研究与教学中，为了简便起见，大部分的案例模型往往简化为线性弹簧振子与阻尼器的并联系统［8］.然而在实际生活与工程应用中，车辆的颠簸振动常常超出线性模型的适用范围，继而产生非线性振动［5，6］.为了更好地研究减振装置在非线性区域的振动状况，本文将在线性减振系统基础上，将非线性弹簧阻尼系统引入.经过物理建模，理论推导以及仿真分析［1，10］，得出更为符合实际情况的车辆减振模型，为实际工业工程生产提供更有参考价值的参数.

2 非线性渐硬弹簧的振动特性

最为典型的振动模型是线性弹簧振子.对于线性弹簧振子，其振动方式由如下微分动力学方程惟一确定

k称为弹簧振子的劲度系数，只由弹簧本身特性决定.弹簧振子的线性振动仅发生在振幅较小的情况下.随着振幅增加，或是弹簧质量的分布不均，弹簧的振动将趋于非线性行为.其一种典型的振动方式由如下微分动力学方程确定

在实际应用中，上式多简化为如下形式

当k2＝0且k3＞0时恢复力比线性关系所预期的值大，称为非线性渐硬弹簧.实际生活与工程应用中，更多的振动都以此为基本物理模型发生在非线性区域内.对于由式（3）确定的单自由度振动系统，当忽略阻力，对其回复力

进行积分：

式中，W 为势能改变量.解得

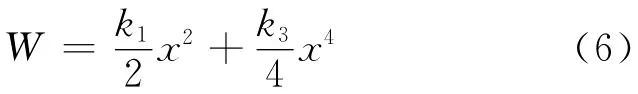
分别取k1＝1，k2＝0.005，利用 Matlab绘出其势能变化曲线如图1所示.

图1 势能曲线

其曲线依然关于x＝0对称.其势能曲线比线性弹簧略陡，表明随振幅增大其响应大于线性弹簧响应，振动速度更快，频率更高.设m＝1，k1＝1，x0＝0，0＝1，k3＝0或k3＝0.5，绘出其振动曲线如图2所示.

图2 振动曲线

由图2可得，非线性弹簧振动周期小于线性弹簧振子，振动速度大于线性弹簧振子.

3 弹簧阻尼吸振器的激励响应

现在我们考虑由非线性弹簧振子与被动式阻尼所组成的被动阻尼式吸振器，研究其在受到简谐激励下的系统响应.对其受力以及振幅衰减特征进行分析与研究.

对于零输入响应下的有阻尼非线性振动系统，其运动可由如下微分方程表征

其中，c称为系统的阻尼系数.

对于一辆行驶在近似平坦路面上的车辆，其遇到的颠簸可近似的由一周期性变化力F进行表征，可设为F＝F0cos ω t，则上式可以改写成为如下形式

在存在阻尼的线性振动系统中，强迫振动位移和强迫力之间有一个相位差，我们可以预先确定强迫力的相位，继而确定解的相位.但对于非线性阻尼系统，计算显然更为复杂.一种较为简单的办法是：固定解的相位，然后求强迫力的相位.即认为解x（t）和强迫力间的相位差是不变的，并选取解的相位为零，而强迫力的相位待定.此时式（8）可取如下形式

设

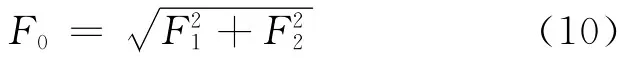
其中，F1、F2、F0、c皆为k3的同阶小量.其中F1，F2为周期变化力F的振幅F0正交分解后的分量，其比值为所设相位差.假设x（t）的近似解为

比较两边三角函数的系数并进行整理可得

在该方程中，b表示行驶车辆的颠簸频率，ω表示路面起伏的频率，F0表示路面起伏的最大作用力，A表示车辆在整个颠簸过程中的最大振幅.

分析可得，对于周期性激励作用下的车辆行驶颠簸，振动的振幅随着频率的增加而增加.而频率又与车辆行驶时的速度存在线性相关关系，当频率达到时振幅达到最大值，即此时车辆的振动最为明显.对于非线性振动的一个有趣现象是，若研究方程（13）绘成的图像便可以发现，当振动频率衰减并接近某一临界值时振幅会产生突然增加或突然减少的现象.此现象就是非线性阻尼振动在简谐激励下的跳跃现象.

从数学上考虑，振幅达到最大值时所对应的跳跃点之间的振幅曲线是不稳定的，所以跳跃现象的理解在数学上变成了周期解的稳定性分析，在实际生活中也可以从车辆船舶主轴的振动等现象中观测到这种跳跃现象.

现在分析其在某一确定的但不是跳跃点所对应的频率下的衰减振动，即给定无激励作用下的达芬方程一个初始条件：x（t＝0）＝x0＝1（t＝0）＝0＝1.取m＝1000kg，k1＝1000.对于c以及k，我们给出如下三组数据观察其相应情况的变化.（1）c＝k3＝500；（2）c＝k3＝1000；（3）c＝k3＝2000.利用Matlab的微分方程解算程序解微分方程组，并绘出方程的x（t）—t图以及v（t）—x（t）相图如图3、4所示。

图3 位移时间x（t）—t图

图4 速度位移v—x相图

分析图像我们可以得出，当取所示初始条件时，弹簧在给定一个初始瞬时激励的作用下的振动将根据c以及k3的变化而变化.随着这两个数值的增加，系统振动结束的时间将缩短，当c以及k3超过某一临界值时，系统将不再做振动而直接达到平衡位置，用时也最短.在工程应用中，一部分减振装置就采用达到临界值的阻尼系统，以期得到最短响应时间使系统振动迅速衰减.

4 线性与非线性吸振器的对比

通过以上研究以及在参考文献中对于线性被动式阻尼吸振器的研究分析，我们可以总结出这两种减振装置在工作原理与实际应用效果中的几点差异.

首先，线性系统的微分方程式存在确定的解析解，这使得求解整个系统在任意时刻的振动情况变为可能.而对于非线性系统而言，大部分方程需使用诸如迭代法等近似解法或者是计算机软件诸如Matlab对其进行数值分析以求得近似解.同时，在线性系统的振动响应中，解的形式往往可以表示成暂态响应与稳态响应的叠加之和.然而在非线性系统中，由于叠加定理不再适用，所以必须在考虑模型具体情况之后确定相应的近似解法.虽然准确性不能达到线性系统的精度，但是其精度已经能够很好地满足实际工程需要，且更符合工程应用中的实际情况.

其次，有阻尼非线性振动的应用前景广泛，不仅出现在本文叙及的车辆减振应用中，在无线电技术和光学等其他领域也有着广泛的实际应用.它的诸如振幅在频率改变时的跳跃现象等特性在车辆遭遇颠簸时的受力分析等过程中是不可忽视的影响因素，通过对这些线性系统所没有的特性的研究，可得到更为优化的解决方案.

最后须指出的是，以上针对非线性阻尼吸振的特性探讨都建立在F1、F2、F0、c皆为k3的同阶小量的情况之下.当这个条件不再成立时，系统振动的模式将趋于分频模式甚至将产生混沌现象.这些现在作为混沌力学的理论研究范围已经成为了一个重要研究分支.

5 结论

本文通过引入对于非线性弹簧振子，改进和优化了线性被动式阻尼吸振器的物理模型.在借助Matlab软件的数值分析所得出的结果的基础上，探讨了非振动被动式阻尼吸振器的振幅特性，衰减特性，频率改变时振幅的跳跃特性以及其在实际工程中所对应的具体的物理意义.

通过这些探讨我们发现了非线性系统对于几种典型激励不同于线性系统的种种特性，发现了振动过程中存在微扰以及浑沌运动的可能性，为车辆底盘以及传动主轴的减振吸振装置的设计提供了一些新的思路和参数的参考，也以实例印证了计算机模拟及数值分析在现代物理学以及工程应用中的重要作用.

［1］ 谢善娟.用Matlab分析非线性弹簧振子的振动 ［J］.赤峰学院学报，2009，（4）：7～8

［2］ 龙岩，史文库，李辉 等.被动吸振器在整车振动控制中的应用 ［J］.噪声与振动控制，2008，（10）：105～108

［3］ 倪亚贤，董慎行.对称非线性弹簧振子的周期特性 ［J］.大学物理，2003，（4）：22～24

［4］ 石新军，朱旭宁.弹簧振子非线性振动的幅频特性 ［J］.宝鸡文理学院学报（自然科学版），2004，（6）：147～149

［5］ SINGIRESU S R.Mechanical Vibrations ［M］.Beijing：Tsinghua University Press，2009

［6］ 王海期.非线性振动 ［M］.北京：高等教育出版社，1992

［7］ 马涛.数字化大学物理 ［M］.杭州：浙江大学出版社，2008

［8］ 闻邦椿，李以农，张义民 等.振动利用工程 ［M］.北京：科学出版社，2005

［9］ 药树栋，宫建.平弹簧振子振动的探讨 ［J］.大学物理，2008，（2）：22～24

［10］ Edward B M.An Engineer’s Guide to MATLAB ［M］.Publishing House of Electronics Industry，2006

STUDY OF THE NONLINEAR DAMPING SPRING SHOCK ABSORBERS

Luo Yao1Wang Hui2
（1School of Electronic Engineering，University of Electronic Science and Technology of China，Chengdu，Sichuan 610000）
（2School of Physics and Electronics，University of Electronic Science and Technology of China，Chengdu，Sichuan 610000）

This article simplified the shock absorbers system of cars as a passive damping absorber model which mainly consisted of nonlinear spring and damper.We quantitatively plotted and analyzed the response of our model under a simple harmonic force with the Matlab software to study its amplitude attenuation and cushioning period.We made a comparison between our model and the model of linear spring shock absorbers to explain the technological processes and basic work theorem of the whole damping system.

spring；passive damping aperture；nonlinear vibration；resonance；Matlab

2010－09－26；

2011－01－05）