地球化学异常下限的含量-面积分形计算方法——以江西永平地区为例

胡青华, 肖晓林, 曹圣华, 吴明仁, 冯国圣, 熊 伟

(江西省地质调查研究院,江西南昌 330030)

地球化学异常下限的含量-面积分形计算方法
——以江西永平地区为例

胡青华, 肖晓林, 曹圣华, 吴明仁, 冯国圣, 熊 伟

(江西省地质调查研究院,江西南昌 330030)

地球化学元素的异常下限值确定是地球化学中重要的问题之一,传统的方法只考虑了数据的随机性,对自相似性和不规则性数据则有所欠缺。采用含量-面积法来确定地球化学元素的异常下限,其结果和传统计算方法对比表明,该方法具有更好的理论基础和实用性,能有效的提高地球化学异常的识别精度。

分形;异常下限;地球化学;含量-面积法

地球化学异常一直是进行矿产预测的重要依据,地球化学下限是圈定地球化学异常的重要工作之一,迄今为止还没有找到一个合理计算地球化学异常下限的科学方法。传统的地球化学异常下限的确定主要是使用经典的统计学方法,以样品数据呈正态分布为假设前提,通过计算数据的统计学参数对异常下限进行确定,一般是以平均值与 n倍的标准离差之和作为地球化学异常下限值,即:

其中 T为异常下限值,X为平均值,S0为标准离差,n=1～3。

该方法仅适用于地球化学数据呈正态分布或对数正态分布的情况,但新的研究表明元素的地球化学分布并不局限于正态分布或对数正态分布(李长江,1999;谢淑云等,2003;Allegre et al.,1995;Turcotte.,1986),非正态分布或对数非正态分布的元素数据具有不规则性和自相似性,李长江等(1995)研究揭示的地球化学景观可能是一个具有低维(D=2.9)吸引的混沌系统,具有典型的分形特征,因此可以作为分形来处理。

1 分形模型原理及算法

分形分布的特点要求大于等于某一尺度的数目或数,与物体大小之间存在幂函数关系,即

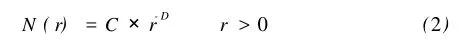
其中 r表示特征尺度,C>0称为比例常数,D>0称为分维数,N(r)表示尺度大于等于 r的数目。例如,r表示某元素的含量,N(r)表示元素含量大于等于r所围成的面积。

为了求分形模型中的分维数 D,将观测数据(N(r1),N(r2),N(r3),…,N(rn))和 (r1,r2,r3,…,rn)绘在双对数坐标纸上,如果其散点大致分布在一条直线上,分维数 D可以直接利用直线的斜率,即将观测数据 (N(r1),N(r2),N(r3),…,N(rn))和(r1,r2,r3,…,rn)代入 (2)式,然后两边取常用对数,(2)式化为线性回归模型:

用最小二乘法求出斜率D的估计量,即分维数;如果其散点大致分布在两段直线上时,可以采用分段拟合,有的分界点清楚,有的测不清楚,为了提高分界点确定的客观性,在两个区间用最小二乘法进行回归时用最优化方法确定分界点。其基本思想是,找出合适的分界点 roī,使各区间拟合的直线与原始数据之间的剩余平方和 Ei(i=1,2)在两个区间的总和,即

为最小。其中 ri0是分界点;D1和D2分别为相应的斜优选法,即分维数。为了检验回归方程的显著性,应对每个回归方程进行相关系数及方差分析检验。分界点的的意义就在于元素含量在空间上至少存在两个层次的分布,rio对应的值为地球化学元素的异常下限值。

2 永平地区水系沉积物地球化学元素异常下限的求解

GIS技术具有强大的海量数据处理能力和空间信息处理能力,中国地调局一直致力于Mapgis及其二次开发软件的应用,如MemapGis(数字地质调查系统),通过MapGis和分形理论的结合,将有效提高计算地球化学异常下限的可信度和效率。本文采用永平地区 1∶5万水系沉积物 Zn元素做为例子,用含量-面积法确定元素的异常下限,其实现流程如简图1。

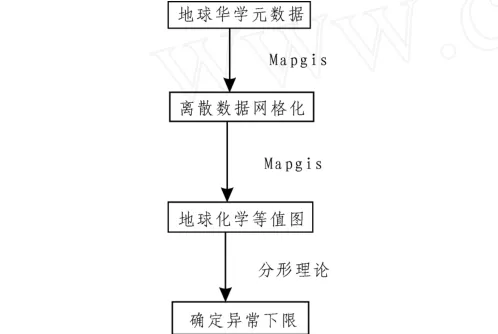
图1 地球化学异常下限的确定方法流程图Fig.1 The flow chart ofmethod for threshold of element geochem ical anom alies

2.1 传统的统计法计算异常下限

永平地区共取得水系沉积物样品共 9 244个,对原始数据进行特高值处理后用异常下限公式计算 Zn元素异常下限为 158.2×w(B)(10-6)。

2.2 含量面积法计算异常下限

用MapGis的DT M分析模块,将 Zn元素含量数据进行网格化,再进行平面等值线图的绘制,生成一个包含起始值、终止值和面积的区文件 (图2),通过MapGis空间分析系统或MapGis属性库管理,将区文件中的起始值、终止值和面积值导出,利用含量-面积法进行分形计算统计 Zn元素 (N=9 224)(表 1)。

表 1 空间分析系统求出 Zn元素数据的N(r)Tab.1 The N(r)of Zn data calculated by spatial analysis

应用表 1中的数据通过 EXCEL实现分形统计(表 2)。通过表 2知道,符合公式 (4)的数据分组位置为表 2中第 11个分组位置,用最小二乘法拟合两直线,得到相应的直线方程为:

两个区间的剩余平方和 (E=E1+E2)为1.037,以上两个方程都通过了显著性检验,其分界点 =11,r(11)=117.43。因此得出 Zn元素的异常下限为 117.43×10-6。

3 讨论

(1)传统地球化学方法所确定的异常下限值与含量-面积分形法所确定的异常下限有一定的偏差,出现偏差的原因是由于传统的算法本身缺陷所造成的,特别是在处理数据过程时,人为的剔除特高值。

(2)含量-面积分形计算方法的理论基础是地球化学数据服从分形分布,更能体现地球化学数据原始特征。

(3)为使含量-面积分形法所计算的结果更加精确,在估计的拐点两侧可适当加密分类的面积数。

图 2 江西永平地区 Zn元素地球化学等值线图① 所有样品由江西省地矿局实验测试中心(国家级)分析测试。Fig.2 The geochem ical contour line m ap of YongPing,J iangXi

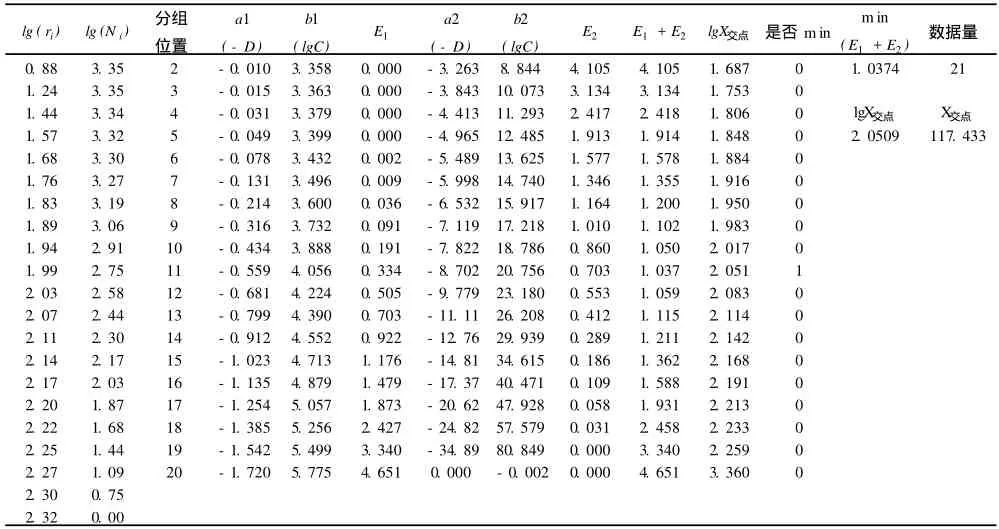
表2 分形计算结果表Tab.2 The object list of fractal

李长江.1999.麻土华.矿产勘查中的分形、混沌与 ANN[M].北京:地质出版社:1-140.

谢淑云,鲍征宇.2003.多重分形与地球化学元素的分布规律[J].地质地球化学,31(3):97-102.

Allegre C J,Lwein E.1995.Scaling laws and geochemical distributions[J].Earth and PlanetaryLetters,132:1-13.

Turcotte D L.1986.A fractal approach to the relationship between ore grade and tonnage[J].Economic Geology,(81):1528-1532.

Anomaly Threshold of Geochem istry Usi ng theMethod of Fractal
Content-Area:A Case Study i n Yongping,Jiangxi Province

HU Qing-hua, XI AO Xiao-lin, CAO Sheng-hua, WU Ming-ren, FENG Guo-sheng, XI ONGWei
(Jiangxi Institute of Geological Survey,Nanchang,JX 330030,China)

The anomaly threshold of geochemistry element is one of important problems of geochemistry research.The traditionalmethod only thinks about the randomness of data.However,the self-similarity and randomness are poor considered.In this study,the anomaly thresholds of geochemistry element are studied using content-area of fractal theory.The results bet ween this study and traditionalmethod show thismethod hasmore theory basis and practicality and the recognition accuracy of geochemical anomaly can be improved greatly.

fractal;anomaly threshold;geochemistry;the method of content-area

P595

A

1674-3504(2011)02-107-04

10.3969/j.issn.1674-3504.2011.02.002

2010-06-13

中国地质调查局矿产远景调查项目 (2005-13-10)

胡青华 (1979—),男,主要从事质矿产调查工作。E-mail:hu99111@163.com